Students can go through AP Board 6th Class Maths Notes Chapter 3 HCF and LCM to understand and remember the concepts easily.
AP State Board Syllabus 6th Class Maths Notes Chapter 3 HCF and LCM
→ Divisibility Rules:
A divisibility rule is a process by which we can determine whether a given number is completely divisible by other given number or not without performing actual division.
Reasons behind the rules:
Our number system is based on base 10 system. Every place value increases by 10-times as move from right to left.

→ Divisibility rule for 2: In the above place value table except ones place all other places namely 100/1000/10 000…. are completely divisible by 2. So for divisibility by 2 we need to check the unit digit only.
A number is divisible by 2 if it has any of the digits 0, 2, 4 or 8 in its units place.
In other words all even numbers are divisible by 2.
![]()
→ Divisibility rule for 3:
10/3 → not divisible
100/3 → not divisible
1000/3 → not divisible and it goes on..
But in all the cases, the remainder is 1. As such if the number 56817 is divided by 3 we get remainder, 5, 6, 8, 1 and 7 respectively. The sum of these remainders 5 + 6 + 8 + 1 + 7 = 27 is divisible by 3 as is the number is divisible by 3.
In other words if the sum of the digits of a given number is divisible by 3, then the given number is also divisible by 3.
The digital root of natural number is the single digit value obtained by repeated process of summing digits.
Example: The digital root of 325698 is 3 + 2 + 5 + 6 + 9 + 8 = 33 = 3 + 3 = 6
Note: While adding the digits of a number we can ignore 9’s or combinations of digits summing up to 9.
Example: The digital root of 87459634572 is
By dropping (4+5), (9), (6+3), (4+5), (7+2), the remaining digits are 8 & 7. From these digits eliminate 9 that is 8 + 7 – 9 = 15 – 9 = 6
Therefore the digital root of 87459634572 is 6. Hence divisible by 3.
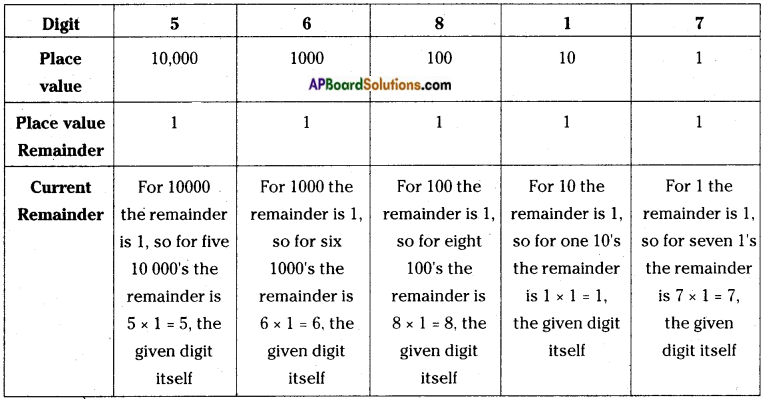
Now add these digits to get the total remainder. If this remainder is completely divisible by 3, then the given number is also divisible by 3.
Divisibility rule of 3 will add the digits and then check if its divisible by 3. This is applicable for numbers which leaves remainder 1 when 10 is divided by that number.
![]()
→ Divisibility rule for 4: In the place value table starting from 100, all other higher places namely 1000/10 000/100 000, …etc. are all completely divisible by 4. So we need to check the digits in ten’s and unit’s place for divisibility by 4.
A number is divisible by 4 if the number formed by the digits in its ten’s place and unit’s place taken in the same order is divisible by 4 and also zeros on both places.
Example: Is the number 87534 divisible by 4?
Number formed by last two digits 34 is not divisible by 4 and hence the given number is also not divisible by 4.
Example : Is the number 779956 divisible by 4?
Number formed by last two digits 56 is divisible by 4 and hence the given number is also divisible by 4.
→ Divisibility rule for 5: In the place value table starting from 10, all other higher places namely 10/100/1000/10000/1 00 000, ..’etc. are all completely divisible by 5. So we need to check the digits in unit’s place for divisibility by 5.
A number is divisible by 5 if the number ends in either zero of 5.
Example: Is the number 779956 divisible 5?
The digit in unit’s place is 6, so it is not divisible by 5.
Example: Is the number 77995 divisible by 5?
The digit in unit’s place is 5, so it is divisible by 5.
Example: Is the number 779950 divisible by 5?
The digit in unit’s place is 0, so it is divisible by 5.
→ Divisibility rule for 6 : If a number is divisible by both 2 and 3, then it is also divisible by 6.
Example: Is the number 612432 divisible by 6?
As the given number is an even number it is divisible by 2.
Also the digital root of the number is 3, it is divisible by 6.
Hence it is divisible by 6.
In other words if a number is divisible by two relatively prime numbers, then their product also divides the given number.
![]()
→ Divisibility rule for 8: In the place value table starting from 1000, all other higher places namely 10 000/1 00 000…etc., are all completely divisible by 8. So we need to check the digits in hundred’s, ten’s and unit’s place for divisibility by 8.
A number is divisible by 8 if the number formed by the digits in its hundred’s place, ten’s place and unit’s place taken in the same order is divisible by 8, are also zeros on three places.
Example: Is the number 875344 divisible by 8?
Number formed by last three digits 344 is divisible by 8 and hence the given number is also divisible by 8.
→ Divisibility rule for 9: The rule is same as rule for 3
10/9 → not divisible
100/9 → not. divisible
1000/9 → not divisible and it goes on ..
But in all the cases, the remainder is 1. As such if the number 56817 is divided by 9 we get remainder, 5, 6, 8, 1 and 7 respectively. The sum of these remainders 5 + 6 + 8 + 1 + 7 = 27 is divisible by 9 as is the number is divisible by 3.
In other words if the sum of the digits of a given number is divisible by 9, then the given number is also divisible by 9.
The digital root of natural number is the single digit value obtained by repeated process of summing digits.
Example: The digital root of 325698 is 3 + 2 + 5 + 6 + 9 + 8 = 33 = 3 + 3 = 6
Note: While adding the digits of a number we can ignore 9’s or combinations of digits summing up to 9.
Example: Is the number 7854963 divisible by 9?
The digital root of the given number is 7 + 8 + 5 + 4 + 9 + 6 + 3 = 42 = 4 + 2 = 6, not divisible by 9.
![]()
→ Divisibility rule for 10: In the place value table starting from 10, all other higher places namely 10/100/1000/10000/100000…etc., are all completely divisible by 10. So we need to check the digits in unit’s place for divisibility by 10.
A number is divisible by 10 if the number ends in zero.
Example: Is the number 779956 divisible 10?
The digit in unit’s place is 6, so it is not divisible by 10.
Example: Is the number 779950 divisible 10?
The digit in unit’s place is 0, so it is divisible by 10.
→ Divisibility rule for 11: A number is divisible by 11, if the difference between the sum of digits at even places and the sum of digits at odd place is either zero or a multiple of 11.
Example: Is the number 52487 divisible 11?
Sum of the digits at odd places = 7 + 4 + 5 = 16 Sum of the digits at even places = 8 + 2 = 10 Difference = 16 – 10 = 6, not divisible by 11.
Note: If two numbers are divisible by a given number, then their sum, difference and the product are also divisible by that number.
→ Factor: A factor of a number is an exact divisor of that number.
Example: 15 = 5 × 3, here 5 divides 15 completely and 3 divides 15 completely. As such 1, 3, 5, 15 are factors of 15.
Also 15 = 1 × 15. It means 1 is a factor of every number and every number is a factor of itself.
Every factor of a number is less than or equal to the number.
Perfect number: A number for which the sum of all its factors is equal to twice the number is called a perfect number.
Example: 6 = 1 × 6
= 2 × 3, here 1, 2,3 and 6 are factors whose sum is (1 + 2 + 3 + 6 = 12) 12, twice the given number 6. So 6 is a perfect number.
6, 28, 496, 8128…… are perfect numbers. Euclid has given a formula to derive perfect
numbers.
If q is a prime of the form 2p – 1 where p is a prime, then q(q+1)/2 is an even perfect number.
→ Multiple: Multiples of a given number can be obtained by multiplying the given number with natural numbers i.e. 1, 2, 3, 4, …. etc.
Example: Multiple of 6 are:
= 6 × 1, 6 × 2, 6 × 3, 6 × 4, …..
= 6, 12, 18, 24, …..
![]()
→ Prime number: Numbers having only two factors namely one and itself are called prime numbers.
A prime number is a whole number that has exactly two factors, 1 and itself.
Example: 2, 3, 5, 7, 11,
All the above numbers have only two factors namely 1 and itself.
We can write infinitely many prime numbers.
2 is the only even prime number. Also 2 is the smallest prime number.
→ Composite number: Numbers having more than two factors are called composite numbers.
Example: 4, 6, 8, 9, ….
1 is neither a prime number nor a composite number.
The Sieve of Eratosthenes is an ancient algorithm that can help us find all prime numbers up to any given limit.
→ How does the Sieve of Eratosthenes work?
The following example illustrates how the Sieve of Eratosthenes, can be used to find all the prime numbers that are less than 100.
Step 1: Write the numbers from 1. to 100 in ten rows as shown below.
Step 2: Cross out 1 as 1 is neither a prime nor a composite number.
Step 3: Circle 2 and cross out all the multiples of 2. (2, 4, 6, 8, 10, 12, ….)
Step 4: Circle 3 and cross out all the multiples of 3. (3, 6, 9, 12, 15, 18, ….)
Step 5: Circle 5 and cross out all the multiples of 5. (5, 10. 15, 20, 25, ….)
Step 6: Circle 7 and cross out all multiples of 7. (7, 14, 21. 28, 35, ….)
Circle all the numbers that are not crossed out and they are the required prime numbers less than 100.

Alternate method:
Finding prime numbers upto 100
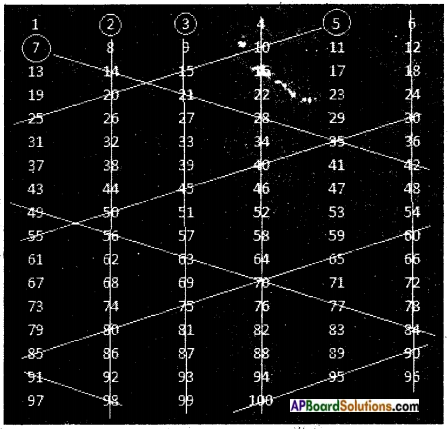
First arrange the numbers from 1 to 100 in a table as shown above.
Enter 6 numbers in each row until the last number 100 is reached.
First we select a number and we strike off all the multiples of it.
Start with 2 which is greater than 1.
Round off number 2 and strike off entire column until the end.
Similarly strike off 4th column and 6th column as they are divisible by 2.
Now round off next number 3 and strike off entire column until end.
The number 4 is already gone.
Now round off next number 5 and strike off numbers in inclined fashion as shown in the figure (they are all divisible by 5). When striking off ends in some row, start again striking off with number in another end which is divisible by 5. New striking off line should be parallel to previous strike off line as. shown in the figure.
The number 6 is already gone.
Now round off number 7 and strike off numbers as we did in case of number 5.
8,9,10 are also gone.
Stop at this point.
Count all remaining numbers. Answer will be 25.
![]()
→ Prime numbers
There are 25 prime numbers less than 100.
These are:

What if we go above 100? Around 400 BC the Greek mathematician. Euclid, proved that there are infinitely many prime numbers.
→ Co-primes: Two numbers are said to be co-prime if they have no factors in common. Example: (2, 9), (25, 28)
Any two consecutive numbers always form a pair of co-prime numbers.
Example: (7 & 8), (21 & 22), …..
Co-prime numbers are also called relatively prime number to one another.
Example: 3, 5, 8, 47 are relatively prime to one another/co-prime to each other.
→ Twin primes: Two prime numbers are said to be twin primes, if they differ by 2. Example: (3, 5), (5, 7), (11, 13), …etc.
→ Prime factorization: The process of expressing the given number as the product of prime numbers is called prime factorization.
Example: Prime factorization of 24 is
24 = 2 × 12 = 2 × 2 × 6
= 2 × 2 × 2 × 3, this way is unique.
Every number can be expressed as product of primes in a unique manner. We can factorize a given number in to product of primes in two methods. They are
a) Division method
b) Factor tree method
![]()
→ Common factors: The set of all factors which divides all the given numbers are called their common factors.
Example: Common factors to 24, 36 & 48 are 1, 2, 3, 4, 6 & 12
Factors of 24 = 1, 2, 3, 4, 6, 8, 12 & 24
Factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18 & 36
Factors of 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24 & 48
Common factors to 24, 36 & 48 are 1, 2, 3, 4, 6 & 12
We can see that among their common factors 12 is the highest common factor. It is called H.C.F. of the given numbers. So H.C.F. of 24, 36 & 48 is 12.
→ H.C.F./G.C.D : The highest common factor or the greatest common divisor of given numbers is the greatest of their common factors.
H.C.F. of given two or more numbers can be found in two ways.
a) By prime factorization
b) By continued division
H.C.F. of any two consecutive numbers is always 1.
H.C.F. of relatively prime/co-prime numbers is always 1.
H.C.F. of any two consecutive even numbers is always 2.
H.C.F. of any two consecutive odd numbers is always 1.
→ Common multiples:
Multiples of 8: 8, 16, 24, 32, 40, 48, ….
Multiples of 12: 12, 24, 36, 48, ….
Multiples.common to 8 & 12: 24, 48; 72, 96, ….
Least among the common multiple is 24. This is called L.C.M. of 8 & 12. The number of common multiples of given two or more numbers is infinite, as such greatest common multiple cannot be determined.
→ L.C.M.: The least common multiple of two or more numbers is the smallest natural number among their common multiples.
L.C.M. of given numbers can be found by the
a) Method of prime factorization.
b) Division method.
L.C.M. of any two consecutive numbers is always equal to their product.
L.C.M. of 8 & 9 is 8 × 9 = 72
L.C.M. of co-prime numbers is always equal to their product.
L.C.M. of 8 & 15 is 8 × 15 = 120
![]()
→ Relation between the L.C.M. & H.C.F:
For a given two numbers N1 & N2, the product of the numbers is equal to the product of their L.C.M.(L) & H.C.F.(H)
N1 × N2 = L × H