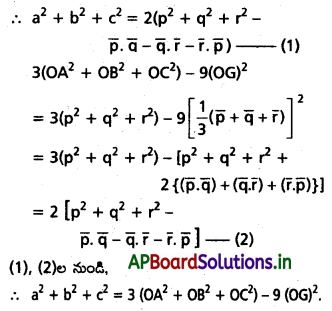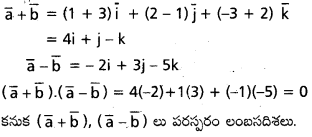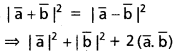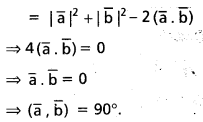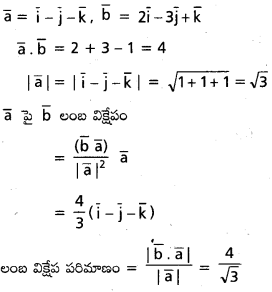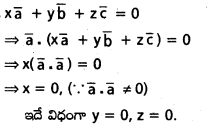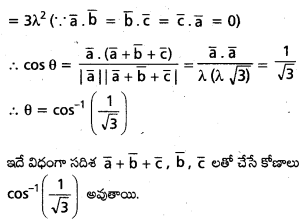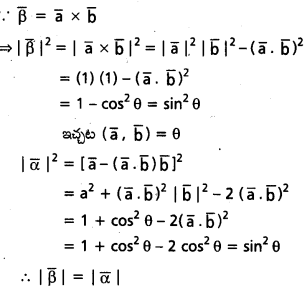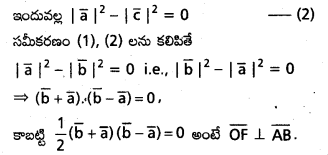Students get through AP Inter 1st Year Maths 1A Important Questions Chapter 4 సదిశల సంకలనం which are most likely to be asked in the exam.
AP Inter 1st Year Maths 1A Important Questions Chapter 4 సదిశల సంకలనం
సాధించిన సమస్యలు
(Solved Problems)
ప్రశ్న 1.
సదిశ a = 2i + 3j + k దిశలో యూనిట్ సదిశను కనుక్కోండి. [Mar. ’14]
సాధన:
సదిశ a దిశలో యూనిట్ సదిశను \(\hat{a}=\frac{1}{|a|}\) a గా తెలపగలం.
|a| = \(\sqrt{2^2+3^2+1^2}=\sqrt{14}\)
కాబట్టి \(\hat{a}=\frac{1}{\sqrt{14}}\) (2i + 3j + k)
= \(\frac{2}{\sqrt{14}}\)i + \(\frac{3}{\sqrt{14}}\)j + \(\frac{1}{\sqrt{14}}\)k
ప్రశ్న 2.
సదిశ a = j – 2j దిశలో 7 యూనిట్ల పరిమాణం గలిగిన ఒక సదిశను కనుక్కోండి.
సాధన:
సదిశ a దిశలో యూనిట్ సదిశ
â \(=\frac{1}{a}\)a = \(\frac{1}{\sqrt{5}}\)(i – 2j) = \(\frac{1}{\sqrt{5}}\)i – \(\frac{2}{\sqrt{5}}\)j
కాబట్టి a దిశలో 7కి సమానమయ్యే పరిమాణం గలిగిన సదిశ
7a = 7\(\left(\frac{1}{\sqrt{5}} i-\frac{2}{\sqrt{5}} j\right)\) = \(\frac{7}{\sqrt{5}} \mathrm{i}-\frac{14}{\sqrt{5}} \mathrm{j}\)
![]()
ప్రశ్న 3.
a = 2i + 2j – 5k, b = 2i + j + 3k సదిశల సంకలన దిశలోని యూనిట్ సదిశను కనుక్కోండి. [May ’13]
సాధన:
దత్త సదిశల మొత్తం a + b (= c అనుకొంటే).
= 4i + 3j – 2k.
|c| = \(\sqrt{4^2+3^2+(-2)^2}\)
= \(\sqrt{29}\)
∴ ĉ = \(\frac{\overline{4}+\overline{3 j}-2 \hat{k}}{\sqrt{29}}\)
ప్రశ్న 4.
సదిశ a = i + j – 2k యొక్క దిక్ నిష్పత్తులను రాసి, తద్వారా దిక్ కొసైన్లను గణన చేయండి.
సాధన:
సదిశ r = xi + yj + zk యొక్క దిక్ నిష్పత్తులు a, b, c వరసగా ఆసదిశ అంశలు X. y, Z లు అవుతాయని గమనించండి.
కాబట్టి, దత్త సదిశకి a = 1, b = 1, c = -2,
అంతేకాక దత్త సదిశకు l, m, n దిక్ కొసైన్లు అయితే,
|r| = \(\sqrt{6}\) అయితే l = \(\frac{a}{|r|}=\frac{1}{\sqrt{6}}\)
m = \(\frac{b}{|r|}=\frac{1}{\sqrt{6}}\)
n = \(\frac{c}{|r|}=\frac{1}{\sqrt{6}}\)
∴ a దిక్ కొసైన్లు \(\left(\frac{1}{\sqrt{6}}, \frac{1}{\sqrt{6}},-\frac{2}{\sqrt{6}}\right)\)
ప్రశ్న 5.
స్థాన సదిశలను OP = 3a – 2b, OQ = a + bగా గలిగిన రెండు బిందువులు P, Qలను తీసుకోండి. P, Q లను కలిపే సరళరేఖను 2:1 నిష్పత్తిలో (i) అంతరంగాను (ii) బాహ్యంగాను విభజించే బిందువు R స్థాన సదిశను కనుక్కోండి.
సాధన:
i) P, Q లను కలపే సరళరేఖను 2:1 నిష్పత్తిలో అంతరంగా విభజించే బిందువు R స్థాన సదిశ
OR = \(\frac{2(a+b)+(3 a-2 b)}{2+1}=\frac{5 a}{3}\)
ii) P, Q లను కలిపే సరళరేఖను 2 1 నిష్పత్తిలో బాహ్యంగా విభజించే బిందువు R స్థాన సదిశ
OR = \(\frac{2(a+b)-(3 a-2 b)}{2-1}\)
= 4b – a.
![]()
ప్రశ్న 6.
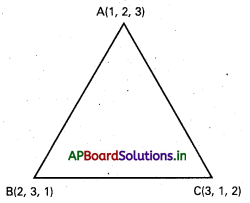
A(2i – j + k), B(i – 3j – 5k), C(3i – 4j – 4k) బిందువులు ఒక లంబకోణ త్రిభుజం శీర్షాలని చూపండి.
సాధన:
AB = (1 – 2)i + (−3 + 1)j + (-5-1)k
= -i – 2j – 6k.
BC = (3 – 1)i + (-4 + 3)j + (-4 + 5)k
= 2i – j + k
CA = (2 – 3)i + (-1 + 4)j + (1 + 4)k
= i + 3j + 5k.
దీనితో |AB|2 = BC|2 + |CA|2.
ప్రశ్న 7.
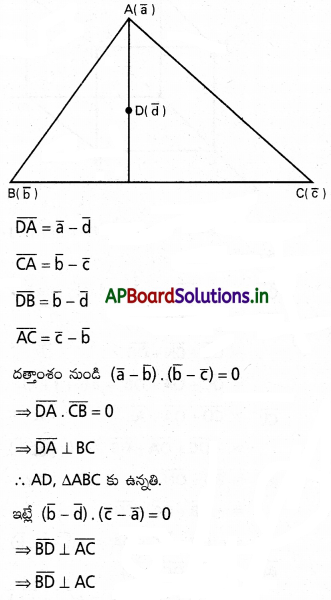
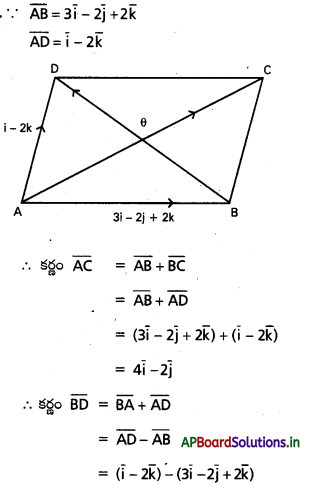
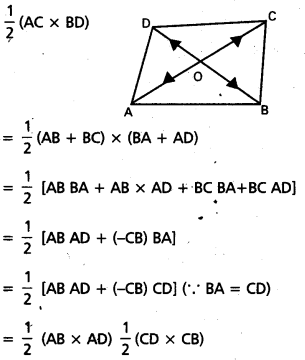
A, B, C, D బిందువుల స్థాన సదిశలు వరుసగా \(\overline{\mathrm{a}}+2 \overline{\mathrm{b}}, 2 \overline{\mathrm{a}}-\overline{\mathrm{b}}, \overline{\mathrm{a}}, 3 \overline{\mathrm{a}}+\overline{\mathrm{b}}\) అయితే \(\overline{\mathrm{A C}}, \overline{\mathrm{DA}}, \overline{\mathrm{BA}}, \overline{\mathrm{B C}}\) సదిశలను a, bలలో రాయండి.
సాధన:
A, B, C, D బిందువుల స్థాన సదిశలు దృష్ట్యా

ప్రశ్న 8.
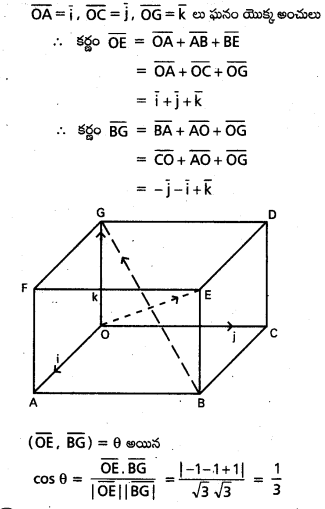
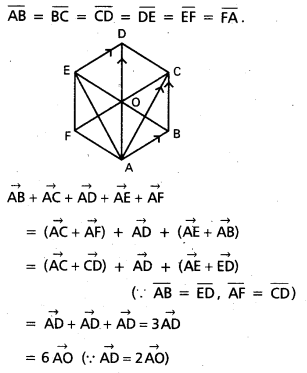
ABCDEF క్రమ షడ్భుజి కేంద్రం ‘0’ అయితే \(\overline{\mathrm{AB}}+\overline{\mathrm{AC}}+\overline{\mathrm{AD}}+\overline{\mathrm{AE}}+\overline{\mathrm{AF}}=3 \overline{\mathrm{AD}}=6 \overline{\mathrm{AO}}\) అని చూపండి. [(A.P) Mar. ’15]
సాధన:
ABCDEF క్రమషడ్భుజి, కేంద్రం ‘0’.
![]()
ప్రశ్న 9.
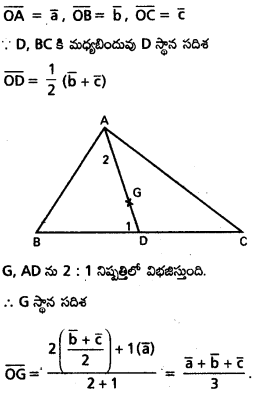
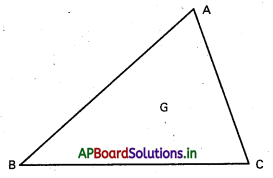
∆ABC త్రిభుజంలో A, B, C ల స్థాన సదిశలు వరుసగా \(\overline{\mathrm{a}}, \overline{\mathrm{b}}, \overline{\mathrm{c}}\) అయితే, దాని కేంద్రభాసం (centroid) స్థాన సదిశ \(\frac{1}{3}(\overline{\mathrm{a}}, \overline{\mathrm{b}}, \overline{\mathrm{c}})\) అని చూపండి.
సాధన:
∆ABC లో G కేంద్రభాసం శీర్షం A గుండా గీచిన మధ్యగత
రేఖ AD. అప్పుడు
AG : GD ≠ 2 : 1. ‘O’ మూలబిందువు
![]()
ప్రశ్న 10.
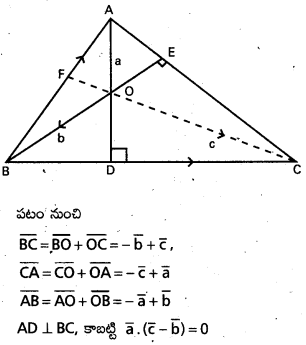
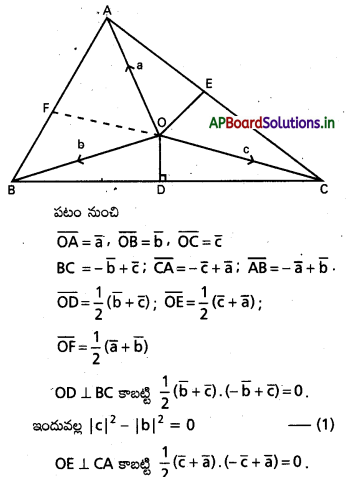
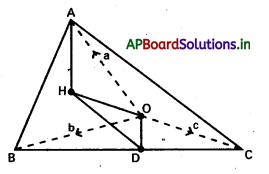
∆ABC లో ‘O’ పరివృత్త కేంద్రం, H లంబ కేంద్రం అయితే
i) \(\overline{\mathrm{OA}}+\overline{\mathrm{OB}}+\overline{\mathrm{OC}}=\overline{\mathrm{OH}}\)
ii) \(\overline{\mathrm{HA}}+\overline{\mathrm{HB}}+\overline{\mathrm{HC}}=2 \overline{\mathrm{HO}}\) అని చూపండి.
సాధన:
BC మధ్యబిందువు D అనుకుందాం.
i) ‘O’ మూలబిందువు \(\overline{O A}=\overline{a}\), \(\overline{O B}=\overline{b}\), \(\overline{O C}=\overline{c}\) అనుకుందాం.

ప్రశ్న 11.
ఒక చతుర్ముఖి శీర్షాలు A, B, C, D. వీటి స్థాన సదిశలు క్రమంగా \(\overline{\mathrm{a}}, \overline{\mathrm{b}}, \overline{\mathrm{c}}, \overline{\mathrm{d}}\) అయితే, ఆ శీర్షాలను ఎదుటి ముఖాల కేంద్ర భాసాలకు కలిపే రేఖలు అనుషక్తాలవుతాయని చూపండి. (ఈ బిందువును చతుర్ముఖి కేంద్రభాసం లేదా కేంద్రం అంటారు). [(A.P)
సాధన:
‘O’ మూలబిందువు.
G1, G2, G3, G4 లు వరుసగా
∆BCD, ∆CAD, ∆ABD, ∆ABC ల కేంద్రభాసాలు
∴ OG1 = \(\frac{\overline{b}+\vec{c}+\overline{d}}{3}\)
AG1 ను 3: 1 నిష్పత్తిలో విభజించే బిందువు P అనుకొందాం.
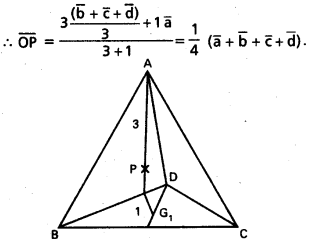
ఇదే విధంగా BG2, CG3, DG4, 3 : 1 అను నిష్పత్తిలో విభజించే బిందువుల స్థాన సదిశలు \(\frac{1}{4}(\overline{a}+\overline{b}+\overline{c}+\overline{d})\). కాబట్టి P బిందువు AG1, BG2, CG3, DG4 లలో ప్రతి దానిపై ఉంటుంది.
![]()
ప్రశ్న 12.
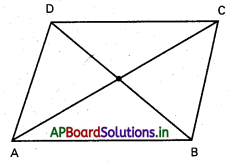
OABC సమాంతర చతుర్భుజంలో OA మధ్య బిందువు D అయితే, CD రేఖాఖండం కర్ణం OB పరస్పరం త్రిధాకరించుకొంటాయని చూపండి.
సాధన:
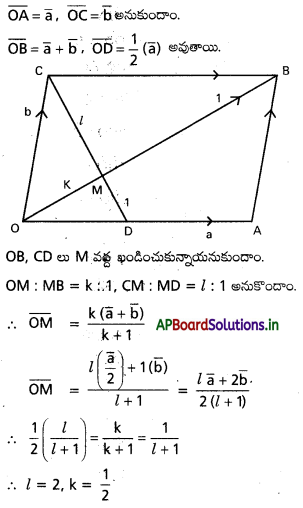
కాబట్టి CD, OB ని OB, CD ని త్రిధాకరించుకుంటాయి.
ప్రశ్న 13.
\(\overline{\mathrm{a}}, \overline{\mathrm{b}}\) లు సరేఖీయాలు కాని సదిశలు. \(\mathrm{3} \overline{\alpha}=\mathrm{2} \overline{\beta}\) అయ్యేటట్లు
\(\overline{\alpha}\) = (x + 4y) \(\overline{\mathrm{a}}\) + (2x + y + 1)\(\overline{\mathrm{b}}\),
\(\overline{\beta}\) = (y – 2x + 2) \(\overline{\mathrm{a}}\) + (2x – 3y – 1) \(\overline{\mathrm{a}}\), ఉంటే x, yలను కనుక్కోండి.
సాధన:
\(\mathrm{3} \overline{\alpha}=\mathrm{2} \overline{\beta}\)
⇒ 3(x + 4y) \(\overline{\mathrm{a}}\) + 3 (2x + y + 1)\(\overline{\mathrm{b}}\) = 2(y – 2x + 2)\(\overline{\mathrm{a}}\) (2x – 3y – 1)\(\overline{\mathrm{b}}\)
\(\overline{\mathrm{a}}, \overline{\mathrm{b}}\) గుణకాలను సమానం చేస్తే
3x + 12y = 2y – 4x + 4
⇒ 7x + 10y = 4 ………………… (1)
6x + 3y + 3 = 4x – 6y – 2
⇒ 2x + 9y = -5 ……………….. (2)
(1), (2) ల నుండి..
x = 2, y = -1
![]()
ప్రశ్న 14.
\(\overline{\mathrm{a}}, \overline{\mathrm{b}}, \overline{\mathrm{c}}\) లు అతలీయ సదిశలైతే \(-2 \overline{a}+3 \overline{\mathrm{b}}+5 \overline{c},\overline{\mathrm{a}}+\mathrm{2 \overline { b }}+3 \overline{\mathrm{c}}, 7 \overline{\mathrm{a}}-\overline{\mathrm{c}}\) బిందువులు సరేఖీయాలని చూపండి.
సాధన:
మూలబిందువు. P, Q. Rలు దత్త బిందువులు అనుకుందాం.

⇒ P, Q, R లు సరేఖీయాలు.
![]()
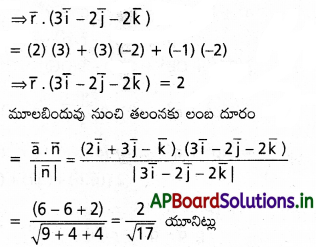
ప్రశ్న 15.
\(3 \overline{\mathrm{i}}-2 \overline{\mathrm{j}}-\overline{\mathrm{k}}, \mathrm{2} \overline{\mathrm{i}}+3 \overline{\mathrm{j}}-4 \overline{\mathrm{k}},-\overline{\mathrm{i}}+\overline{\mathrm{j}}+2 \overline{\mathrm{k}}\), \(\mathrm{4} \overline{\mathrm{i}}+\mathrm{5} \overline{\mathrm{j}}+\lambda \overline{\mathrm{k}}\) సదిశలను స్థాన సదిశలుగా గల బిందువులు సతలీయాలైతే λ విలువ \(\frac{-146}{7}\) అని చూపండి.
సాధన:
‘O’ మూలబిందువు, A, B, C, D లు దత్త బిందువులు.

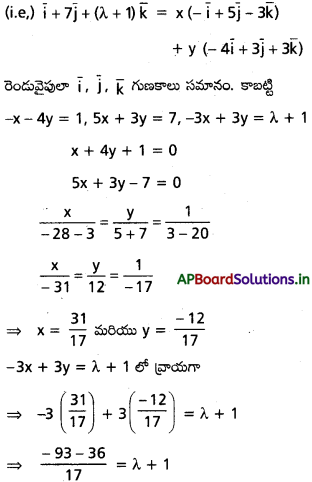
∴ λ = -1 – \(\frac{129}{17}\)
⇒ λ = \(\frac{-17-129}{17}\) = \(\frac{-146}{17}\)
![]()
ప్రశ్న 16.
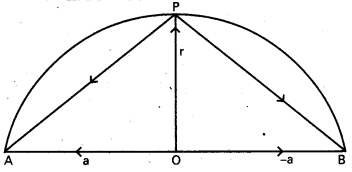
ద్విపరిమాణ నిరూపక తలంలో, సదిశా పద్ధతులనుప యోగించి, నిరూపకాక్షాల మీద ‘a’, ‘b’ అంతర ఖండాలు చేసే రేఖ సమీకరణం \(\frac{x}{a}+\frac{y}{b}\) = 1 అవుతుందని రుజువు చూపండి.
సాధన:
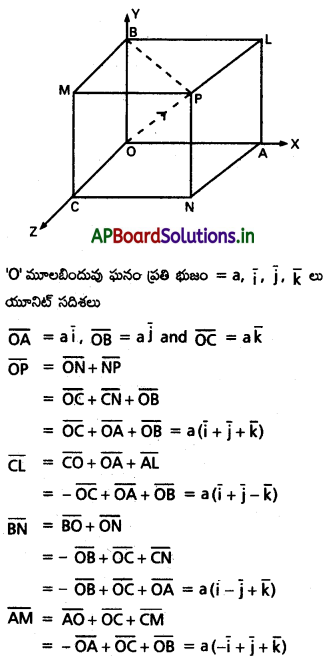
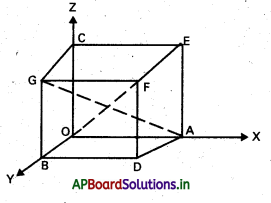
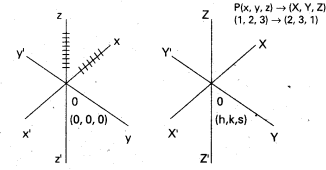
OXYZ ద్విపరిమాణ నిరూపక తలం.
\(\overline{\mathrm{i}}, \overline{\mathrm{j}}\) లు వరుసగా ధన x, y అక్షాల మీద యూనిట్ సదిశలు.
\(\overline{a}=a \overline{i}, \overline{b}=b \overline{j}\)
మూలబిందువు. \(\overline{\mathrm{OA}}={\mathrm{a}}, \overline{\mathrm{OB}}=\overline{\mathrm{b}}\) అయ్యేటట్లుగా
A, B లు తలం మీద రెండు బిందువులు,
\(\overline{\mathrm{AB}}\) రేఖా సదిశా సమీకరణం
\(\overline{r}=(1-t)^{a \overline{i}+t-b \overline{j}}\)
\(\overline{r}=x \overline{i}+y \overline{j}\) అయితే,
అపుడు x = (1 – t) a, y = t b
‘t’ ను తొలగింపని x = \(\left(1-\frac{y}{b}\right)\)a
⇒ \(\frac{x}{a}\) = 1 – \(\frac{y}{b}\)
⇒ \(\frac{x}{a}+\frac{y}{b}\) = 1
ప్రశ్న 17.
రెండు బిందువులగుండా పోయే సరళరేఖ సదిశా సమీకరణాన్ని ఉపయోగించి, \(\overline{\mathrm{a}}, \overline{\mathrm{b}},(3 \overline{\mathrm{a}}-\mathrm{2} \overline{\mathrm{b}})\) లను స్థాన సదిశలుగా గల బిందువులు సరేఖీయాలని రుజువు చేయండి.
సాధన:
\(\overline{a}, \overline{b}\) ల గుండా పోయే సరళరేఖా సదిశాసమీకరణం
\(\overline{r}=(1-t) \overline{a}+t \overline{b}\) ; t ∈ R
ఈ రేఖ గుండా బిందువు \(3 \overline{a}-2 \overline{b}\) పోతే
\(3 \overline{a}-2 \overline{b}=(1-t) \overline{a}+t \overline{b}\)
అనురూప గుణకాల సమానం చేయగా
1 – t = 3, t = -2
దత్త బిందువులు సరేఖీయాలు.
![]()
ప్రశ్న 18.
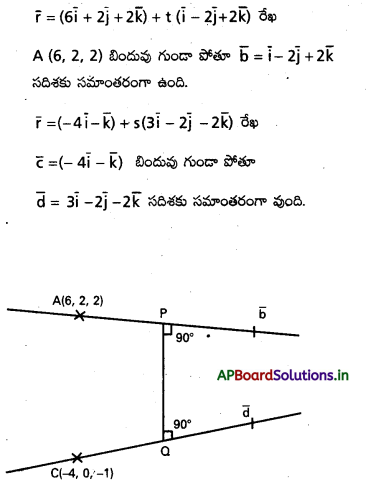
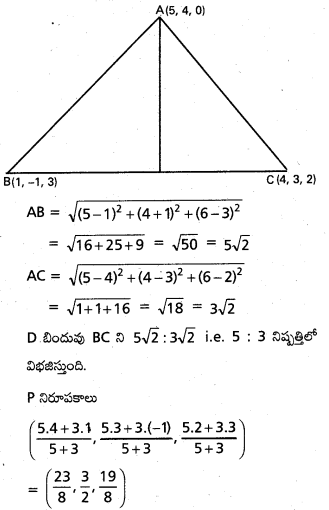
\(\mathrm{2} \overline{\mathrm{i}}-\overline{\mathrm{j}}+\mathrm{2} \overline{\mathrm{k}}\) సదిశకు సమాంతరంగా ఉంటూ, \(({3} \overline{\mathrm{i}}+\overline{\mathrm{j}}-\overline{\mathrm{k}})\) ని స్థాన సదిశగా గలిగిన బిందువు A గుండా పోయే రేఖ సదిశా సమీకరణాన్ని కనుక్కోండి. AP = 15 అయ్యేటట్లు ఈ రేఖమీద P అనే బిందువు ఉండే, P స్థాన సదిశ కనుక్కోండి.
సాధన:
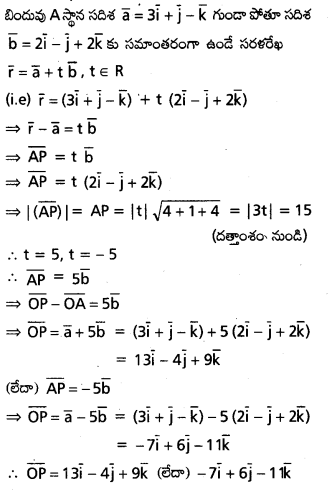
![]()
ప్రశ్న 19.
\(\overline{\mathrm{a}}, \overline{\mathrm{b}}, \overline{\mathrm{c}}\) లు అతలీయ సదిశలైతే, \(6 \bar{a}-4 \bar{b}+4 \bar{c},-4 \bar{c}\) బిందువులు కలిపే రేఖలు \(-\overline{\mathrm{a}}-2 \bar{b}-3 \bar{c}, \bar{a}+2 \bar{b}-5 \bar{c}\) బిందువులను కలిపే రేఖల ఖండన బిందువు \(-4 \bar{c}\) అని చూపండి.
సాధన:
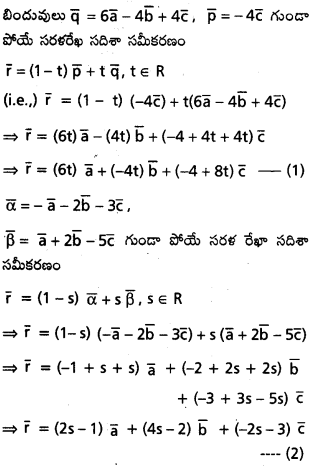
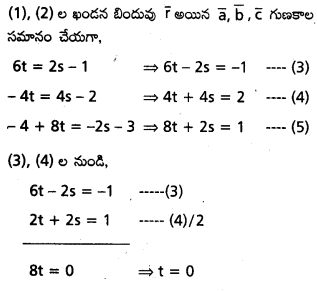
(1) నుండి, S = \(\frac{1}{2}\)
t = 0, s = \(\frac{1}{2}\) లను (5)లో వ్రాస్తే,
8(0) + 2(\(\frac{1}{2}\)) =1 ⇒ 1 = 1
(1), (2) రేఖలు ఖండించుకొంటాయి.
ఖండన బిందువుల కొరకు t = 0 ను (1) లో వ్రాస్తే
\(\overline{\mathrm{r}}=-4 \overline{\mathrm{c}}\)
∴ రేఖల ఖండన బిందువు స్థాన సదిశ \(-4 \bar{c}\).
![]()
ప్రశ్న 20.
\(\overline{\mathrm{a}}, \overline{\mathrm{b}}, \overline{\mathrm{c}}\) లు అతలీయ సదిశలైతే, సరళరేఖ \(\overline{\mathrm{r}}=2 \overline{\mathrm{a}}+\overline{\mathrm{b}}+t(\overline{\mathrm{b}}-\overline{\mathrm{c}})\), తలం \(\overline{\mathrm{r}}=\overline{\mathrm{a}}+x(\bar{b}+\bar{c})+y(\bar{a}+2 \bar{b}-\bar{c})\)ని ఖండించే బిందువును కనుక్కోండి. [May ’13]
సాధన:
రేఖా తలంలో ఖండన బిందువు P, దాని స్థాన సదిశ \(\bar{r}\) అయిన
\(2 \bar{a}+\bar{b}+t(\bar{b}-\bar{c})=\bar{a}+x(\bar{b}+\bar{c})+y(\bar{a}+2 \bar{b}-\bar{c})\)
∴ \(\bar{a}, \bar{b}, \bar{c}\) కె.లు అతలీయ సదిశలు
కనుక \(\bar{a}, \bar{b}, \bar{c}\) గుణకాలను పోల్చగా,
2 = 1 + y ⇒ y = 1
1 + t = x + 2y
⇒ 1 + t = x + 2(1)
⇒ t – x = 1 ……………. (1)
-t = x – y
x + t = y
⇒ x + t = 1 ………….. (2)
(1), (2) ల నుండి, t = 1, x = 0, y = 1
∴ ఖండన బిందువు = \(\bar{r}=2 \bar{a}+\bar{b}+1(\bar{b}-\bar{c})\)
⇒ \(\overline{\mathrm{r}}=2 \overline{\mathrm{a}}+2 \overline{\mathrm{b}}-\overline{\mathrm{c}}\)
∴ ఖండన బిందువు స్థాన సదిశ\(2 \bar{a}+2 \bar{b}-\bar{c}\)

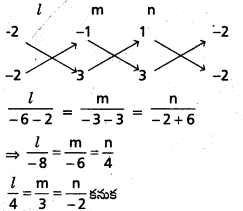
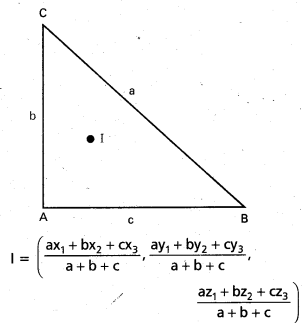

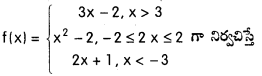

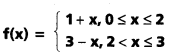 గానిర్వచిస్తే
గానిర్వచిస్తే