AP SCERT 6th Class Maths Textbook Solutions Chapter 11 చుట్టుకొలత – వైశాల్యం Unit Exercise Questions and Answers.
AP State Syllabus 6th Class Maths Solutions 11th Lesson చుట్టుకొలత – వైశాల్యం Unit Exercise
ప్రశ్న 1.
48 సెం.మీ. చుట్టుకొలతగల చతురస్ర వైశాల్యం కనుగొనండి.
సాధన.
చతురస్ర చుట్టుకొలత = 48 సెం.మీ.
4 × భుజం = 48 సెం.మీ.
భుజం = \(\frac {48}{4}\) = 12 సెం.మీ.
∴ చతురస్ర వైశాల్యం = భుజం × భుజం = 12 × 12 = 144 చ.సెం.మీ.
![]()
ప్రశ్న 2.
దీర్ఘచతురస్ర పొడవు 14 సెంటీమీటర్లు. దాని చుట్టుకొలత పొడవుకు 3రెట్లు. అయిన దాని వైశాల్యం కనుగొనండి.
సాధన.
దీర్ఘచతురస్ర పొడవు = 14 సెం.మీ.
దీర్ఘ చతురస్ర చుట్టుకొలత పొడవుకు 3 రెట్లు.
∴ దీర్ఘ చతురస్ర చుట్టుకొలత = 3 × 14 = 42 సెం.మీ.
2 × పొడవు + 2 × వెడల్పు = 42
2 × 14 + 2 × వెడల్పు = 42
28 + 2 × వెడల్పు = 42
2 × వెడల్పు = 42 – 28
2 × వెడల్పు = 14
వెడల్పు = \(\frac {14}{2}\) = 7 సెం.మీ.
∴ దీర్ఘ చతురస్ర వైశాల్యం = పొడవు × వెడల్పు = 14 × 7 = 98 చ|| సెం.మీ.
ప్రశ్న 3.
14 సెం.మీ. వ్యాసం గల వృత్త పరిధి కనుగొనండి.
సాధన.
వృత్త వ్యా సము = 14 సెం.మీ.
14. వృత్త వ్యాసార్ధము = \(\frac {14}{2}\) = 7 సెం.మీ.
వృత్త పరిధి = 2πr = 2 × \(\frac {22}{7}\) × 7 = 44 సెం.మీ.
![]()
ప్రశ్న 4.
దీర్ఘచతురస్ర పొడవు, వెడల్పులు వరుసగా 14 సెం.మీ., 12 సెంటీమీటర్లు. దాని వెడల్పు 6 సెం.మీ. పెంచి, పొడవు 6 సెం.మీ. తగ్గించిన, వైశాల్యంలో మార్పు కనుగొనండి.
సాధన.
దీర్ఘచతురస్ర పొడవు = 14 సెం.మీ.
వెడల్పు = 12 సెం.మీ.
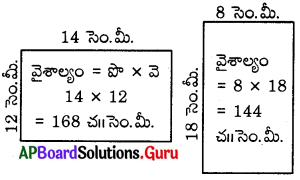
∴ దీర్ఘ చతురస్ర వైశాల్యం = పొడవు × వెడల్పు = 14 × 12 = 168 చ|| సెం.మీ.
పై దీర్ఘచతురస్ర వెడల్పు 6 సెం.మీ. పెంచి, పొడవు 6 సెం.మీ. తగ్గించినపుడు ఏర్పడు దీర్ఘచతురస్రపు
పొడవు = 14 – 6 = 8 సెం.మీ.
వెడల్పు = 12 + 6 = 18 సెం.మీ.
దీర్ఘ చతురస్ర వైశాల్యం = 8 × 18 = 144 చ|| సెం.మీ.
కొత్తగా ఏర్పడిన దీర్ఘచతురస్ర వైశాల్యం = 168 – 144 = 24 చ||సెం||మీ. తగ్గుతుంది.
ప్రశ్న 5.
కింది పటాల చుట్టుకొలతలు కనుగొనండి. ఏమి గమనించారు?
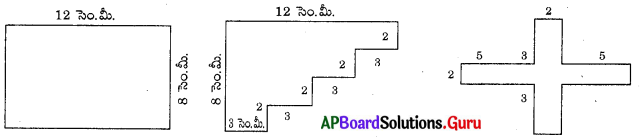
సాధన.
(i) దీర్ఘచతురస్ర పొడవు = 12 సెం.మీ., వెడల్పు = 8 సెం.మీ.
దీర్ఘచతురస్ర చుట్టుకొలత = 2 × పొడవు + 2 × వెడల్పు = 2 × 12 + 2 × 8 = 24 + 16 = 40 సెం.మీ.
(ii) చుట్టుకొలత = 12 + 8 + 3 + 2 + 3 + 2 + 3 + 2 + 3 + 2 = 40 సెం.మీ.
(iii) చుట్టుకొలత = 2 + 5 + 3 + 2 + 3 + 5 + 2 + 5 + 3 + 2 + 3 + 5 = 40 సెం.మీ.
గమనించిన అంశం : పై మూడు పటాల ఆకారాలు వేరుగా ఉన్న వాటి చుట్టుకొలతలు మాత్రం ఒకటే.
![]()
ప్రశ్న 6.
8 సెం.మీ. భుజం గల ఒక చతురస్రాకార కాగితంను 64 సమాన చతురస్రాలుగా చేయబడింది. పెద్ద చతురస్రం చుట్టుకొలత కనుగొనుము. 64 చిన్న చతురస్రాల చుట్టుకొలతల మొత్తం కనుగొనండి. ఏమి గమనించితివి?
సాధన.
పెద్ద చతురస్ర భుజం = 8 సెం.మీ.
పెద్ద చతురస్ర చుట్టుకొలత = 4 × భుజం = 4 × 8 = 32 సెం.మీ.
పెద్ద చతురస్ర వైశాల్యం = 8 × 8 = 64 చ|| సెం.మీ.
ఒక చతురస్రాకార కాగితంను 64 సమాన చతురస్రాలుగా విభజించిన ఒక్కొక్క చిన్న చతురస్ర వైశాల్యం = \(\frac {64}{64}\) = 1 చ|| సెం.మీ.
భుజం × భుజం = 1 × 1 చ|| సెం.మీ.
ఒక్కొక్క చిన్న చతురస్ర భుజం = 1 సెం.మీ.
ఒక్కొక్క చిన్న చతురస్ర చుట్టుకొలత = 4 × భుజం = 4 × 1 = 4 సెం.మీ.
64 చిన్న చతురస్రాల మొత్తం చుట్టుకొలత = 64 × 4 = 256 సెం.మీ.
పై పరిశీలన నుండి మనం పెద్ద చతురస్ర చుట్టుకొలత, 64 చిన్న చతురస్రాల చుట్టుకొలతల మొత్తానికి సమానం కాదు అని గమనించగలము. అనగా ఒక జ్యామితీయ పటాన్ని అనేక చిన్న పటాలుగా విభజించినపుడు మనం క్రింది విషయాలు గమనించగలము.
(i) పెద్ద పటం యొక్క వైశాల్యము, విభజించిన అన్ని చిన్నపటాల వైశాల్యముల మొత్తానికి సమానము.
(ii) పెద్ద పటం యొక్క చుట్టుకొలత, అన్ని చిన్న పటాల చుట్టుకొలతల మొత్తానికి సమానం కాదు.