AP State Syllabus AP Board 6th Class Maths Solutions Chapter 11 Perimeter and Area Unit Exercise Textbook Questions and Answers.
AP State Syllabus 6th Class Maths Solutions 11th Lesson Perimeter and Area Unit Exercise
![]()
Question 1
Find the area of the square whose perimeter is 48 cm.
Solution:
Given perimeter of the square = 4 x s = 48 cm
Divide with 4 on both sides, \(\frac{4 \times \mathrm{s}}{4}=\frac{48}{4}\)
side (s) = 12 cm
Area of the square A = s x s = 12 x 12 = 144 sq. cm
Question 2.
If the length of a rectangle is 14cm and its perimeter is 3 times of its length. Find its area.
Solution:
Given the length of a rectangle l = 14 cm
Breadth of a rectangle b = ? cm
Perimeter of the rectangle = 2(l + b) = 3 times of length.
2(14 + b) = 3 x 14
Divide with 2 on both sides,
\(\frac{2(14+b)}{2}=\frac{3 \times 14}{2}\)
14 + b = 21
Subtract with 14 on both sides.
14 + b – 14 = 21 – 14
Breadth b = 7cm
Area of the rectangle A = l x b = 14 x 7 = 98 sq.cm
![]()
Question 3.
Find circumference of the circle whose diameter is 14 cm.
Solution:
Given the diameter of circle d = 14 cm
Circumference of the circle C = π.d
\(\frac{22}{7}\) x 14 =44 cm
Question 4.
14cm and 12cm are the length and breadth of a rectangle. If the breadth is increased by 6cm and length is decreased by 6cm, find the difference in areas.
Sol. Given length of the rectanglel = 14 cm
Breadth of the rectangle b = 12 cm
Area of the rectangle A1 = l x b
= 14 x 12 = 168 sq. cm
If length decreased by 6 cm, then length l = 14-6 = 8 cm
If breadth increased by 6cm, then breadth b = 12 + 6 = 18 cm
Then, the area of the rectangle A2 = l x b = 8 x 18 = 144 sq. cm
Difference of the areas = A1 – A2 = 168 – 144 = 24 sq. cm
Question 5.
Find the perimeter of the following figures. What did you observe?
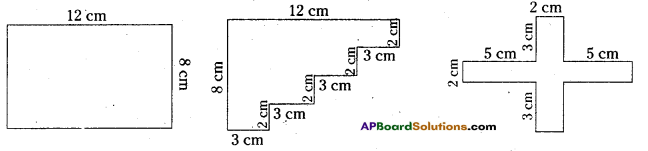
Solution:
i) Perimeter =12 cm + 8cm + 12cm + 8 cm = 40 cm
ii) Perimeter = 3cm + 2cm + 3cm + 2cm + 3cm + 2cm + 3cm + 2cm + 12cm + 8 cm = 40 cm
iii) Perimeter = 5cm + 3cm + 2cm + 3cm + 5cm + 2cm + 5cm + 3cm + 2cm + 3cm + 5cm + 2cm = 40 cm
By observing the perimeters of the above figures perimeters are same for the different shaped figures.
![]()
Question 6.
A square sheet of 8cm side was taken and made into 64 equal small squares. Find the perimeter of square sheet and also find the sum of the perimeters of all 64 small squares. What did you observe?
Solution:
Side of the square sheet s = 8cm
Perimeter of the square sheet = 4 x s = 4 x 8 = 32 cm
Side of the small square = 1cm
Perimeter of each small square = 4 x side = 4 x 1 = 4 cm
Perimeter of 64 small squares = 4 x 64 = 256 cm.
By observing sum of perimeters of all 64 small squares = 8 x perimeter of all squares.