AP State Syllabus AP Board 6th Class Maths Solutions Chapter 3 HCF and LCM Ex 3.6 Textbook Questions and Answers.
AP State Syllabus 6th Class Maths Solutions 3rd Lesson HCF and LCM Ex 3.6
Question 1.
Find the LCM of the following numbers by prime factorization method.
i) 12 and 15
ii) 15 and 25
iii) 14 and 21
Answer:
i) 12 and 15
To find the LCM of 12 and 15.
First find the factors of 12,15 and then find the common factors of 12 and 15.
12 = 2 x 2 x 3; 15 = 3 x 5
Prime factorization of 12 = 2 x 2 x 3
Prime factorization of 15 = 3 x 5
Common Factors of 12, 15 = 3
Extra factors of 12 and 15 = 2 x 2 x 5
∴ LCM of 12 and 15 = Common factor x extra factors
= 3 x 2 x 2 x 5 = 60
Hence the LCM of 12 and 15 is 60.
![]()
ii) 15 and 25
To find the LCM of 15 and 25.
First find the factors of 15, 25 and then find the common factors of 15 and 25.

Prime factorization of 15 = 3 x 5
Prime factorization of 25 = 5 x 5
Common factors of 15, 25 = 5
Extra factors of 15 and 25 = 3 x 5
∴ LCM of 15 and 25 = Common factor x extra factors
= 5 x 3 x 5 = 75
Hence the LCM of 15 and 25 is 75.
iii) 14 and 21
To find the LCM of 14 and 21.
First find the factors of 14, 21 and then find the common factors of 14 and 21.

Prime factorization of 14 = 2 x 7
Prime factorization of 21 = 3 x 7
Common factors of 14, 21 = 7
Extra factors of 14 and 21 = 2 x 3
LCM of 14 and 21 = Common factor x extra factors
= 7 x 2 x 3 = 42
Hence the LCM of 14 and 21 is 42.
![]()
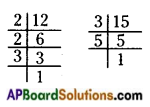
Question 2.
Find the LCM of the following numbers by division method.
i) 84, 112, 196
ii) 102, 119, 153
iii) 45, 99, 132, 165
Answer:
i) 84,112,196

∴ Thus, the LCM of 84, 112 and 196 is
2 x 2 x 2 x 2 x 3 x 7 x 7 = 2352
ii) 102, 119, 153

Thus, the LCM of 102,119 and 153 is
2 x 3 x 3 x 7 x 17 = 2142
iii) 45, 99, 132, 165

Thus, the LCM of 45, 99, 132 and 165 is
2 x 2 x 3 x 3 x 5 x 11 = 1980
![]()
Question 3.
Find the smallest number which when added to 5 is exactly divisible by 12,14 and 18.
Answer:
To find the number exactly divisible by 12, 14 and 18.
We have to find the LCM of 12, 14 and 18.

LCM of 12, 14 and 18 is 2 x 2 x 3 x 3 x 7 = 252
To get the smallest number we have to subtract 5 to the LCM of 12, 14 and 18 i.e., 252 – 5 = 247
Therefore, the smallest number which when added to 5 is exactly divisible by 12, 14 and 18 is 247.
Question 4.
Find the greatest 3 digit number which when divided by 75, 45 and 60 leaves
i) No remainder
ii) The remainder 4 in each case.
Answer:
i) To find the number exactly divisible (No remainder) by 75, 45 and 60.

We have to find the LCM of 75, 45 and 60.
LCM of 75, 45 and 60 is 900.
So, 990 is the greatest 3 – digit number which is exactly i divisible by the 75, 45 and 60.
ii) To get the remainder 4 when we divide the greatest 3 – digit number by 75, 45 and 60.
We have to add 4 to the greatest 3 – digit number, which is exactly divisible by 75, 45 and 60.
By adding 4 to 900 we get 904 (900 + 4)
Therefore, the greatest 3 – digit number divisible by 75, 45 and 60 by leaving remainder 4 is 994.
![]()
Question 5.
Two bells ring together. If the bells ring at every 3 minutes and 4 minutes respec-tively, at what interval of time, will they ring together again?
Answer:
Time interval for the first bell = 3 minutes
Time interval for the second bell = 4 minutes
Time interval for the bells together = LCM of 3 and 4
= 2 x 2 x 3 = 12 minutes

After 12 minutes the two bells again ring together.