AP State Syllabus AP Board 6th Class Maths Solutions Chapter 4 Integers Unit Exercise Textbook Questions and Answers.
AP State Syllabus 6th Class Maths Solutions 4th Lesson Integers Unit Exercise
Question 1.
Write the integers for the following situations.
i) A kite is flying at a height of 225 m in the sky. ( )
ii) A whale is at a depth of 1250 m in the ocean. ( )
iii) The temperature in Sahara desert is 12°C below freezing temperature. ( )
iv) Ravi withdrawn Rs. 3800 from ATM using his debit card. ( )
Answer:
i) 225 m
ii) – 1250 m
iii) – 12°C
iv) -3800
![]()
Question 2.
Justify the following statements with an example.
i) A positive integer is always greater than a negative integer.
ii) All positive integers are natural numbers.
iii) Zero is greater than a negative integer.
iv) There exist infinite integers in the number system.
v) All whole numbers are integers.
Answer:
i) A positive integer is always greater than a negative integer:
Consider
a) 3, -5 are two integers
3 > -5
b) – 10, 1 are two integers
1 > -10
∴ A positive integer is always greater than a negative integer.
ii) All positive integers are natural numbers:
Positive integers = 1, 2, 3, …..
Natural numbers = 1, 2, 3, …..
So, all positive integers are natural numbers.
iii) Zero is greater than a negative integer:
On a number line, for a given pair of numbers the number on R.H.S is always greater than the number on L.H.S.
All negative integers lie on the L.H.S. of zero, on a number line.
As such all negative numbers are less than zero or zero is greater than all negative integers.
iv) There exist infinite integers in the number system:
If we write integer on a number line, as the line extends on both sides endlessly so as the integers.
(Or)
For every integer there exists another integer which is 1 more than the given integer. Hence the integers are infinite.
v) All whole numbers are integers:
Whole numbers : 0, 1, 2, 3,……
Integers: ……, -3, -2, -1, 0, 1, 2, 3,…..
So, whole number are part of integers.
∴ All whole numbers are integers.
![]()
Question 3.
Represent
i) 3+4
ii) 8+(-3)
iii) -7-2
iv) 6-(5)
v)-5-(-4)
on number line.
Answer:
i) 3 + 4 = +7.

On the number line we first move 3 steps to the right of 0 to reach +3.
Then, we move 4 steps to the right of +3 and reach + 7.
ii) 8 + (-3) = +5.

On the number line we first move 8 steps to the right of 0 to reach +8.
Then, we move 3 steps to the left of +8 and reach +5.
iii) -7 -2 = -9

On the number line we first move 7 steps to the left of 0 to reach -7.
Then we move 2 steps to the left of -7 and reach -9.
iv) 6 – (5) = + 1

On the number line we first move 6 steps to the right of 0 to reach +6.
Then, we move 5 steps to the left of +6 and reach +1.
v) -5 – (-4) = -1
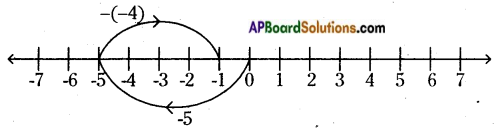
-5 – (-4) = -5 + 4 = -1 (∵ -(-a) = a)
On the number line, we first move 5 steps to the left of 0 to reach -5.
Then, we move 4 steps to the right of -5 and reach -1.
![]()
Question 4.
Write all the integers lying between the given numbers.
i) 7 and 12
ii) -5 and -1
iii) -3 and 3
iv) -6 and 0
Answer:
i) 7 and 12
Integers lying between 7 and 12 are 8, 9, 10, ll.
ii) -5 and -1
Integers lying between -5 and -1 are -2, -3 and -4.
iii) -3 and 3
Integers lying between -3 and 3 are -2, -1, 0, 1, 2.
iv) -6 and 0
Integers lying between -6 and 0 are -5, -4, -3, -2, -1.
Question 5.
Arrange the following integers in ascending order and descending order.
-1000, 10, -1, -100, 0, 1000, 1, -10
Answer:
Given numbers -1000, 10, -1, -100, 0, 1000, 1, -10
Ascending order: – 1000, -100, -10, -1, 0, 1, 10, 1000
Descending order: 1000, 10, 1, 0, -1, -10, -100, -1000
Question 6.
Write a real life situation for each of the following integers.
i) -200 m
ii) +42°C
iii) -4800(cr)
iv) -3.0 kg
Answer:
i) -200 m
In the Singareni coal mines workers will go 200 m below the ground level.
ii) +42°C
In summer average temperature of May month is 42°C.
iii) Rs. 4800 (crores)
Central Government sanctioned Rs. 4800(crores) for education in the Annual Budget.
iv) – 3.0 kg
In a Primary School the ground balance of rice = -3 kg
![]()
Question 7.
Find:
i) (-603) + (603)
ii) (-5281) +(1825)
iii) (-32) + (-2) + (-20) + (-6)
Answer:
i) (-603) + (603)
Sum of a number and its additive number is 0.
Additive inverse of – 603 is 603.
So, -603 + 603 = 0
ii) (-5281) + (1825)
= – 5281 + 1825 = – 3456

iii) (-32) + (-2) + (-20) + (-6)
= -32 – 2 – 20 – 6 = -60
Question 8.
Find:
i)(-2) – (+1)
ii) (-270) – (-270)
iii) (1000) – (-1000)
Answer:
i) -2 – (+1)
= -2 -1 = -3
ii) – 270 – (-270)
= -270 + 270 [∵ -(-a) = a]
= 0 [-a + a = 0]
iii) 1000 – (-1000)
= 1000 + 1000 [∵ -(-a) = a]
= 2000
![]()
Question 9.
In a quiz competition, where negative score for wrong answer is taken,Team A scored +10, -10, 0, -10, 10, -10 and Team B scored 10,10, -10,0,0,10 in 6 rounds successively .Which team wins the competition? How?
Answer:
Score of Team A = (+10), (-10), 0, (-10), 10, (-10)
Total score of Team A = (+10) + (-10) + (0) + (-10) + (10) + (-10)
= +10 – 10 + 0 – 10 + 10 – 10
= +20 – 30 = -10
Score of Team B = 10, 10, -10, 0, 0, 10
Total Score of Team B = (+10) + (+10) + (-10) + 0 + 0 + (+10)
= +10 + 10 – 10 + 10
= + 30 – 10
= + 20
-10 < + 20
Team A < Team B
So, Team B is the winner. Because, Team B got more score than Team A.
Question 10.
An apartment has 10 floors and two cellars for car parking under the basement. A lift is now, at the ground floor. Ravi goes 5 floors up and then 3 floors up, 2 floors down and then 6 floors down and come to lower cellar for taking his car. Count how many floors does Ravi travel all together? Represent the result on a vertical number line.
Answer:
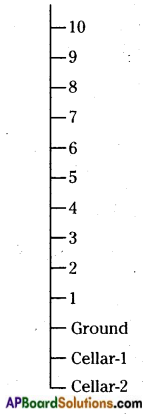
First move:
Ground to 5th floor up = 5
(Can reach 5th floor)
Second move:
5th floor to 3 floors up = 3
(Can reach 8)
Third move:
8th floor to 2 floors down = 2
(Can reach 6th floor)
Fourth move:
6th floor to 6 floors down = 6
(Can reach ground floor)
Final move:
Ground to lower cellar = 2
(Can reach cellar -2)
No. of floors Ravi travelled = 18