AP State Syllabus AP Board 8th Class Maths Solutions Chapter 12 Factorisation Ex 12.2 Textbook Questions and Answers.
AP State Syllabus 8th Class Maths Solutions 12th Lesson Factorisation Exercise 12.2
![]()
Question 1.
Factorise the following expression
i) a2 + 10a +25
ii) l2 – 16l + 64
iii) 36x2 + 96xy + 64y2
iv) 25x2 + 9y2 – 30xy
v) 25m2– 40mn + 1 6n2
vi) 81x2 – 198 xy + 12ly2
vii) (x+y)2 – 4xy
(Hint : first expand ( x + y)2 )
viii) l4 + 4l2m2 + 4m4
Solution:
i) a2 + 10a +25
= (a)2 + 2 × a × 5 + (5)2
It is in the form of a2 + 2ab + b2
a2 + 2ab + b2= (a + b)2
∴ a2 + 10a + 25 = (a + 5)2 = (a + 5) (a + 5)
![]()
ii) l2 – 16l + 64
l2 – 16l + 64
= (l)2 – 2 × l × 8 + (8)2
It is in the form of a2 – 2ab + b2
a2 – 2ab + b2 = (a – b)2
∴ l2 – 16l + 64 = (l – 8)2 = (l – 8) (l – 8)
iii) 36x2 + 96xy + 64y2
36x2 + 96xy + 64y2
= (6x)2 + 2 × 6x × 8y + (8y)2
It is in the form of a2 + 2ab + b2
a2 + 2ab + b2 = (a + b)2
∴ 36x2 + 96xy + 64y2
= (6x + 8y)2 = (6x + 8y) (6x + 8y)
![]()
iv) 25x2 + 9y2 – 30xy
25x2 + 9y2 – 30xy
= (5x)2 + (3y)2 – 2 × 5x × 3y
It is in the form of a2 + b2 – 2ab
a2 + b2 – 2ab = (a – b)2
∴ 25x2 + 9y2 – 30xy
= (5x – 3y)2 = (5x – 3y) (5x – 3y)
v) 25m2– 40mn + 1 6n2
25m2 – 40mn + 16n2
= (5m)2 – 2 × 5m × 4n + (4n)2
It is in the form of a2 – 2ab + b2
a2 – 2ab + b2 = (a – b)2
∴ 25m2 – 40mn + 16n2
= (5m – 4n)2
= (5m – 4n) (5m – 4n)
vi) 81x2 – 198 xy + 12ly2
81x2 – 198xy + 121y2
= (9x)2 – 2 × 9x × 11y + (11y)2
It is in the form of a2 – 2ab + b2
a2 – 2ab + b2 = (a – b)2
∴ 81x2 – 198xy + 121y2
= (9x – 11y)2 – (9x – 11y) (9x – 11y)
vii) (x+y)2 – 4xy
(Hint : first expand ( x + y)2 )
= (x + y)2 – 4xy
= x2 + y2 + 2xy – 4xy
= x2 + y2 – 2xy = (x – y)2 = (x – y)(x – y)
viii) l4 + 4l2m2 + 4m4
l4 + 4l2m2 + 4m4
= (l2)2 + 2 × l2 × 2m2 + (2m2)2
It is in the form of a2 + 2ab + b2
a2 + 2ab + b2 = (a – b)2
∴ l4 + 4l2m2 + 4m4
= (l2 + 2m2)2 = (l2 + 2m2) (l2 + 2m2)
![]()
Question 2.
Factorise the following
i) x2 – 36
ii) 49x2 – 25y2
iii) m2 – 121
iv) 81 – 64x2
v) x2y2 – 64
vi) 6x2 – 54
vii) x2 – 81
viii) 2x -32 x5
ix) 81x4 – 121x2
x) (p2 – 2pq + q2)-r2
xi) (x+y)2 – (x-y)2
Solution:
i) x2 – 36
x2 – 36
⇒ (x)2 – (6)2 is in the form of a2 – b2
a2 – b2 = (a + b) (a – b)
∴ x2 – 36 = (x + 6) (x – 6)
![]()
ii) 49x2 – 25y2
= (7x)2 – (5y)2
= (7x + 5y) (7x – 5y)
iii) m2 – 121
m2 -121
= (m)2 – (11)2
= (m + 11) (m – 11)
iv) 81 – 64x2
81 – 64x2
= (9)2 – (8x)2
= (9 + 8x) (9 – 8x)
v) x2y2 – 64
= (xy)2 – (8)2
= (xy + 8)(xy – 8)
vi) 6x2 – 54
6x2 – 54
= 6x2 – 6 x 9 ‘
= 6(x2 – 9)
= 6[(x)2 – (3)2]
= 6(x + 3) (x – 3)
![]()
vii) x2 – 81
x2 – 81
= x2 – 92
= (x + 9 )(x – 9)
viii) 2x – 32 x5
2x – 32 x5
= 2x – 2x x 16x4
= 2 x (1 – 16x4)
= 2x [12) – (4x2)2]
= 2x (1 + 4x2) (1 – 4x2)
= 2x (1 + 4x2) [(15 – (2x)2]
= 2x (1 + 4x2) (1 + 2x) (1 – 2x)
ix) 81x4 – 121x2
81x4 – 121x2
– x2 (812 – 121)
= x2[(9x)2 – (11)2]
= x2 (9x + 11) (9x -11)
x) (p2 – 2pq + q2)-r2
(p2 – 2pq + q2) – r2
= (p – q)2 – (r)2 [∵ p2 – 2pq + q2 = (p – q)2]
= (p – q + r) (p – q – r)
xi) (x + y)2 – (x – y)2
(x + y)2 – (x – y)2
It is in the form of a2 – b2
a = x + y, b = x- y
∴ a2 – b2 =(a + b)(a-b)
= (x + y + x – y) [x + y- (x – y)]
= 2x [x + y-x + y]
= 2x x 2y = 4xy
![]()
Question 3.
Factorise the expressions
(i) lx2 + mx
(ii) 7y2 + 35Z2
(iii) 3x4 + 6x3y + 9x2Z
(iv) x2 – ax – bx + ab
(v) 3ax – 6ay – 8by + 4bx
(vi) mn + m + n + 1
(vii) 6ab – b2 + 12ac – 2bc
(viii) p2q – pr2 – pq + r2
(ix) x (y + z) -5 (y + z)
(i) lx2 + mx
lx2 + mx
= l × x × x + m × x = x(lx + m)
(ii) 7y2 + 35z2
7y2+ 35z2
= 7 × y2 + 7 × 5 × z2
= 7(y2 + 5z2)
(iii) 3x4 + 6x3y + 9x2Z
3x4 + 6x3y + 9x2Z
= 3 × x2 × x2 + 3 × 2 × x × x2 × y + 3 × 3 × x2 × z
= 3x2 (x2 + 2xy + 3z)
![]()
(iv) x2 – ax – bx + ab
x2 – ax – bx + ab
= (x2 – ax) – (bx – ab)
= x(x – a) – b(x – a)
= (x – a) (x – b)
(v) 3ax – 6ay – 8by + 4bx
3ax – 6ay – 8by + 4bx
= (3ax – 6ay) + (4bx – 8by)
= 3a (x – 2y) + 4b (x – 2y)
= (x – 2y) (3a + 4b)
(vi) mn + m + n + 1
mn + m + n + 1
= (mn + m) + (n + 1)
= m (n + 1) + (n + 1)
= (n + 1) (m + 1)
(vii) 6ab – b2 + 12ac – 2bc
6ab – b2 + 12ac – 2bc
= (6ab – b2) + (12ac – 2bc)
= (6 × a× b – b × b) + (6 × 2 × a × c – 2 × b × c)
= b [6a – b] + 2c [6a – b]
= (6a – b) (b + 2c)
(viii) p2q – pr2 – pq + r2
p2q – pr2 – pq + r2
= (p2q – pr2) – (pq – r2)
= (p × p × q – p × r × r) – (pq – r2)
= P(pq – r2) – (pq – r2) × 1
= (pq – r2)(p – 1)
(ix) x (y + z) -5 (y + z)
= x(y + z) – 5(y + z)
= (y + z) (x – 5)
![]()
Question 4.
Factorise the following
(i) x4 – y4
(ii) a4 – (b + c)4
(iii) l2 – (m – n)2
(iv) 49x2 – \(\frac{16}{25}\)
(v) x4 – 2x2y2 + y4
(vi) 4 (a + b)2 – 9 (a – b)2
Solution:
= (x2)2 – (y2)2 is in the form of a2 – b2
a2 – b2 = (a + b) (a – b)
x4 – y4 = (x2 + y2)(x2 – y2)
= (x2 + y2)(x + y)(x – y)
(ii) a4 – (b + c)4
a4 – (b + c)4
= (a2)2 – [(b + c)2]2
= [a2 + (b + c)2] [a2 – (b + c)2] ,
= [a2 + (b + c)2] (a + b + c) [a – (b + c)]
= [a2 + (b + c)2] (a + b + c) (a – b – c)
(iii) l2 – (m – n)2
l2 – (m – n)2
= (l)2 – (m – n)2
= [l + m – n] [l – (m – n)]
= [l + m -n] [l – m + n]
![]()
(iv) 49x2 – \(\frac{16}{25}\)
= (7x)2 – (\(\frac{4}{5}\))2
= (7x+ (\(\frac{4}{5}\)) (7x – (\(\frac{4}{5}\))
(v) x4 – 2x2 y2 + y4
= (x2 )2 – 2x2 y2 + (y2 )2
It is in the form of a2 – 2ab + b2
a2 – 2ab + b2 = (a – b)2
∴ x4 – 2x2 y2 + y4 = (x2 – y2 )2
= [(x)2 – (y)2 ]2
= [(x + y) (x – y)]2
= (x + y)2 (x – y)2
[∵ (ab)m = a m . bn ]
(vi) 4 (a + b)2 – 9 (a – b)2
4 (a + b)2 – 9 (a – b)2
= [2(a + b)]2 – [3(a – b)]2
= [2(a + b) + 3(a- b)] [2(a + b)-3(a- b)]
= (2a + 2b + 3a – 3b) (2a + 2b – 3a + 3b)
= (5a – b) (5b – a)
![]()
Question 5.
Factorise the following expressions
(i) a2+ 10a + 24
(ii) x2 +9x + 18
(iii) p2 – 10q + 21
(iv) x2 – 4x – 32
Solution:
(i) a2+ 10a + 24
a2 + 10a + 24 .
= a2 + 6a + 4a + 24
= a x a + 6a + 4a + 6 × 4
= a(a + 6) + 4(a + 6)
= (a + 6) (a + 4) (or)
a2 + 10a + 24
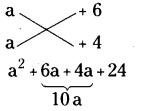
∴ a2 + 10a + 24 = (a + 6) (a + 4)
(ii) x2 + 9x + 18
x2 + 9x + 18
= (x + 3) (x + 6)
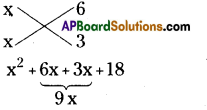
∴ x2 + 9x + 18 = (x + 3) (x + 6)
(iii) p2 – 10q + 21
p2 – 10p + 21
= (P – 7) (p – 3)
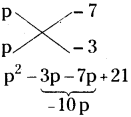
∴ p2 – 10p + 21 = (p – 7)(p – 3)
![]()
(iv) x2 – 4x – 32
x2 – 4x – 32
= (x – 8) (x + 4)
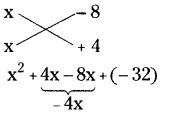
∴ x2 – 4x – 32 = (x – 8) (x + 4)
Question 6.
The lengths of the sides of a triangle are integrals, and its area is also integer. One side is 21 and the perimeter is 48. Find the shortest side.
Solution:
Perimeter of a triangle
= AB + BC + CA = 48
⇒ c + a + b = 48
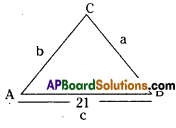
The solutions of Harmeet, Rosy are wrong.

∴ Srikar had done it correctly.
⇒ 21 + a + b = 48
⇒ a + b = 48 – 21 = 27
∴ The lengths of a, b should be 10, 17
∴ a + b > c [the sum of any two sides of a triangle is greater than the 3rd side]
∴ 10 + 17 > 2
27 > 21 (T).
∴ The length of the shortest side is 10 cm.
![]()
Question 7.
Find the values of ‘m’ for which x2 + 3xy + x + my – in has two linear factors in x and y, with integer coefficients.
Solution:
Given equation is x2 + 3xy + x + my – m ……….(1)
Let the two linear equations in x and y be (x + 3y + a) and (x + 0y + b).
Then (x + 3y + a) (x + 0y + b)
= x2 + 0xy + bx + 3xy + 0y2 + 3by + ax + 0y + ab
= x2 + bx + ax + 3xy + 3by + ab ………….. (2)
Comparing equation (2) with (1),
x2 + 3xy + x + my – m
= x2 + (a + b)x + 3xy + 3by + ab
Equating the like terms on both sides,
ab = – m ………….. (3)
(a + b)x = x ⇒ a + b = 1 ……………. (4)
3by = my ⇒ 3b = m ⇒ b = \(\frac{\mathrm{m}}{3}\)
Substitute ‘b’ value in equation (4),
a = \(1-\frac{m}{3}=\frac{3-m}{3}\)
ab = -m
[ ∵ from (3)]
put a & b value then ,
\(\left(\frac{3-m}{3}\right)\left(\frac{m}{3}\right)\) = -m
\(\frac{3 \mathrm{~m}-\mathrm{m}^{2}}{9}\)= -m
⇒ 3m – m2 = – 9m
⇒ m2 – 12m = 0
⇒ m(m – 12) = 0
⇒ m = 0 (or) m = 12
lf m = 12
∴ b = \(\frac{12}{3}\) = 4&a = \(\frac{3-\mathrm{m}}{3}=\frac{3-12}{3}\)
= \(\frac{-9}{3}\) = -3
∴ Linear factors are (x + 3y – 3), (x + 4) If m = 0
b = \(\frac{0}{3}\) = 0 & a = \(\frac{3-0}{3}=\frac{3}{3}\) = 1
∴ Linear factors are (x + 3y + 1), x.