AP State Syllabus AP Board 8th Class Maths Solutions Chapter 14 Surface Areas and Volumes Ex 14.1 Textbook Questions and Answers.
AP State Syllabus 8th Class Maths Solutions 14th Lesson Surface Areas and Volumes Exercise 14.1
![]()
Question 1.
There are two cuboidal boxes as shown in the given figure. Which box requires the less amount of material to make?
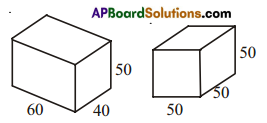
Solution:
Volume of a cuboid V1 = lbh
= 60 × 40 × 50
V1 = 1,20,000 cubic units.
Volume of a cube V2 = (a)3
= (50)3 = 50 × 50 × 50
V2 = 1,25,000 cubic units.
∴ The cuboidal box requires less amount of material.
∴ V1 < V2
![]()
Question 2.
Find the side of a cube whose surface area is 600 cm2
Solution:
Total surface area of a cube = 6a2
⇒ 6a2 = 600
⇒ a2 = \([latex]\frac { 600 }{ 6 }\)[/latex] = 100
⇒ a2 = 100
⇒ a = √100 = 10
∴ The side of a cube (a) = 10 cm.
![]()
Question 3.
Prameela painted the outer surface of a cabinet of measures 1m × 2m × 1 .5m. Find the surface area she cover if she painted all except the bottom of the cabinet?
Solution:
The area of outer surface of a cabinet except the bottom of the cabinet will be equal to its lateral surface area.
I = lm,b = 2m, h = 1.5m.
A = 2h(l + b)
= 2 × 1.5(1 + 2)
= 3 × 3 = 9 m2.
![]()
Question 4.
Find the cost of painting a cuboid of dimensions 20cm × 15 cm × 12 cm at the rate of 5 paisa per square centimeter.
Solution:
l = 20cm, b = 15cm, h = 12cm.
∴ Total surface area of a cuboid
A = 2 (lb + bh + lh)
=2(20 × 15 + 15 × 12 + 20 × 12)
= 2 (300 + 180 + 240)
= 2 × 720
= 1440 sq.cm.
The cost of painting a cuboid at the rate of 5 paisa per sq. cm for 1440 sq.cm.
= 1440 × 5 paisa
= 7200 paise
= ₹ \(\frac { 7200 }{ 100 }\)
= ₹ 72