AP State Syllabus AP Board 8th Class Maths Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 Textbook Questions and Answers.
AP State Syllabus 8th Class Maths Solutions 14th Lesson Surface Areas and Volumes Exercise 14.2
![]()
Question 1.
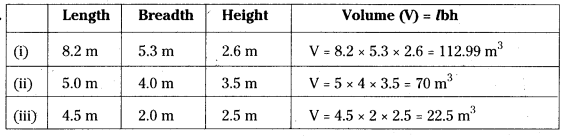
Find the volume of the cuboid whose dimensions are given below.
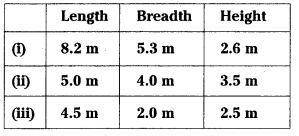
Solution:
Question 2.
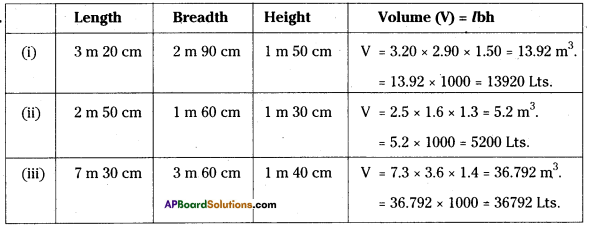
Find the capacity of the tanks with the following internal dimensions. Express the capacity in cubic meters and litres for each tank.
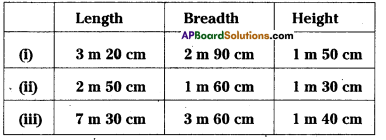
Solution:
![]()
Question 3.
What will happen to the volume of a cube if the length of its edge is reduced to half? Is the volume get reduced? If yes, how much?
Solution:
Volume of a cube of side (s) is V1 = a3
If the length of the side is reduced by half then
s = \(\frac{\mathrm{a}}{2}\)
∴ Volume of cube (V2 ) = s3

∴ V2 = \(\frac { 1 }{ 8 }\) × V1
∴ V1 = 8V2
![]()
Question 4.
Find the volume of each of the cube whose sides are.
(i) 6.4 cm
(ii) 1.3 m
(iii) 1.6 m.
Solution:
Volume of a cube(V) = a3
i) a = 6.4 cm
ii) a = 1.3 m
iii) a = 1.6 m
V = (6.4)3
Volume of a cube (V) = a3
= 6.4 × 6.4 × 6.4
= 262.144 cm3
V = (1.3)3
= 1.3 × 1.3 × 1.3
= 2.197 m3
V = (1.6)3
= 1.6 × 1.6 × 1.6
= 4.096 m3
![]()
Question 5.
How many bricks will be required to build a wall of 8 m long, 6m height and 22.5 cm thici if each brick measures 25 cm by 11.25 cm by 6 cm?
Solution:
The volume of a wall of measures
8 m × 22.5 cm × 6 m
(V1) = l1b1h1
= 8 m × 22.5 cm × 6 m
= 800 cm × 22.5 cm × 600 cm
The volume of a brick each measures
25 cm × 11.25 cm × 6 cm
(V2) = l2b2h2
= 25 × 11.25 × 6 cm3
∴ The no.of bricks will be required
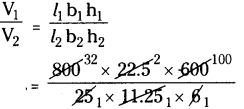
= 32 × 2 × 100 = 6400
Question 6.
A cuboid is 25 cm long, 15 cm broad, and 8 cm high . How much of its volume will differ from that of a cube with the edge of 16 cm’?
Solution:
Volume of a cuboid (V1) of measures
= 25 cm, b = 15 cm, h = 8 cm.
V1 = 25 × 15 × 8 = 3000 cm3
Volume of a cube of measure side (s) = 16 cm is
V2 = (s)3 = (16)3 = 16 × 16 × 16
= 4096 cm3
The difference between their volumes
= V2 – V1
= 4096 – 3000
= 1096 cm3
![]()
Question 7.
A closed box is made up of wood which is 1cm thick .The outer dimensions of the box is 5 cm × 4 cm × 7 cm. Find the volume of the wood used.
Solution:
The volume of a box formed with outer measures 5 cm × 4 cm × 7 cm
V1 = l × b × h
= 5 × 4 × 7
∴ V1 = 140 cm3
Inner measures
= l – 2w, b – 2w, h – 2w
= (5 – 2 × 1), (4 – 2 × 1), (7 – 2 × 1)
= (5 – 2), (4 – 2), (7 – 2)
= 3 cm, 2 cm, 5 cm
∴ Volume of a box formed with inner measures
V2 = (l – 2w)(b – 2w)(h – 2w)
= 3 × 2 × 5 = 30 cm3
∴ The volume of wood used = V1 – V2
= 140 – 30 = 110 cm3
![]()
Question 8.
How many cubes of edge 4cm, each can be cut out from cuboid whose length, breadth and height are 20 cm, 18 cm and 16 cm respectively
Solution:
The volume of a cuboid formed with the measures 20 cm × 18 cm × 16 cm
(V1) = l1b1h1 = 20 × 18 × 16
Volume of a cube (V2) = s3
s = 4 cm (given)
∴ V2 = (s)3 = (4)3= 4 × 4 × 4 cm3
∴ No.of cubes are required
= \(\frac{V_{1}}{V_{2}}=\frac{20 \times 18 \times 16}{4 \times 4 \times 4}\)
= 90
Question 9.
How many cuboids of size 4 cm × 3 cm × 2 cm can be made from a cuboid of size 12 cm x 9cm x 6cm?
Solution:
Volume of a cuboid of measures 12 cm × 9 cm × 6 cm
V1 = l × b × h = 12 × 9 × 6
Volume of the smaller cuboid of measures 4 cm × 3 cm × 2 cm
V2 = l2b2h2 = 4 × 3 × 2
∴ No.of cuboids are made
= \(\frac{V_{1}}{V_{i}}=\frac{12 \times 9 \times 6}{4 \times 3 \times 2}\) = 27
Question 10.
A vessel in the shape of a cuboid is 30 cm long and 25 cm wide. What should be its height to hold 4.5 litres of water ?
Solution:
Length of a cuboidal vessel (l) = 30 cm
breadth (b) = 25 cm
height (h) = ?
The volume of water m a cuboidal vessel = 4.5 Lts.
= 4.5 × 1000 cm3
= 4500 cm3
∴ l × b ×h = 4500
⇒ 30 × 25 × h = 4500
⇒ h = \(\frac{4500}{30 \times 25}\)
∴ h = 6 cm
∴ Height of the vessel (h) = 6 cm