AP Board 8th Class Maths Solutions Chapter 14 ఉపరితల వైశాల్యము మరియు ఘనపరిమాణం (ఘనము-దీర్ఘఘనము) InText Questions

AP SCERT 8th Class Maths Textbook Solutions Chapter 14 ఉపరితల వైశాల్యము మరియు ఘనపరిమాణం (ఘనము-దీర్ఘఘనము) InText Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 14th Lesson ఉపరితల వైశాల్యము మరియు ఘనపరిమాణం InText Questions

ఇవి చేయండి

1. ఈ క్రింది దీర్ఘఘనముల యొక్క సంపూర్ణతల వైశాల్యమును కనుగొనుము. (పేజీ నెం. 298)

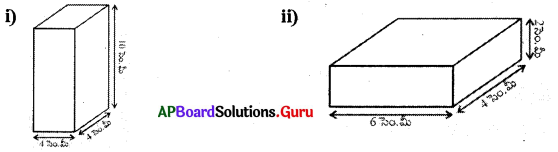
సాధన.
(i) l = 4 సెం.మీ., b = 4 సెం.మీ., h = 10 సెం.మీ.
దీర్ఘఘనం యొక్క సంపూర్ణతల వైశాల్యం = 2 (lb + bh + lh)
= 2(4 × 4 + 4 × 10 + 4 × 10)
= 2(16 + 40 + 40)
= 2 × 96 = 192 చ.సెం.మీ.
(ii) l = 6 సెం.మీ., b = 4 సెం.మీ., h = 2 సెం.మీ.
దీర్ఘ ఘనం యొక్క సంపూర్ణతల వైశాల్యం = 2 (lb + bh + lh)
= 2 (6 × 4 + 4 × 2+ 6 × 2)
= 2 (24 + 8 + 12)
= 2 × 44 = 88 చ.సెం.మీ.

2. 6 సెం.మీ., 4 సెం.మీ. మరియు 5 సెం.మీ. కొలతలుగా గల దీర్ఘఘనము యొక్క ఘనపరిమాణమును కనుక్కోండి. (పేజీ నెం. 305)

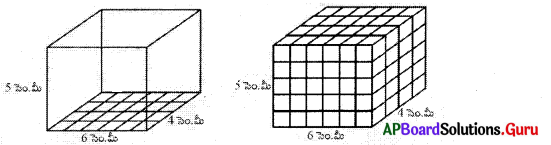
ఒక ఘనపు భుజము సెం.మీ. గా గల ప్రమాణ ఘనములను దీర్ఘఘనము పొడవు వెంబడి పేర్చుము. దీని కొరకు మనకు ఎన్ని ఘనములు అవసరము ? 6 ప్రమాణ ఘనములు అవసరము. వెడల్పు వెంబడి ఎన్ని ప్రమాణు ఘనములు పేర్చవచ్చు ? 4 ప్రమాణ ఘనములు దీనికి గల కారణము దీర్ఘ ఘనము యొక్క వెడల్పు 4 సెం.మీ. అనగా ఒక పారలో 6 × 4 ప్రమాణ ఘనములు ఉంటాయి.

దీర్ఘ ఘనములో ప్రమాణ ఘనములు అమర్చే పొరలు ఎన్ని ? 5 పొరలు అనగా దీర్ఘఘనము యొక్క ఎత్తు 5 సెం.మీ. ప్రతి పౌర 6 × 4 ఘనములు కలవు. కావున 5 పొరలలో 6 × 4 × 5 ప్రమాణ సమఘనాల దిమ్మలు ఉంటాయి. అనగా l × b × hకు సమానం.
పై చర్చ దీర్ఘఘనము యొక్క ఘనపరిమాణమునకు సూత్రము నిచ్చును.
దీర్ఘఘన ఘనపరిమాణము = పొడవు × వెడల్పు × ఎత్తు
సాధన.
6 సెం.మీ., 4 సెం.మీ. మరియు 5 సెం.మీ. కొలతలు గల దీర్ఘ ఘనం యొక్క ఘనపరిమాణం
V= lbh ⇒ V = 6 × 4 × 5 ⇒ V = 120 సెం.మీ³

3. 64 ప్రమాణ ఘనములను ఉపయోగించి మీరు ఏర్పరచగల దీర్ఘఘనములు ఎన్ని ? ప్రతీ అమరిక యొక్క సంపూర్ణతల వైశాల్యము కనుక్కోండి. సమాన ఘనపరిమాణము కలిగిన ఘనముల యొక్క ప్రక్కతల వైశాల్యములు సమానమేనా ? (పేజీ నెం. 306)
సాధన.
64 ప్రమాణ ఘనములను ఉపయోగించి మీరు ఏర్పరచగల దీర్ఘఘనాల సంఖ్య
64 = 1 × 64 ……….. (1)
= 2 × 32 ………………… (2)
= 4 × 16 ………………….. (3)
ఈ విధంగా 3 విధాలుగా దీర్ఘఘనాలను ఏర్పర్చవచ్చు.
1. l = 64 సెం.మీ. , b = 1 సెం.మీ., h = 1 సెం.మీ.
దీర్ఘఘనం యొక్క సంపూర్ణతల వైశాల్యము = 2 (lb+ bh + lh)
= 2(64 × 1 + 1 × 1 + 1 × 64)
= 2 (64 + 1 + 64) = 2 × 129 = 258 చ.యూ.

2. l = 32 సెం.మీ., b = 2 సెం.మీ., h = 1 సెం.మీ.
A = 2 (lb + bh + lh)
= 2 (32 × 2 + 2 × 1 + 32 × 1)
= 2 (64 + 2 + 32)
= 2 × 98 = 196 చ.యూ.

3. l = 16 సెం.మీ., b = 4 సెం.మీ., h = 1 సెం.మీ.
A = 2(lb+ bh + lh)
= 2(16 × 4 + 4 × 1 + 16 × 1)
= 2 (64 + 4 + 16)
= 2 × 84 = 168 చ.యూ.

ప్రయత్నించండి

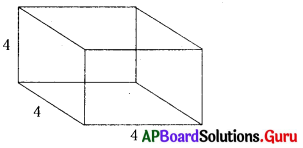
1. (i) సమ ఘనము ‘A’ యొక్క సంపూర్ణతల వైశాల్యం మరియు ‘B’ యొక్క ప్రక్కతల వైశాల్యము కనుగొనండి. (పేజీ నెం. 300)

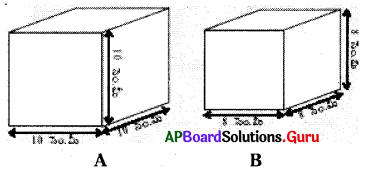
సాధన.
a = 10 సెం.మీ.
పటం A యొక్క సంపూర్ణతల వైశాల్యము = 6a²
= 6 × (10)²
= 6 × 100 = 600 చ.సెం.మీ.
పటం B యొక్క ప్రక్కతల వైశాల్యము = 4a²
= 4 × (8)² [∵ a = 8 సెం.మీ. ]
= 4 × 64 = 256 చ.సెం.మీ.

(ii) ‘b’ భుజముగా గల రెండు సమఘనములు పటములో చూపిన విధముగా జతచేయబడి దీర్ఘఘనమును ఏర్పరిస్తే, ఆ దీర్ఘఘనము యొక్క సంపూర్ణతల వైశాల్యము ఎంత ?

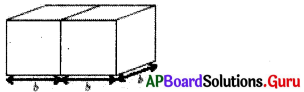
సాధన.
ప్రక్క దీర్ఘఘనం యొక్క సంపూర్ణతల వైశాల్యం = 2 (lb + bh + lh)

= 2(2b × b + b × b + 2b × b)
= 2(2b² + b² + 2b²)
= 2(5b²) = 10b² చ.యూ.

(iii) సమాన భుజము పొడవు గల 12 సమఘనములు ఏ విధముగా జతచేయడము వలన అత్యల్ప సంపూర్ణతల వైశాల్యము కలిగిన దీర్ఘ ఘనము ఏర్పడుతుందో వివరింపుము.

సాధన.
12 సమఘనాలను ఒకదాని ప్రక్క ఒకటి లేదా ఒకదానిపై ఒకటి అమర్చుట ద్వారా అత్యల్ప సంపూర్ణతల వైశాల్యం సంభవించదు.

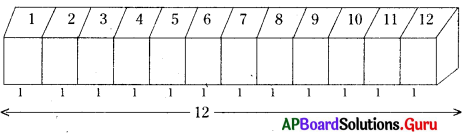
∴ A = 2(lb + bh + lh)
= 2(12 × 1 + 1 × 1 + 12 × 1)
= 2(12 + 1 + 12)
= 2 × 25 = 50 చ.యూ
కానీ, 3 సమఘనాలపై నాలుగు వరుసలుగా అమర్చుట ద్వారా అత్యల్ప సంపూర్ణతల వైశాల్యం పొందవచ్చు.
∴ A = 2(lb+ bh + lh)
= 2(3 × 1 + 1 × 4 + 3 × 4) (∵ l = 3; b = 1; h = 4)
= 2(3 + 4 + 12) = 2 × 19 = 38 చ.యూ.

(iv) 4 × 4 × 4 కొలతలు గల ఒక సమఘనము రంగు వేయబడినది. ఆ ఘనము 64 సమఘనములుగా విభజింప బడినది. అయితే
(a) ఒక ముఖము మాత్రమే రంగు వేయబడినది. ఘనములు ఎన్ని ?
(b) రెండు ముఖములు రంగు వేయబడిన ఘనములు ఎన్ని ?
(c) మూడు ముఖములు రంగు వేయబడిన ఘనములు ఎన్ని ?
(d) ఏ ముఖము కూడ రంగు వేయబడని ఘనములు ఎన్ని ?
సాధన.
4 × 4 × 4 సమఘనం 64 సమఘనాలుగా విభజింపబడిన ఒక్కొక్క
సమఘనం యొక్క భుజం పొడవు = 1 యూ.

[∵ \(\frac{4 \times 4 \times 4}{64}\) = 1]
(a) ఒక ముఖము మాత్రమే రంగు వేయబడిన (a = 4) సమఘనాల సంఖ్య = 6(a – 2)² = 6(4 – 2)² = 6 × 4 = 24
(b) రెండు ముఖాలు రంగు వేయబడిన సమఘనాల సంఖ్య = 12(a – 2) = 12(4 – 2) = 24
(c) మూడు ముఖాలు రంగు వేయబడిన సమఘనాల సంఖ్య 4 × a = 4 × 2 = 8
(d) ఏ ముఖం కూడా రంగు వేయబడని సమఘనాల సంఖ్య = (a – 2)³ = (4 – 2)³ = (2)³ = 8

ఆలోచించి, చర్చించి వ్రాయండి

1. దీర్ఘఘనం సంపూర్ణతల వైశాల్యము = ప్రకృతల వైశాల్యము + 2 × భూవైశాల్యము అని మీరు చెప్పగలరా ? (పేజీ నెం. 299)

సాధన.
దీర్ఘఘనం సంపూర్ణతల వైశాల్యం = ప్రక్కతల వైశాల్యం + 2 × భూవైశాల్యం
= 2h(l + b) + 2 × lb
= 2lh +2bh +2lb
= 2(lb + bh + lh)
∴ దీర్ఘఘనం సంపూర్ణతల వైశాల్యం = ప్రక్కతల వైశాల్యం + 2 × భూవైశాల్యం అని చెప్పగలం.

2. పటము (i)లో చూపిన దీర్ఘఘనము భంగిమను పటము (ii)లో లాగ మార్చిన వాటి ప్రక్కతల వైశాల్యాలు సమానంగా ఉంటాయా ?
సాధన.
దీర్ఘఘనం యొక్క భంగిమను ఏ విధంగా మార్చినా దాని ప్రక్కతల వైశాల్యములు సమానంగా ఉండవు.

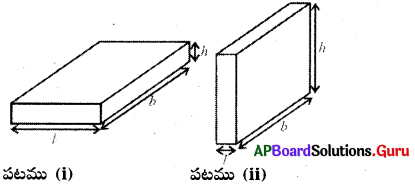
3. పొడవు (i), వెడల్పు (b), ఎత్తు (h) ల కొలతలు సమానముగా గల దీర్ఘఘనపు పటమును గీచి దాని ప్రక్కతల వైశాల్యము మరియు సంపూర్ణతల వైశాల్యములకు సూత్రము రాబట్టుము.
సాధన.
దీర్ఘఘనం యొక్క ప్రక్కతల వైశాల్యం

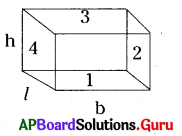
= 4 × ప్రక్కతల వైశాల్యము
= 2 (l × h) + 2 × (b × h) (1 + 2 + 3 + 4 తలాలు)
= 2h (l + b) చ.యూ. (1 = 3, 4 = 2)
దీర్ఘ ఘనం యొక్క సంపూర్ణతల వైశాల్యం = 4 × ప్రక్కతల వైశాల్యం + పైన, క్రింది తలాల వైశాల్యం
= 2h (l + b) + 2(lb)
= 2lh + 2bh + 2lb
= 2(lb + bh + lh) చ.యూ.