AP State Syllabus AP Board 8th Class Maths Solutions Chapter 15 Playing with Numbers Ex 15.6 Textbook Questions and Answers.
AP State Syllabus 8th Class Maths Solutions 15th Lesson Playing with Numbers Exercise 15.6
![]()
Question 1.
Find the sum of integers which are divisible by 5 from 1 to 100.
Solution:
Numbers which are divisible by 5 from 1 to 100 are 5, 10, 15, …………………95, 100.
∴ Sum of the above numbers = 5+10 + ……………..+ 95 + 100
= 5[1 + 2 + ………………….+ 20]
= 5 [ \(\frac{20 \times(20+1)}{2}\) ]
= \(\frac{5 \times 20 \times 21}{2}\) [∵ Sum of ‘n’ natural numbers = \(\frac{n(n+1)}{2}\) & n = 20 ]
= 1050
![]()
Question 2.
Find the sum of integers which are divisible by 2 from 11 to 50.
Solution:
. Numbers which are divisible by 2 from 11 to 50 are 12, 14,48, 50.
Sum of the numbers = 12 + 14 + ……….. + 48 + 50 ‘
= (2 + 4 + ……….. + 50) – (2 + 4 + ……….. + 10)
= 2(1 + 2 +……….. + 25) – 2 (1 + 2 + ……….. + 5)
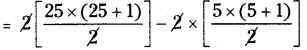
= 25 × 26 – 5 × 6
= 650 – 30
= 620
Question 3.
Find the sum of integers which are divisible by 2 and 3 from 1 to 50.
Solution:
Numbers which are divisible by 2 and 3 i.-e., which are divisible by 6 from 1 to 50 are 6,12 …………….48.
Sum of the numbers = 6 + 12 + ……..+ 48
= 6(1 + 2 +……… + 8)
= 6 \(\left[\frac{8(8+1)}{2}\right]\)
= 3 × 8 × 9 = 216
![]()
Question 4.
(n3 – n) is divisible by 3. Explain the reason.
Solution:
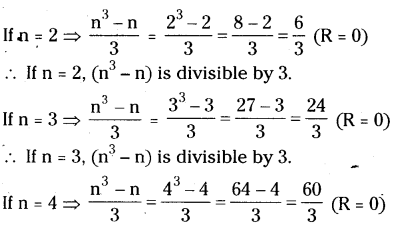
∴ If n = 4, (n3 – n) is divisible by 3.
∴ (n3 – n) is divisible by all the values of n.
Method 2:
n3 – n = n(n2 – 1)
= n(n + 1)(n – 1)
∴ (n3 – n) is divisible by ‘3’ for all the values of n.
[∵ (n – 1), n, (n + 1) are three consecutive odd numbers]
Question 5.
Sum of ‘n’ odd number of consecutive numbers is divisible by ‘n’. Explain the reason.
Solution:
Sum of n’ consecutive odd numbers = n2
Since n is a factor of n2, It Is divisible by ‘n’.
Question 6.
Is 111 + 211 + 311 + 411 divisible by 5? Explain.
Solution:
Sum of units digit of number 111 + 211 + 311 + 411
= 1 + 8 + 7 + 4
= 20 → \(\frac{20}{5}\)(R = 0)
∴ 111 + 211 + 311 + 411 is divisible by 5.
![]()
Question 7.
![]()
Find the number of rectangles of the given figure?
Solution:
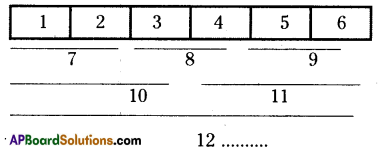
∴ No.of rectangles in the given figure = 1 + 2 + 3 + 4 + 5 + 6 = 21
Question 8.
Rahul’s father wants to deposit sorne amount of money every year on the day of Rahul’s birthday. On his 1st birth day Rs.100, on his 2nd birth day Rs.300, on his 3 birth day Rs.600, on his 4th birthday Rs. 1000 and so on. What is the amount deposited by his father on Rahul’s 15th birthday.
Solution:

Rahul’s father deposits on every year 200, 300, 400 more than before year.
Then he deposits ₹ 10,500 on 14th birthday.
∴ The amount deposits on 15th birthday
= 10,500 + 1,500
= ₹ 12,000/-
![]()
Question 9.
Find the sum of integers from 1 to 100 which are divisible by 2 or 5.
Solution:
Sum of the numbers which are divisible by 2 from 1 to 100
= 2 + 4 + ……….. + 100
= 2(1 + 2 + ………… +50)
= 2 × \(\frac{50 \times(50+1)}{2} \)
= 50 × 51 = 2550
Sum of the numbers which are dMsible by 5froin I to 100
= 5 + 10 + ……….. + 100
= 5(1 + 2 +……….. +20)
= 5 × \(\frac{20 \times(20+1)}{2}\)
=5 × 10 × 21
=1050
Sum of the numbers which are.divisible by both 2 and 5 = 2550 + 1050 =3600
∴ Sum ol the numbers which are divisible by 2 or 5 from 1 to 100
= 10 + 20 + ………..+ 100 ( L.C.M of 2, 5 is 10)
=10(1 + 2 + ………..+ 10)
= 10 × \(\frac{10 \times(10+1)}{2}\)
= 5 × 10 × 11 .
= 550
∴ The sum of required numbers 3600—550 3050
![]()
Question 10.
Find the sum of integers from 11 to 1000 which are divisible by 3.
Solution:
Sum ol the numbers which are divisible by 3 from lito 1000
= 12 + 15+ ……….. +099
= 3(4 + 5 + ……….. +333)
= 3(1 + 2 + ……….. + 333) – 3(1 + 2+3)
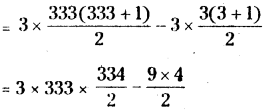
= 999 × 167 – 9 × 2
= 166833 – 18
= 166815