AP State Syllabus AP Board 8th Class Maths Solutions Chapter 2 Linear Equations in One Variable Ex 2.4 Textbook Questions and Answers.
AP State Syllabus 8th Class Maths Solutions 2nd Lesson Linear Equations in One Variable Exercise 2.4
![]()
Question 1.
Find the value of ’x’ so that l || m
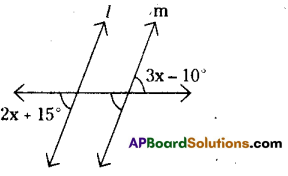
Solution:
Given l|| m. Then 3x – 10° = 2x + 15°
[Vertically opposite angles and corresponding angles are equal.]
⇒ 3x – 10 = 2x + 15
⇒ 3x – 2x = 15 + 10
∴ x = 25°
![]()
Question 2.
Eight times of a number reduced by 10 is equal to the sum of six times the number and 4. Find the number.
Solution:
Let the number be ‘x’ say.
8 times of a number = 8 × x = 8x
¡f10 is reduced from 8x then 8x – O
6 times of a number = 6 × x = 6x
If 4 is added to 6x then 6x + 4
According to the sum,
8x – 10 = 6x + 4
⇒ 8x – 6x = 4 + 10
⇒ 2x = 14
⇒ x = 7
∴ The required number = 7
![]()
Question 3.
A number consists of two digits whose sum is 9. If 27 is subtracted from the number its digits are reversed. Find the number.
Solution:
Let a digit of two digit number be x.
The sum of two digits = 9
∴ Another digit = 9 – x
The number = 10 (9 – x) + x
= 90 – 10x + x
= 90 – 9x
If 27 is subtraçted from the number its digits are reversed.
∴ (90 – 9x) – 27 = 10x + (9 – x)
63 – 9x = 9x + 9
9x + 9x = 63 – 9
18x = 54
∴ x = \(\frac { 54 }{ 18 }\) = 3
∴ Units digit = 3
Tens digit = 9 – 3 = 6
∴ The number = 63
![]()
Question 4.
A number is divided into two parts such that one part is 10 more than the other. If the two parts are in the ratio 5:3, find the number and the two parts.
Solution:
If a number is divided into two parts in he ratio of 5 : 3, let the parts be 5x, 3x say.
According to the sum,
5x = 3x + 10
⇒ 5x – 3x = 10
⇒ 2x = 10
∴ x = \(\frac { 10 }{ 2 }\)
∴ x = 5
∴ The required number be
x + 3x = 8x
= 8 × 5 = 40
And the parts of number are
5 = 5 × 5 = 25
3 = 3 × 5 = 15
![]()
Question 5.
When I triple a certain number and add 2, I get the same answer as I do when I subtract the number from 50. Find the number.
Solution:
Let the number be x’ say.
3 times of a number = 3 × x = 3x
If 2 is added to 3x then 3x + 2
If ‘xis subtracted from 50 then it becomes 50 – x.
According to the sum,
3x + 2 = 50 – x
3x + x = 50 – 2
4x = 48 .
x = 12
∴ The required number 12
Question 6.
Mary is twice older than her sister. In 5 years time, she will be 2 years older than her sister. Find how old are they both now.
Solution:
Let the age of Marys sister = x say.
Mary’s age = 2 × x = 2x
After 5 years her sister’s age
= (x + 5) years
After 5 years Mary’s age
= (2x + 5) years
According to the sum,
2x + 5 = (x + 5) + 2
= 2x – x = 5 + 2 – 5
∴ The age of Mary’s sister = x = 2 years
Mary’s age = 2x = 2 x 2 = 4 years
![]()
Question 7.
In 5 years time, Reshma will be three times old as she was 9 years ago. How old is she now?
Solution:
Reshma’s present age = ‘x’ years say.
After 5 years Reshmats age
= (x + 5) years
Before 9 years Reshma’s age
=(x – 9) years
According to the sum
= x+ 5 = 3(x – 9) = 3x – 27
x – 3x = -27-5
-2x = -32
x = \(\frac{-32}{-2}\) = 16
∴ x = 16
∴ Reshma’s present age = 16 years.
![]()
Question 8.
A town’s population increased by 1200 people, and then this new population decreased 11%. The town now had 32 less people than it did before the 1200 increase. Find the original population.
Solution:
Let th population of a town after the increase of 1200 is x say.
11% of present population

The present population of town
= 11,200 – 1200 = 10,000
![]()
Question 9.
A man on his way to dinner shortly after 6.00 p.m. observes that the hands of his watch form an angle of 110°. Returning before 7.00 p.m. he notices that again the hands of his watch form an angle of 1100. Find the number of minutes that he has been away.
Solution:
Let the number be ‘x ray.
\(\frac { 1 }{ 3 }\) rd of a number = \(\frac { 1 }{ 3 }\) x x = \(\frac { x }{ 3 }\)
\(\frac { 1 }{ 5 }\) th of a number = \(\frac { 1 }{ 5 }\) x x = \(\frac { x }{ 5 }\)
According to the sum
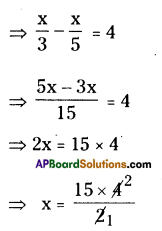
∴ x = 30
∴ The required number is 30.