SCERT AP 8th Class Maths Solutions Chapter 3 చతుర్భుజాల నిర్మాణాలు Ex 3.6 Textbook Exercise Questions and Answers.
AP State Syllabus 8th Class Maths Solutions 3rd Lesson చతుర్భుజాల నిర్మాణాలు Exercise 3.6
కింది ఇవ్వబడిన కొలతలతో కావల్సిన చతుర్భుజాలు నిర్మించండి.
(a) CART రాంబలో CR = 6 సెం.మీ., AT = 4.8 సెం.మీ.
సాధన.
నిర్మాణ క్రమం :
1. 6 సెం.మీ. వ్యాసార్ధంతో \(\overline{\mathrm{CR}}\) కర్ణాన్ని నిర్మించితిని.
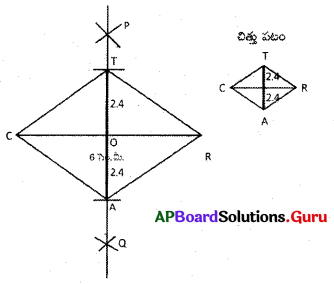
2. \(\overline{\mathrm{CR}}\) వ్యాసార్ధంలో సగం కంటే ఎక్కువ వ్యాసార్ధం తీసుకొని, C, R కేంద్రాల నుండి పైన, క్రింద గీచిన చాపాల ఖండన బిందువులు P, Q లుగా గుర్తించవలెను. P, Qలను కలుపగా CRకు లంబ సమద్విఖండన రేఖ ఏర్పడినది. వీటి ఖండన బిందువును ‘O’ గా గుర్తించితిని.
3. AT = 4.8 సెం.మీ. వ్యాసార్ధంలో సగం వ్యాసార్ధం 2.4 సెం.మీ.లతో ‘O’ కేంద్రంగా రెండు చాపాలను పైన క్రింద గీయగా అవి లంబ సమద్విఖండన రేఖ \(\overline{\mathrm{PQ}}\)ను A, T ల వద్ద ఖండించుకొనును.
4. C, T లను, C, A లను, R, T లను, R, A లను కలిపితిని.
∴ CART రాంబస్ ఏర్పడినది.
(b) SOAP రాంబస్ లో SA = 4.3 సెం.మీ., OP = 5 సెం.మీ.
సాధన.
నిర్మాణ క్రమం :
1. 4.3 సెం.మీ. వ్యాసార్ధంతో \(\overline{\mathrm{SA}}\) రేఖాఖండాన్ని నిర్మించితిని.
2. 4.3 సెం.మీ. వ్యాసార్ధంలో సగానికంటే ఎక్కువ వ్యాసార్ధంతో S, Aల నుండి పైన క్రింద చాపాలను గీయగా, వాటి ఖండన బిందువులు X, Y లుగా గుర్తించితిని. X, Y లను కలిపితిని.
3. \(\overline{\mathrm{XY}}\), \(\overline{\mathrm{SA}}\) కు ఒక లంబ సమద్విఖండన రేఖ. వీటి ఖండన బిందువును ‘M’ గా గుర్తించితిని.
4. ‘M’ కేంద్రంగా OP వ్యాసార్ధంలో సగం వ్యాసార్ధం 2.5 సెం.మీ.లతో పైన క్రింది గీచిన చాపాలు O, P లవద్ద \(\overline{\mathrm{XY}}\) ను ఖండించినవి.
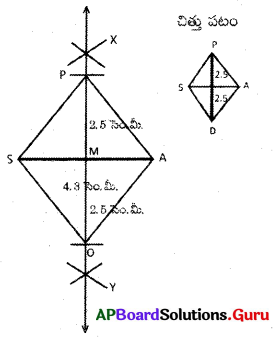
5. S, P లను S, Oలను మరియు P, Aలను, O, A లను కలిపితిని.
6. ∴ SOAP రాంబస్ ఏర్పడినది.
![]()
(c) JUMP చతురస్రంలో కర్ణం 4.2 సెం.మీ.
సాధన.
JM = UP = 4.2 సెం.మీ.
[∵ చతురస్రంలోని కర్ణాలు సమానాలు]
నిర్మాణ క్రమం :
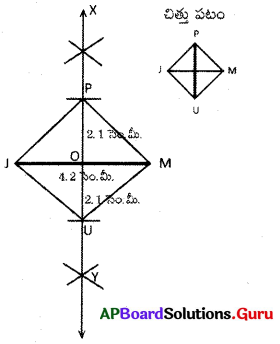
1. 4.2 సెం.మీ. వ్యాసార్ధంతో \(\overline{\mathrm{JM}}\) రేఖాఖండాన్ని (కర్ణం) నిర్మించితిని.
2. \(\overline{\mathrm{JM}}\) వ్యాసార్ధంలో సగాని కంటే ఎక్కువ వ్యాసార్ధంతో J, M కేంద్రాల నుండి పైన, క్రింద గీచిన చాపాల ఖండన బిందువులను X, Y లుగా గుర్తించితిని.
3. X, Y లను కలిపితిని. \(\overline{\mathrm{XY}}\), \(\overline{\mathrm{JM}}\) కు ఒక లంబ సమద్విఖండన రేఖ. ఇది \(\overline{\mathrm{XY}}\) ను ‘O’ వద్ద ఖండిస్తుంది.
4. ‘O’ కేంద్రంగా \(\overline{\mathrm{UP}}\) వ్యాసార్ధంలో సగం వ్యాసార్థంతో పైన, క్రింద గీచిన చాపాలు \(\overline{\mathrm{XY}}\) ను U, Pల వద్ద ఖండించును.
5. J, U లను, U, M లను మరియు J, P లను, M, P లను కలిపితిని.
∴ చతురస్రం JUMP ఏర్పడినది.