AP Board 8th Class Maths Solutions Chapter 6 వర్గమూలాలు, ఘనమూలాలు Ex 6.3

SCERT AP 8th Class Maths Solutions Chapter 6 వర్గమూలాలు, ఘనమూలాలు Ex 6.3 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 6th Lesson వర్గమూలాలు, ఘనమూలాలు Exercise 6.3

ప్రశ్న1.
భాగహార పద్ధతిన వర్గమూలాలు కనుక్కోండి.
(i) 1089
సాధన.

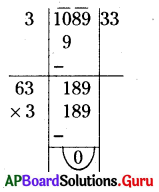
∴ \(\sqrt{1089}\) = 33

(ii) 2304
సాధన.

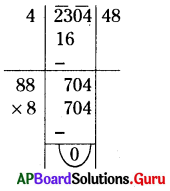
∴ \(\sqrt{2304}\) = 48

(iii) 7744
సాధన.

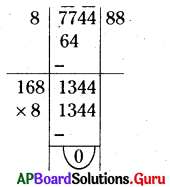
∴ \(\sqrt{7744}\) = 88

(iv) 6084
సాధన.

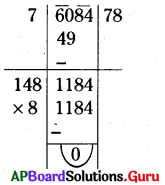
∴ \(\sqrt{6084}\) = 78

(v) 9025
సాధన.

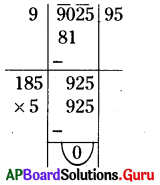
∴ \(\sqrt{6084}\) = 78

ప్రశ్న2.
క్రింది దశాంశాలకు వర్గమూలాలను కనుక్కోండి.
(i) 2.56
సాధన.

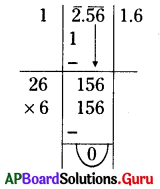
∴ \(\sqrt{2.56}\) = 78

(ii) 18.49
సాధన.

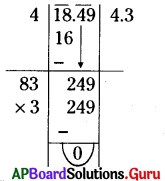
∴ \(\sqrt{18.49}\) = 4.3

(iii) 68.89
సాధన.

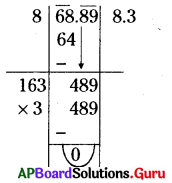
∴ \(\sqrt{68.89}\) = 8.3

(iv) 84.64
సాధన.

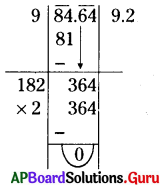
∴ \(\sqrt{84.64}\) = 9.2

ప్రశ్న3.
4000 నుండి ఏ కనిష్ఠ సంఖ్యను తీసివేసిన పరిపూర్ణ వర్గం అగును ?
సాధన.
4000 నుండి ఒక కనిష్ఠ సంఖ్యను తీసివేయవలెనన్న భాగహార పద్ధతిన వర్గమూలం కనుగొనవలె.

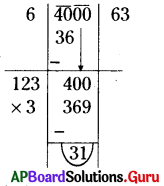
∴ 4000 నుండి ’31’ అను కనిష్ఠ సంఖ్యను తీసివేసిన పరిపూర్ణ వర్గం అగును.

ప్రశ్న4.
ఒక చతురస్ర వైశాల్యం 4489 సెం.మీ.² అయిన భుజం పొడవు ఎంత ?
సాధన.
చతురస్ర వైశాల్యం (A) = 4489 సెం.మీ.²
∴ A = s²
⇒ s² = \(\sqrt{4489}\) = \(\sqrt{67 \times 67}\) = 67 సెం.మీ.
చతురస్ర భుజం (s) = 67 సెం.మీ.

ప్రశ్న5.
ఒక తోటమాలి 8289 మొక్కలను చతురస్రాకారంలో కొన్ని వరుసలలో నాటాడు. నాటిన తరువాత 8 మొక్కలు మిగిలిన ప్రతి వరుసలో నాటిన మొక్కలు ఎన్ని ?
సాధన.
మొత్తం నాటిన మొక్కలు = 8289
8289 మొక్కలను చతురస్రాకారంలో నాటగా 8మొక్కలు మిగిలిపోగా నాటిన మొక్కలు = 8289 – 8
= 8281
ఒక్కొక్క వరుసలో నాటిన మొక్కల సంఖ్య కావలెనన్న 8281 కు వర్గమూలం కనుగొనవలెను.

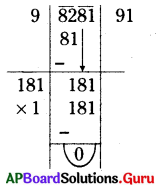
∴ 8281 మొక్కలను చతురస్రాకారంగా నాటగా ప్రతి వరుసకు వచ్చు మొక్కల సంఖ్య = 91

ప్రశ్న6.
కనిష్ఠ నాలుగు అంకెల పరిపూర్ణ వర్గ సంఖ్యను కనుగొనుము.
సాధన.
నాలుగు అంకెల కనిష్ఠ సంఖ్య = 1000

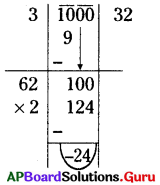
∴ 1000 కు 24 ను కలిపిన 1000 + 24 = 1024
∴ నాలుగు అంకెల కనిష్ఠ పరిపూర్ణ వర్గసంఖ్య = 1024

ప్రశ్న7.
6412 కు ఏ కనిష్ఠ సంఖ్యను కలిపిన పరిపూర్ణ వర్గసంఖ్య అగును ?
సాధన.

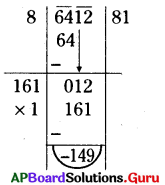
∴ 6412 కు 149 అను కనిష్ఠ సంఖ్యను కలిపిన పరిపూర్ణ వర్గసంఖ్య అగును.

ప్రశ్న8.
క్రింది వాటి వర్గమూలాలను దగ్గరి పూర్ణాంకానికి అంచనా వేసి చెప్పండి.
(i) \(\sqrt{97}\)
సాధన.
97, వర్గ సంఖ్యలయిన 81 మరియు 100 ల మధ్య ఉండును.
81 < 97 < 100
⇒ 9² < 97 < 10²
⇒ 9 < \(\sqrt{97}\) < 10
∴ \(\sqrt{97}\) విలువ 10 కి. దగ్గరగా ఉండవచ్చు.
[∵ 97, 100 కు దగ్గరగా ఉన్నది.]

(ii) \(\sqrt{250}\)
సాధన.
250 వర్గ సంఖ్యలైన 225, 256 ల మధ్య ఉండును.
∴ 225 < 250 < 256
⇒ 15² < 250 < 16²
= 15 < \(\sqrt{250}\) < 16
∴ 250 విలువ 16 కు దగ్గరగా ఉండవచ్చు.
[∵ 250, 256 కు దగ్గరగా ఉన్నది.]

(iii) \(\sqrt{780}\)
సాధన.
780, వర్గ సంఖ్యలైన 729 మరియు 784 ల మధ్య కలదు.
∴ 729 < 780 < 784
⇒ 27² < 780 < 28²
⇒ 27 < \(\sqrt{780}\) < 28
∴ \(\sqrt{780}\), 28 కు దగ్గరగా ఉండును.
[∵ 780, 784 కు దగ్గరగా ఉన్నది.]