Practice the AP 10th Class Maths Bits with Answers Chapter 13 Probability on a regular basis so that you can attempt exams with utmost confidence.
AP SSC 10th Class Maths Bits 1st Lesson Chapter 13 Probability with Answers
Question 1.
Karishma and Reshma are playing chess. The probability of winning Karishma is 0.59. Then find probability of Reshma winning the match.
Answer:
0.41
Explanation:
Reshma winning match = 1 – 0.59
= 0.41
Question 2.
Vineeta said that probability of impos-sible events is 1. Dhanalakshmi said that probability of sure event is ‘0’ and Sireesha said that probability of any event lies in between 0 and 1. In the above with whom will you agree?
Answer:
Sireesha
Question 3.
A page is opened at a random from a book containing 90 pages. Then find the probability of a page number is a perfect square.
Answer:
\(\frac{1}{90}\)
Explanation:
\(\frac{\text { Required page }}{\text { Total pages }}\) = \(\frac{1}{90}\)
Question 4.
From the figure, find the probability of getting blue ball.
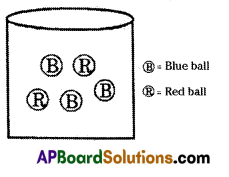
Answer:
\(\frac{3}{5}\)
Explanation:
\(\frac{\text { No. of blue balls }}{\text { Total balls }}\) = \(\frac{3}{5}\)
Question 5.
Find the probability of picking a red king card from a well shuffled deck of playing cards.
Answer:
\(\frac{1}{26}\)
Question 6.
Find the probability of getting a head when a coin is tossed once.
Answer:
\(\frac{1}{2}\)
![]()
Question 7.
Write any one value which cannot be the probability of an event?
Answer:
-1.5
Question 8.
If P(E) = 0.26, then find P (\(\overline{\mathbf{E}}\)).
Answer:
0.74
Question 9.
Find probability of getting 7, when a dice is rolled.
Answer:
0
Question 10.
Which of the following situations have equally likely events?
Answer:
Getting 1 or 2 or 3 or 4 or 5 or 6 when a dice is rolled and winning or loosing a game and Head or Tail, when a coin is tossed.
Question 11.
The probability of picking a letter from the set of english alphabets is \(\frac{5}{26}\). Find that alphabet can be.
Answer:
Vowel
Explanation:
In English letters 5 vowels are there.
So the probability is \(\frac{5}{26}\)
Question 12.
If a die is rolled, then find the probability of getting a prime number.
Answer:
\(\frac {1}{2}\)
Question 13.
Which of the following cannot be the probability of an event?
Answer:
1.\(\overline{3}\)
![]()
Question 14.
IfP(E) = 1, then p(\(\overline{\mathbf{E}}\)).
Answer:
0
Question 15.
When a die is rolled, find the probability of getting an odd prime number.
Answer:
\(\frac{1}{3}\)
Question 16.
Find the probability that the sum of two numbers appearing on the top of the dice is 13, when two dice are rolled at the same time.
Answer:
0
Question 17.
If P(E) = 0.05, then find P(\(\overline{\mathbf{E}}\)).
Answer:
0.95
Question 18.
Which of the following be the probability of an event?
– 1.5, 2.4, 0.7, 115%
Answer:
0.7
Question 19.
P(E) = 0.65, then find P(\(\overline{\mathbf{E}}\)).
Answer:
0.35
Question 20.
If P(E) = 0.82, then find P(\(\overline{\mathbf{E}}\))
Answer:
0.18
![]()
Question 21.
On random selection, find the probability of getting a composite number among the numbers from 51 to 100.
Answer:
\(\frac{4}{5}\)
Question 22.
Let E and \(\overline{\mathbf{E}}\) be the complementary events. If P(\(\overline{\mathbf{E}}\)) = 0.65, then find P(E).
Answer:
0.35
Explanation:
P(E) = 1 – P(E)
⇒ 0.65 = 1 – P(E)
⇒ P(E) = 1 – 0.65 = 0.35
Question 23.
At what value of ‘x’, \(\frac{5}{x}\) may possible, probability of an event?
Answer:
6
Question 24.
If P(E) is the probability of an event E, then write the relation.
Answer:
0 ≤ P(E) ≤ 1
Question 25.
The probability of getting right answer to a question is 0.68, then find the probability of getting a wrong answer.
Answer:
0.32 (or) 32%
Question 26.
In a single throw of two dice, find the probability of getting distinct numbers.
Answer:
\(\frac{5}{6}\)
Question 27.
Find the value of P(E) – 1 + P(\(\overline{\mathbf{E}}\)) .
Answer:
0
![]()
Question 28.
Getting a prime (or) composite number is example to event.
Answer:
Mutually exclusive event.
Question 29.
P(G) = \(\frac{4}{17}\) then find p(\(\overline{\mathbf{G}}\)).
Answer:
\(\frac{13}{17}\)
Question 30.
From a well shuffled pack of cards, a card is drawn at random, then find the probability of getting a red jack.
Answer:
\(\frac{1}{26}\)
Question 31.
Find the probability of raining in a day.
Answer:
\(\frac{1}{2}\)
Question 32.
P(E) = 0.45, then find P(\(\overline{\mathbf{E}}\)) .
Answer:
0.545
Question 33.
There are 50 cards numbered from 1 to 50. A card is drawn at random, then find the probability that the number on the card is divisible by 8.
Answer:
\(\frac{3}{25}\)
Explanation:
From 1 to 50 numbers 8 multiples are 8, 16, 24, 32, 40, 48
∴ Required probability = \(\frac{6}{50}=\frac{3}{25}\).
Question 34.
In a simultaneous toss to two coins, find the probability of at least one head.
Answer:
3/4
![]()
Question 35.
The set of all possible events is called
Answer:
Sample space
Question 36.
In a lucky dip of 30 tokens, Gopi purchased two tokens. Then find the probability of getting the first prize.
Answer:
17/26
Question 37.
Two fair dice are rolled and the face values are added. Find the probability of getting an odd number greater than 8.
Answer:
\(\frac{1}{6}\)
Question 38.
Two dice are thrown once together. What is the probability of getting a doublet?
Answer:
\(\frac{1}{6}\)
Question 39.
P(E) + P(\(\overline{\mathbf{E}}\)) is equals to
Answer:
1
Question 40.
When a coin is tossed, find the probability of getting a tail or head.
Answer:
\(\frac{1}{2}\)
Question 41.
P(Impossible event) is equal to
Answer:
0
![]()
Question 42.
P(Sure event) is equal to
Answer:
1
Question 43.
If one side is chosen at random from the sides of a right triangle, then find the probability that it is hypotenuse.
Answer:
1/3
Question 44.
In a box, there are 28 marbles of which ‘x’ are green and the rest are white. If the probability of getting a green marble is \(\frac{2}{7}\), then find the number of green marbles.
Answer:
8
Explanation:
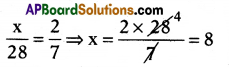
∴ No. of green marbles = x = 8.
Question 45.
How many cards in a pack of playing cards?
Answer:
52
Question 46.
Getting a Tail or Head ……………..event.
Answer:
Equally likely
Question 47.
Find the probability of an event lies between …………… and …………..
Answer:
0,1
Question 48.
A card is pulled from a deck of 52 cards. Find the probability of obtaining a club.
Answer:
1/4
Question 49.
In a single throw of two dice, find the probability of getting even doublet.
Answer:
1/12
![]()
Question 50.
When a dice is rolled, find the probability of getting a composite number.
Answer:
1/3
Question 51.
When a coin is tossed, find the probability of getting a head.
Answer:
1/2
Question 52.
If a coin is tossed, then find the prob-ability that a head turns up.
Answer:
1/2
Question 53.
A box contains pencils and pens. The probability of picking out a pen at random is 0.65. Then find the probability of not picking a pen.
Answer:
0.35
Question 54.
In a single throw of two dice, find the probability of getting a total of 12.
Answer:
\(\frac{1}{36}\)
Question 55.
From a bag containing 6 red balls, 5 green balls and 3 blue balls, find the probability of getting a green ball at random.
Answer:
5/14
Question 56.
If a card is drawn from a pack, find the probability that it is a king.
Answer:
\(\frac{1}{13}\)
![]()
Question 57.
Getting a red card (or) black card is …………… event.
Answer:
Mutually exclusive.
Question 58.
When a dice is thrown, find the probability of getting neither a prime nor composite number.
Answer:
1/6
Question 59.
If E is an event whose probability is
\(\frac{2}{5}\), then find the probability of not E.
Answer:
3/5
Question 60.
Probability of switching on a bulb in a dark room is 0.35, then find the probability of not switching the bulb.
Answer:
0.65
Question 61.
Find the probability of a certain event.
Answer:
1
Question 62.
Find the probability that a leap year has 53 Sundays.
Answer:
2/7
Question 63.
Three different greeting cards and their corresponding covers are randomly-strewn about on a table. If Sita puts the greeting cards into the covers at random, find the probability of correctly matching of all the greeting cards and covers.
Answer:
\(\frac{1}{6}\)
![]()
Question 64.
In a simultaneous toss of two coins, find the probability of no tails.
Answer:
3/4
Question 65.
If a ball is drawn at random from a box containing 11 red balls, 6 white balls and 9 green balls, then find the probability that the ball is not green.
Answer:
\(\frac{17}{26}\)
Question 66.
From a deck of cards, a card is drawn at random, then find the probability of getting a black face card.
Answer:
\(\frac{3}{26}\)
Question 67.
If two dice are rolled at a time, then find the probability that the two faces show different numbers.
Answer:
5/16
Question 68.
Find the probability of a face card from red cards.
Answer:
3/13
Question 69.
A dice is tossed once, then find the probability of getting an even number or a multiple of 3.
Answer:
2/3
Question 70.
The event which can’t happen at all is known as …………….. event.
Answer:
Impossible
![]()
Question 71.
A baby is born, find the probability that it is a boy (or) girl.
Answer:
1/2
Question 72.
If an unbiased coin is tossed, find the probability of getting a tail.
Answer:
1/2
Question 73.
In a single throw of two dice, find the probability of getting a doublet.
Answer:
1/6
Question 74.
Find the probability of getting two tails when two coins are tossed.
Answer:
1/4
Question 75.
From a well shuffled pack of cards a card is drawn at random, then find the probability of getting a red coloured card.
Answer:
1/2
Question 76.
If a die is rolled, then find the probability of getting an even number.
Answer:
1/2
Question 77.
If two dice are rolled simultaneously, then find the sum with greatest possibility to happen.
Answer:
7
Question 78.
When two dice are rolled, find probability of getting odd doublet.
Answer:
1/12
![]()
Question 79.
Find the probability of an impossible event.
Answer:
0
Question 80.
Find the probability of getting a number less than 5 when a die is rolled.
Answer:
2/3
Question 81.
In a single throw of two dice, find the probability of getting a total of 11.
Answer:
1/18
Question 82.
Find the probability of drawing a black card from the black cards.
Answer:
1
Question 83.
If a card is drawn from a deck of 52 cards find the probability that it is a club card.
Answer:
1/4
Question 84.
Two dice are rolled, find the probability of getting 6 as the product.
Answer:
1/9
Question 85.
If the occurrence of one event prevents the occurrence of another event, then which type of element they are?
Answer:
Mutually exclusive.
![]()
Question 86.
In a single throw of two dice, find the probability of getting a total of 3 or 5.
Answer:
1/6
Question 87.
If two dice are thrown simultaneously, find the probability of showing the same numbers on their faces.
Answer:
1/6
Question 88.
Find the probability of drawing a black king from the deck.
Answer:
\(\frac{1}{26}\)
Question 89.
Find the event of getting a number less than or equal to 6.
Answer:
Sure event
Question 90.
If two events have same chances to happen, then they are called which type of events?
Answer:
Equally likely events.
Choose the correct answer satisfying the following statements.
Question 91.
Statement (A): The probability of winning a game is 0.4, then the probability of losing it is 0.6.
Statement (B) : P(E) + P(not E) = 1
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
i) Both A and B are true.
Question 92.
Statement (A) : When two coins are tossed simultaneously, then the probability of getting no tail is \(\frac{1}{4}\).
Statement (B): The probability of getting a head (i.e., no tail) in one toss of a coin is \(\frac{1}{2}\).
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
i) Both A and B are true.
![]()
Question 93.
Statement (A) : Card numbered as 1, 2, 3, ………….., 15 are put in a box and mixed thoroughly, one card is then drawn at random. The probability of drawing an even number is \(\frac{1}{2}\).
Statement (B) : For any event E, we have 0 ≤ P(E) ≤ 1.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
iii) A is false, B is true.
Question 94.
Statement (A) : In a simultaneously throw of a pair of dice. The probability of getting a double is \(\frac{1}{6}\) .
Statement (B): Probability of an event may be negative.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
ii) A is true, B is false.
Question 95.
Statement (A): The probability of getting a prime number. When a die is
thrown once is \(\frac{2}{3}\).
Statement (B) : Prime numbers on a die are 2, 3, 5.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
iii) A is false, B is true.
Question 96.
Statement (A) : If P(A) = 0.3 and P(A∪\(\bar{B}\))= 0.8, then P(B) is \(\frac{2}{7}\).
Statement (B): P(\(\overline{\mathbf{E}}\)) = 1 – P(E), where E is any event.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
i) Both A and B are true.
Question 97.
Statement (A): If P(A) = 0.25, P(B) = 0.50 and P(A∩B) = 0.14, then the probability that either A or B occurs is 0.39.
Statement (B) : \(\overline{\mathrm{A} \cup \mathrm{B}}=\overline{\mathrm{A}} \cup \overline{\mathrm{B}}\)
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
iii) A is false, B is true.
Question 98.
Statement (A) : If A and B are two independent events and it is given that
P(A) = \(\frac{2}{5}\), P(B) = \(\frac{3}{5}\) , then P(A∩B) = \(\frac{6}{25}\).
Statement (B) : P(A∩B) =P(A).P(B), where A and B are two independent events.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
i) Both A and B are true.
Question 99.
Statement (A) : If a box contains, 5 white, 2 red and 4 black marbles, then the probability of not drawing a white marble from the box is \(\frac{5}{11}\).
Statement (B): p(\(\overline{\mathbf{E}}\)) = 1 – P(E), where E is any event.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
iii) A is false, B is true.
![]()
Question 100.
Statement (A) : In rolling a dice, the probability of getting number 8 is zero.
Statement (B) : Its an impossible event.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
i) Both A and B are true.
Read the below passages and answer to the following questions.
A die has two faces each with number ‘1’, three faces each with number ‘2’ arid one face with number ‘3’. Die is rolled once.
Question 101.
The probability of obtaining the number 2 is
Answer:
\(\frac{1}{2}\)
Question 102.
The probability of getting the number 1 or 3 is
Answer:
\(\frac{1}{2}\)
Question 103.
The probability of getting the number 3 is
Answer:
\(\frac{5}{6}\)
A student hds a dice whose six faces show the letters A, B, C, D, E and E The dice is thrown once.
Question 104.
What is the probability of getting ‘A’?
Answer:
\(\frac{1}{6}\)
Question 105.
What is the probability of getting ‘D’?
Answer:
\(\frac{1}{6}\)
Question 106.
How many times the experiment was done?
Answer:
Once only
A box contains 3 blue and 4 red balls.
![]()
Question 107.
Find the probability of taken blue ball out.
Answer:
\(\frac{3}{7}\)
Question 108.
Find the probability of taken red ball out.
Answer:
\(\frac{4}{7}\)
A page is opened at random from a book containing 100 pages.
Question 109.
Find the probability that the page number is a perfect square.
Answer:
\(\frac{10}{100}\) = 0.1
Question 110.
Find the probability that the page number is a even number.
Answer:
\(\frac{50}{100}=\frac{1}{2}\)
Question 111.
Find the probability that the page number is a odd number.
Answer:
\(\frac{50}{100}=\frac{1}{2}\)
Observe the given table and answer to the following questions.

Question 112.
Find the probability of selecting ‘B’ blood group student.
Answer:
\(\frac{13}{40}\)
Question 113.
Find the probability of selecting ‘A’ blood group student.
Answer:
\(\frac{10}{40}\)
Question 114.
Find the probability of selecting ‘AB’ blood group student.
Answer:
\(\frac{12}{40}\)
![]()
Question 115.
Find the probability of selecting ‘O’ blood group student.
Answer:
\(\frac{5}{40}=\frac{1}{8}\)
A die is thrown once
Question 116.
Find the probability of getting an even number.
Answer:
1/2
Question 117.
Find the probability of getting an odd prime number.
Answer:
\(\frac{1}{2}\)
Write the correct matching options.
Question 118.

Answer:
A – (iv), B – (v), C – (i)
Question 119.

A – (iii), B – (ii)
Question 120.
Written description Probability

Answer:
A – (ii), B – (i)
Question 121.

Answer:
A – (ii), B – (iv)
![]()
Question 122.

Answer:
A – (ii), B – (i)
Question 123.

Answer:
A – (iv), B – (iii)
Question 124.

Answer:
A – (vi), B – (v)
Question 125.
A card is drawn from a well-shuffled deck of 52 cards randomly. What is the probability of getting a card, which is neither an ace nor a king card?
Answer:
\(\frac{11}{13}\)