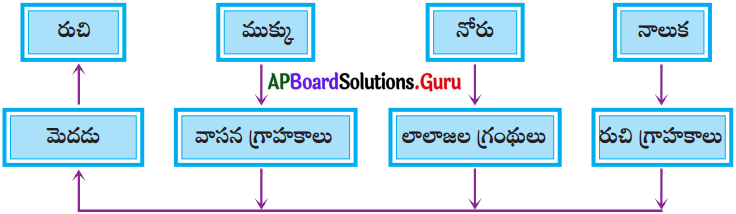
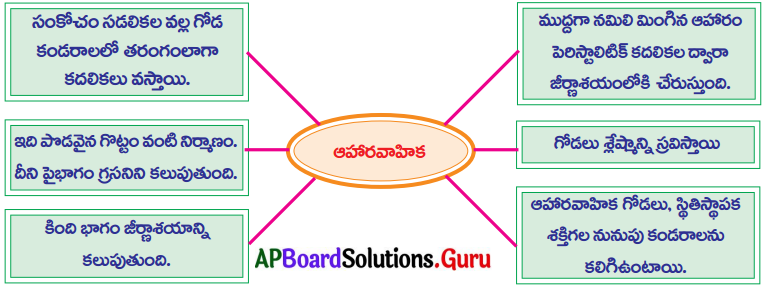
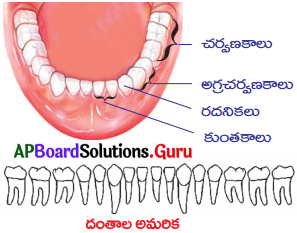
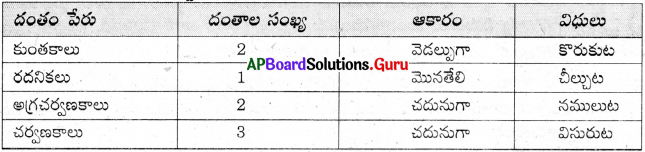
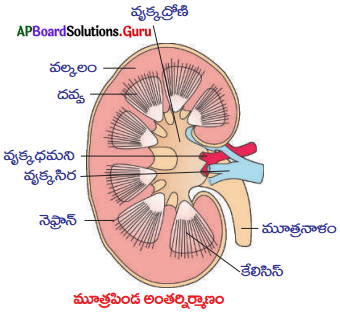
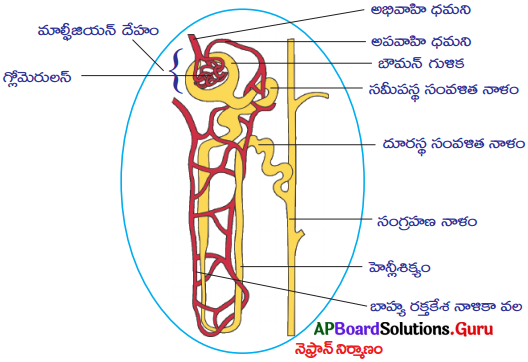
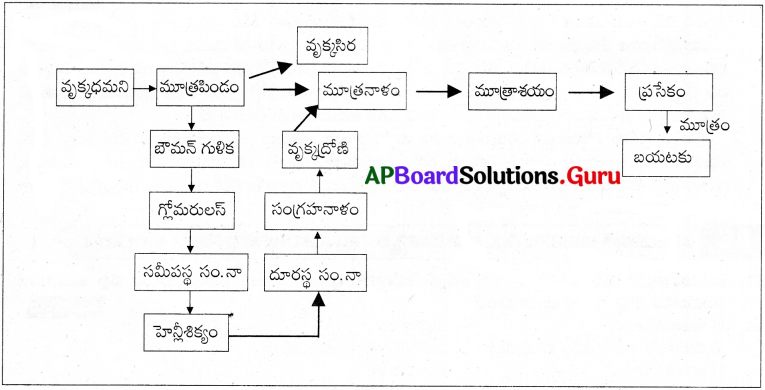
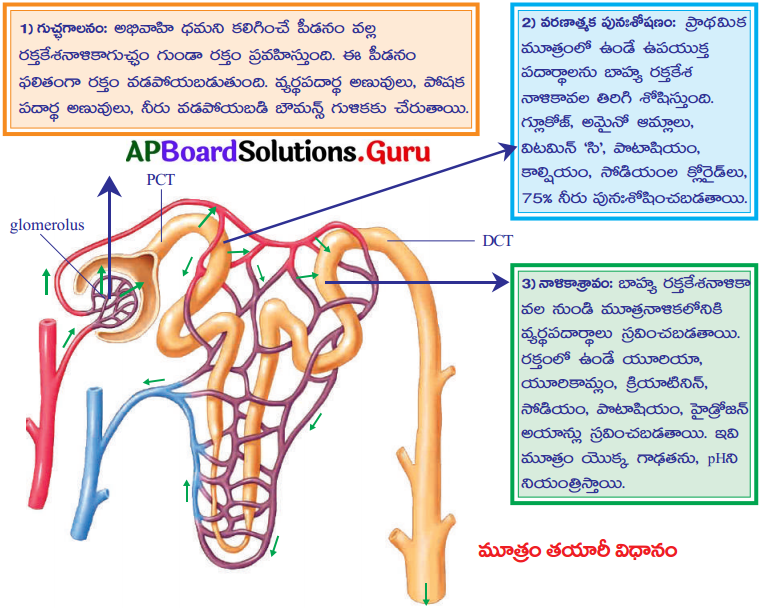
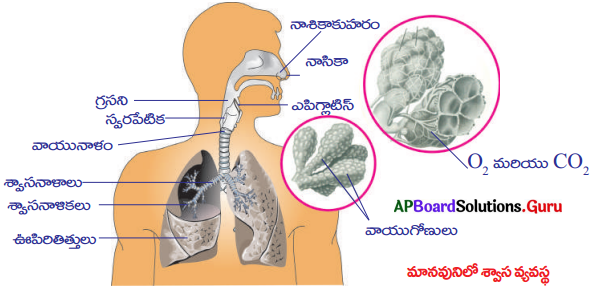
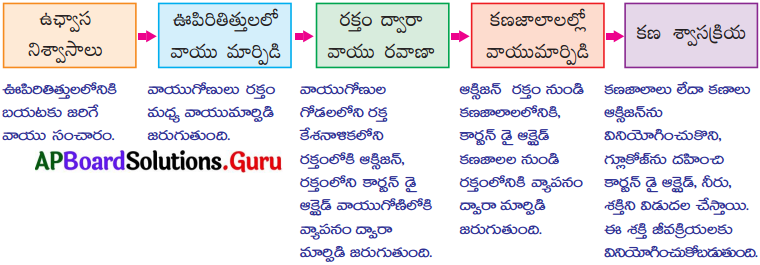
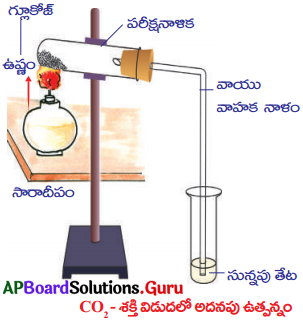
SCERT AP 10th Class Biology Study Material 10th Lesson సహజ వనరులు Textbook Questions and Answers.
AP State Syllabus 10th Class Biology 10th Lesson Questions and Answers సహజ వనరులు
10th Class Biology 10th Lesson సహజ వనరులు Textbook Questions and Answers
అభ్యసనాన్ని మెరుగుపరుచుకోండి
ప్రశ్న 1.
ప్రస్తుతం మీ పరిసరాలలో అతి తక్కువగా అందుబాటులో ఉన్న సహజ వనరు ఏది? అది మీపై ఎలాంటి ప్రభావం చూపుతుంది?
జవాబు:
మా పరిసరాలలో తక్కువగా అందుబాటులో ఉన్న సహజ వనరు నీరు. ఇది నిత్యావసరమైనప్పటికి లభించటం కష్టంగా ఉంది. ప్రధానంగా మంచినీటి కోసం దూర ప్రాంతాలకు ప్రయాణించవలసి వస్తోంది. కావున ప్రాంత ప్రజలు నీటి కొరతను ఎదుర్కొంటున్నారు.
ఎ) అంతకు ముందు లేదా పూర్వం ఈ వనరు అధికంగా ఉండేదా?
జవాబు:
పూర్వపు రోజులలో ఈ ప్రాంతంలో నీటి ఎద్దడి ఉండేది కాదు. అందరికీ పుష్కలంగా నీరు లభించేది. బావుల నిండా నీరు ఉండేది. ఊరందరికీ సరిపడే నీరు లభించేది.
బి) కాలం గడుస్తున్న కొద్దీ ఈ వనరు ఎందుకు తగ్గిపోయింది?
జవాబు:
మారుతున్న ఋతుపవనాల వలన, నీటి వినియోగంలోని నిర్లక్ష్యం వలన నానాటికి భూగర్భ జలాలు క్షీణించాయి. భూగర్భ జలాలు క్షీణించటం వలన బావులు ఎండిపోయి నీటి కొరత ఏర్పడింది.
సి) ఈ వనరులను కాపాడుకోవాలంటే ఏం చేయాలి? (నీవేం చేస్తావు?)
జవాబు:
నీరు అన్ని జీవులకూ జీవనాధారం. నీరు లేకుండా ఏ ప్రాణీ జీవించలేదు. అందువలన నీటి వనరులను సంరక్షించాలి. దీని కోసం
- ఇంకుడు గుంటలు నిర్మించి భూగర్భజలం పెంచాలి.
- ఇంకుడు చెరువులు, చెక్ డ్యామ్లు నిర్మించి నీటిని ఇంకింపచేయాలి.
- వ్యవసాయంలో సూక్ష్మనీటిపారుదల పద్ధతులు వాడాలి.
- వర్షపు నీటి నిల్వకు, చెరువులు, కాలువలు పూడిక తీయించాలి.
ప్రశ్న 2.
ప్రపంచ ఇంధన వనరుల గణాంక వివరాల నివేదిక ప్రకారం 2010 నాటికి ప్రపంచ వ్యాప్తంగా 188.8 మిలియన్ టన్నుల నూనె నిలవలు ఉన్నాయి. ఇవి రాబోయే 46.2 సంవత్సరాలకు మాత్రమే సరిపోతాయి అని తెలియజేశారు. నూనె వనరులను పొదుపుగా ఉపయోగించుకోడానికి నీవు సూచించే చర్యలు ఏమిటీ? పొదుపుగా వాడుకోనట్లయితే జరిగే పరిణామాలు ఏమిటి?
జవాబు:
పెట్రోలు, బొగ్గు వంటి శిలాజ ఇంధనాలు తరిగిపోయే శక్తివనరులు. వీటిని విచక్షణారహితంగా వాడటం వలన త్వరలోనే అయిపోతాయి. కావున వీటి వినియోగంలో పొదుపు అవసరం.
నూనె వనరులను పొదుపుగా వాడటానికి చర్యలు :
- అధిక మైలేజీ ఇచ్చే వాహనాలకు ప్రాధాన్యం ఇవ్వాలి.
- పబ్లిక్ రవాణా వ్యవస్థను వాడాలి.
- చిన్న చిన్న దూరాలకు సైకిళ్లను వాడాలి.
- సోలార్ వాహనాలను అభివృద్ధిపరచాలి.
- విద్యుత్ రంగాన్ని అభివృద్ధి పరచి సరిపడినంత విద్యుత్ ఉత్పత్తి చేసుకోవాలి.
- ప్రత్యామ్నాయ శక్తి వనరులను అభివృద్ధి చేసుకోవాలి.
- బయోడీజిల్, పెట్రో పంటలను ప్రోత్సహించాలి.
- పట్టణాలలో సిటీ సర్వీసులకు బదులు మెట్రోరైల్వే వ్యవస్థను వృద్ధిపరచాలి.
పొదుపుగా వాడకపోతే ఫలితాలు :
- పెట్రోలియం నిక్షేపాలు అన్నీ అయిపోతాయి. అందువలన బొగ్గు, పెట్రోలు వంటి వనరులు లభించవు.
- వాహనాలను, పరిశ్రమలను నడపలేము.
- మానవ జీవితం పూర్తిగా స్తంభించిపోతుంది.
- అభివృది అడుగంటి, వెనుకబడిపోతాము.
- శక్తి సంకటం’ ఏర్పడుతుంది.
- ప్రత్యామ్నాయ శక్తి వనరుల కోసం పోటీ ఏర్పడుతుంది.
ప్రశ్న 3.
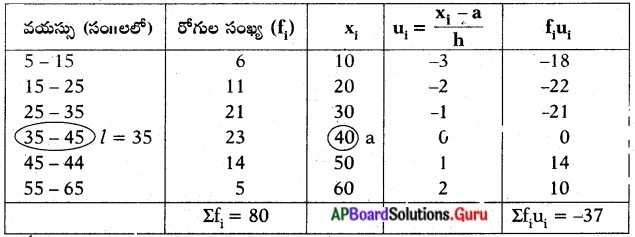
కింద ఇవ్వబడిన సమాచారాన్ని చదివి, దాని కింద ఇవ్వబడిన ప్రశ్నలకు జవాబులివ్వండి.
[ శ్రీకాకుళం జిల్లాలో రెండు మండలాలలోని ఇరవైకి పైగా గ్రామాల నుండి ప్రజలు చేరి, ఒక ప్రైవేటు కంపెనీ సముద్ర తీరంలో తలపెట్టిన ఇసుక తవ్వకాన్ని తీవ్రంగా వ్యతిరేకించారు. ప్రభుత్వం ఈ ప్రాజెక్టును రద్దుచేయకపోతే, వారి పోరును తీవ్రతరం చేస్తామని హెచ్చరించారు. తీరప్రాంతం నుండి విలువైన ఖనిజాలను వెలికితీసే ఉద్దేశంతోనే ఇసుక తవ్వకాన్ని చేపట్టదలిచారు. ఇసుక తవ్వకం మొదలు పెట్టిన అటవీ సరిహద్దు ప్రాంతంలోనే ఈ ప్రజలు నివసిస్తారు.
ఎ) గ్రామ ప్రజలు ఈ విధంగా వ్యతిరేకించి పోరాడడం సరైనదేనా?
జవాబు:
గ్రామ ప్రజల వ్యతిరేక పోరాటం సరైనది.
బి) పోరాడడం వలన గ్రామస్తులు ఏ వనరులను కాపాడుకోగలరు?
జవాబు:
ఈ పోరాటం వలన గ్రామస్తులు విలువైన ఖనిజ వనరులను కాపాడుకోగలరు.
సి) ఇసుక నుండి వెలికితీసిన విలువైన ఖనిజాల వల్ల గ్రామస్తులు ఏమైనా లాభం పొందుతారా?
జవాబు:
ఖనిజ తవ్వకం ప్రైవేటు కంపెనీ చేపట్టింది కాబట్టి, గ్రామస్తులకు లభించే ప్రయోజనం ఏమీ ఉండదు.
డి) తీరప్రాంతంలో ప్రైవేటు కంపెనీ ఎందుకు తవ్వకాలను చేపట్టాలనుకుంది?
జవాబు:
విలువైన ఖనిజాల కోసం ప్రైవేటు కంపెనీ తీర ప్రాంత ఇసుకలో తవ్వకాలను చేపట్టింది.
ఇ) దీనిలో ప్రభుత్వ పాత్ర ఏమిటి?
జవాబు:
ఇటువంటి అక్రమ తవ్వకాలను నిరోధించాల్సిన బాధ్యత ప్రభుత్వం పైన ఉంది. దీనికోసం కఠినమైన చట్టాలు, నిఘా వ్యవస్థను పెంచాలి.
ఎఫ్) ఇసుక తవ్వకం అక్కడి ప్రజల జీవనంపై ఎలాంటి ప్రభావం చూపుతుంది?
జవాబు:
ఇసుక తవ్వకం వలన సముద్ర తీర ఆవాసం దెబ్బతింటుంది. సముద్రం ముందుకు రావడంతో తీరప్రాంత గ్రామాలకు నష్టం కలుగుతుంది. ఇది గ్రామ ప్రజల జీవన విధానాన్ని, ఆవాసాన్ని పాడుచేస్తుంది. కావున వారు తవ్వకాలను వ్యతిరేకించారు.
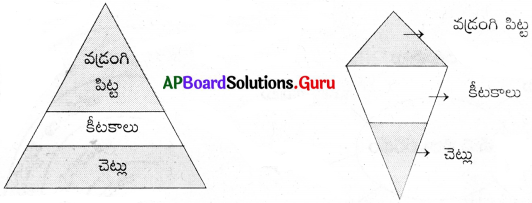
![]()
ప్రశ్న 4.
సుస్థిరాభివృద్ధి అంటే ఏమిటి? వనరుల యాజమాన్యంలో ఏ విధంగా ఉపయోగపడుతుంది?
జవాబు:
అభివృద్ధి, సంరక్షణ రెండింటికి ప్రాధాన్యమిస్తూ, భావితరాలకు అవసరమయ్యే సహజ వనరులను అందుబాటులో ఉండే విధంగా మనం పర్యావరణాన్ని ఉపయోగించుకున్నట్లయితే అది సుస్థిరాభివృద్ధి అవుతుంది.

అభివృద్ధి పేరుతో మనం అడవులను, పరిసరాలను ధ్వంసం చేస్తూ ముందుకు సాగటం మంచి పరిణామం కాదు. దీనివలన భవిష్యత్ లో విపత్కర పరిస్థితులను ఎదుర్కొనవలసి వస్తుంది. చెట్లను నరికి ఎ.సి.లు వాడుకోవటం అభివృద్ధి అవుతుందా? అభివృద్ధితో పర్యావరణం సంరక్షించబడాలి. మనిషి పర్యావరణంలో ఒక ప్రాణి అన్న విషయాన్ని గుర్తుంచుకోవాలి. ఎంత ఎదిగినా ప్రకృతిలో ఒదిగినపుడే తన మనుగడకు క్షేమమని మరచిపో కూడదు. దీనికోసం ప్రకృతి ప్రసాదించిన వనరులను విచక్షణాయుతంగా, పొదుపుగా, పునఃచక్రీయంగా, సమతాస్థితి కాపాడే విధంగా వాడుకోవాలి.
ప్రశ్న 5.
సహజ వనరుల సంరక్షణ – యాజమాన్యంపై వివరంగా రాయండి. .
జవాబు:
సహజ వనరులు మన అవసరాలను తీర్చటానికే గాని అత్యాశకు కాదు’ – అన్న గాంధీ మహాత్ముని వాక్యాన్ని మనం నిరంతరం గుర్తుచేసుకొంటూ, సహజ వనరులను సంరక్షించుకోవాలి. గాలి, నీరు, నేల, అడవి, ఖనిజాలు, సముద్రం, పర్వతాలు ఇవన్నీ సహజ వనరులే. వీటిని విచక్షణారహితంగా వాడుకొంటూ, వృథా చేస్తూ దుర్వినియోగం చేస్తున్నాము. దీని నివారణకు సరైన ‘సహజ వనరుల యాజమాన్యం ‘ ఉండాలి.
- సహజ వనరుల వినియోగంపై రాష్ట్రస్థాయి నుండి దేశీయ, అంతర్జాతీయ స్థాయిలలో స్పష్టమైన ప్రణాళికలతో కూడిన యాజమాన్య సంస్థలు ఉండాలి.
- సహజ వనరుల సంరక్షణకు నిర్దిష్టమైన ప్రణాళిక ఉండాలి.
- సహజ వనరుల వినియోగంలో షరతులు ఉండాలి. వాటిని భంగపరచే వారిపై చర్య ఉండాలి.
- పెట్రోలు వినియోగం వలన CO2 ఏర్పడి గాలి కలుషితం జరుగుతుంది. పెట్రోలు వినియోగం బట్టి మొక్కలు, అడవుల వృద్ధి రేటు ఉండేలా ఆయా దేశాలు చర్యలు చేపట్టాలి.
- పరిశ్రమలు, చమురు కంపెనీలు జల కాలుష్యం కలిగిస్తున్నాయి. ఈ నష్టానికి యాజమాన్యం బాధ్యత వహించేలా చర్యలు తీసుకోవాలి. జల వనరుల కాలుష్యాన్ని పూర్తిగా నివారించాలి.
- నేల సంరక్షణకు గాను ఆధునిక వ్యవసాయ పద్ధతులపై రైతులకు అవగాహన కల్పించాలి.
- ఖనిజ వనరులను పరిమితంగా వాడుతూ, 4R సూత్రం పాటించాలి.
- ప్రత్యామ్నాయ వనరులకు ప్రాధాన్యమివ్వాలి.
ప్రశ్న 6.
స్థానికంగా ఉన్న వనరులను పునర్వినియోగించుకొనే కొన్ని మార్గాలను సూచించండి.
జవాబు:
- ఉపయోగించిన నీటిని పెరటి మొక్కలకు మళ్ళించాలి.
- వర్షపు నీటిని ఇంకుడు గుంటకు మళ్ళించాలి.
- ఎలక్ట్రానిక్ వస్తువులను బాగు చేయించే అవకాశం ఉంటే బాగు చేయించాలి.
- పారేసే వస్తువులను, వేరే విధంగా వాడవచ్చునేమో అని గమనించాలి.
- పాత బట్టలు, వస్తువులు ‘పేదవారికి దానం చేయాలి.
- చెట్ల ఆకులు, ఎండిన కొమ్మలు ఎరువుల తయారీకి వాడాలి.
- నేలలో కుళ్ళే పదార్థాలను వర్మీకంపోస్టు వాడాలి.
- 0% వ్యర్థాల నిర్వహణకు కృషిచేయాలి.
- సోలార్ కుక్కర్లకు, హీటర్లకు ప్రాధాన్యం ఇవ్వాలి.
- వాడేసిన వాటర్ బాటిళ్లలో మొక్కలు పెంచి కిచెన్ గార్డెన్ ను ఏర్పాటుచేయాలి.
ప్రశ్న 7.
అడవులను, వన్యజీవులను ఎందుకు సంరక్షించుకోవాలి?
జవాబు:
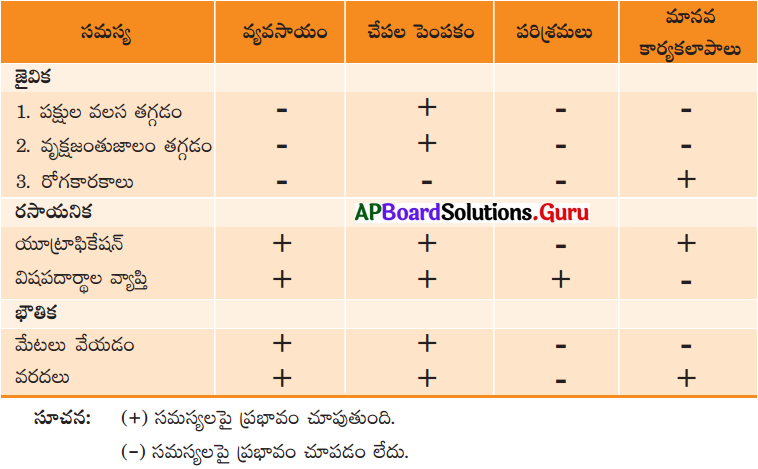
అడవులు ప్రకృతిలో ముఖ్యమైన సహజ వనరులు. భూమి విస్తీర్ణంలో అడవులు 33% ఉండాలి. కానీ మానవ విచక్షణా రహిత చర్యల వలన నేడు ఇవి 19 శాతానికి తగ్గిపోయాయి. ఈ పరిస్థితి కొనసాగితే మానవాళి గొప్ప ప్రమాదాన్ని ఎదుర్కొనవలసి వస్తుంది. ఈ కింది కారణాల వలన మనం అడవులను, వన్యజీవులను కాపాడుకోవాలి.
- అడవులు జీవవైవిధ్యానికి పెట్టింది పేరు. అడవులను నరకటం వలన జీవవైవిధ్యం దెబ్బతిని ప్రకృతి సమతాస్థితి పాడైపోతుంది.
- అడవులు వర్షపాతాన్ని పెంచుతాయి.
- అడవులు నేల క్రమక్షయాన్ని అరికడతాయి.
- అనేక అటవీ ఉత్పత్తులు మానవ జీవనాధారాలు.
- అడవులు అనేక ఖనిజ నిక్షేపాలు కలిగి ఉన్నాయి.
- అడవి ఒక సహజ ఆవాసం.
- ప్రకృతిలోని ప్రతి ప్రాణికీ నిర్దిష్ట పాత్ర ఉంటుంది. అటువంటి కీలకపాత్రను ఆవాసంలో వన్యజీవులు పోషిస్తున్నాయి.
- వన్యప్రాణులు జీన్ బ్యాంలా పనిచేస్తాయి.
- వన్యప్రాణులు అంతరించే ప్రమాదంలో ఉన్నాయి. ఇవి అంతరించటం వలన జీవావాసాలు దెబ్బతింటాయి.
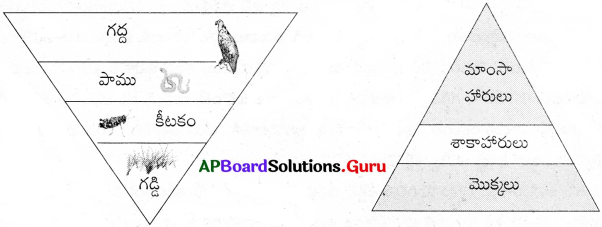
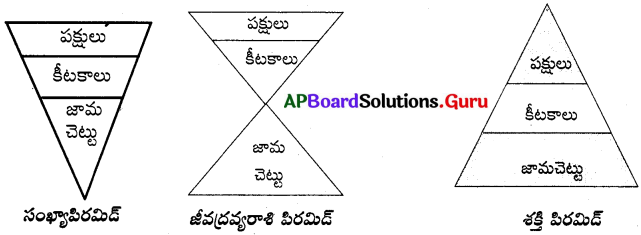
![]()
ప్రశ్న 8.
అడవుల సంరక్షణ విధానాలను కొన్నింటిని సూచించండి.
(లేదా)
“అడవుల సంరక్షణ మన బాధ్యత” దీనికి మీరు పాటించే విధానాలను కొన్నింటిని సూచించండి.
జవాబు:
- అటవీ సంరక్షణ జాతీయ స్థాయి సమస్య. కావున అడవుల సంరక్షణకు, అటవీ శాఖకు మరియు ఇతర శాఖలకు మధ్య మంచి సమన్వయాన్ని పెంచాలి.
- అటవీ సంరక్షణలో ప్రాంతీయ ప్రజల పాత్ర కీలకమైనది. కావున అటవీ సంరక్షణలో వీరిని బాధ్యులుగా చేయాలి.
- చెట్లను నరకటం, తొలగించటం వంటి పనులను పూర్తిగా నిషేధించాలి.
- వన మహోత్సవం’ వంటి కార్యక్రమాలు పెద్ద ఎత్తున చేపట్టి మొక్కలను విరివిగా నాటించాలి.
- పండుగలు, ఉత్సవాల సందర్భాలలో చెట్లను నాటే కార్యక్రమాన్ని అనుసంధానం చేయాలి.
- వంట చెరకు కోసం చెట్లు నరకకుండా ప్రత్యామ్నాయం ఏర్పాటు చేయాలి.
- గడ్డి భూములను సంరక్షిస్తూ చెట్ల పెంపకాన్ని చేపట్టాలి.
- అటవీ సంరక్షణ చట్టం 1980ను కచ్చితంగా అమలు చేయాలి.
- అటవీ సరిహద్దు ప్రాంతాలలో చెక్పన్ల సంఖ్య పెంచాలి.
- అటవీ సంరక్షణకు కృషిచేస్తున్న బృందాలకు ప్రోత్సాహకాలు, బహుమతులు ప్రకటించాలి.
- ఎర్రచందనం, గంధం చెట్లు ఉన్న అడవుల్లో కాపలా పెంచాలి.
- చెట్లను నరకటం, నిర్మూలించటం నేరాలుగా పరిగణించి కఠినమైన శిక్షలు అమలు చేయాలి.
ప్రశ్న 9.
సహజ వనరులు చాలా వేగంగా అంతరించిపోతున్నాయి కదా! దీని వలన జరిగే పరిణామాలను ఊహించండి.
జవాబు:
సహజ వనరులను వేగంగా వినియోగించటం వలన అవి అంతరించిపోయే ప్రమాదం ఉంది. దీనివలన భవిష్యత్తులో బొగ్గు, పెట్రోలు నిల్వలు అడుగంటిపోతాయి. వీటి ఆధారంగా పనిచేసే పరిశ్రమలు, వాహనాలు మూలనపడతాయి. రవాణా వ్యవస్థ స్తంభించిపోతుంది. సమాజం శక్తి కొరతను ఎదుర్కొంటుంది. వాహనాలు లేని సమాజం మధ్యయుగం నాటి పరిస్థితులను ఎదుర్కొంటుంది. చాలా పరిశ్రమలు శక్తి కొరతతో మూలనపడతాయి. వస్తు ఉత్పత్తి తగ్గి, ప్రజల జీవన విధానం దెబ్బతింటుంది. కావున మనం సహజ శక్తి వనరులను పొదుపుగా, విచక్షణతో వాడుకోవాలి.
ప్రశ్న 10.
ఒక పెట్రోలు బంకుకు వెళ్ళి నిర్వాహకుడితో శిలాజ ఇంధనాల వినియోగం గురించి ఇంటర్వ్యూ చేయడానికి ప్రశ్నావళిని రూపొందించండి.
జవాబు:
- పెట్రోలును మీరు ఎక్కడ నుండి కొంటారు?
- ఒక్క రోజులో ఎంత పెట్రోలు విక్రయిస్తారు?
- పెట్రోలు వినియోగం రేటు గతంతో పోల్చితే పెరిగిందా?
- పెట్రోలు వినియోగం రేటు పెరగటానికి కారణం ఏమిటి?
- గతంతో పోల్చితే నేడు పెట్రోలు రేట్లు ఎలా ఉన్నాయి?
- పెట్రోలు రేట్లు ఎందుకు విపరీతంగా పెరుగుతున్నాయి?
- ఇదే పరిస్థితి కొనసాగితే పెట్రోలు వాడకం భవిష్యత్ లో ఎలా ఉంటుంది?
- అందరికీ సరిపడా పెట్రోలు ఉత్పత్తి సాధ్యం అని భావిస్తున్నారా?
- పెట్రోలు వినియోగానికి ప్రత్యామ్నాయం ఏమిటి?
ప్రశ్న 11.
ఇంధన వనరులు, నేలసారం కాపాడటం, వర్షపు నీరు భద్రపరచడం వంటి ఏదైనా ఒక అంశాన్ని ప్రదర్శించటానికి నమూనాను తయారుచేయండి. మీ ఆలోచనలతో నివేదిక రాయంది.
జవాబు:
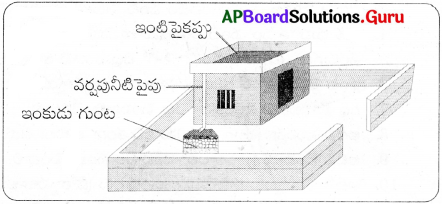
వర్షపు నీటిని భద్రపర్చటంపై నమూనా తయారి:
- ఒక దీర్ఘచతురస్రాకారపు రేకు ముక్కను తీసుకొని, దాని అంచులు మడిచి ఇంటి పై కప్పును రూపొందించాను.
- దీర్ఘచతురస్రాకారపు అట్టముక్కను తీసుకొని దానిని క్రింద అమర్చి, ఇంటి నమూనాను ఏర్పాటు చేశాను.
- ఒక ప్లాస్టిక్ బాటిల్ తీసుకొని దానిలో మట్టి, ఇసుక, కంకరను మూడు పొరలుగా అమర్చి ఇంటి పక్క నేలలో అమర్చాను. ఇది ఇంకుడు గుంట నిర్మాణ ప్రాధాన్యతను చూపుతుంది.
- ఇంటి పై కప్పును కొంచెం వాలుగా అమర్చి వర్షపు నీటిని ఒక మూలకు వచ్చే విధంగా అమర్చాను.
- ఈ వర్షపు నీటిని ఒక పైపు ద్వారా తీసుకొచ్చి ఇంకుడు గుంటకు అమర్చాను.
- తద్వారా వర్షపు నీరు ఇంకుడు గుంటను చేరుతుంది.
ప్రయోజనాలు:
- వర్షపు నీరు ఆదా చేయబడుతుంది.
- భూగర్భజలం పెరుగుతుంది.
- బోరులు, బావులు ఎండిపోవు.
- నీటి కొరత పరిష్కరింపబడుతుంది.
- పరిసర ప్రాంతాలలో నీరు నిలువదు.
- పరిసరాల పరిశుభ్రత కాపాడబడుతుంది.
- ఆరోగ్య సమస్యలు తలెత్తవు.
ప్రశ్న 12.
మీ ప్రాంతంలో సహజ వనరులను పునరుద్ధరించడానికి కృషి చేస్తున్న గ్రామాలు, రైతులు, వారు అనుసరిస్తున్న విధానాలను తెలుసుకొని నివేదిక రాయండి.
జవాబు:
సహజ వనరుల సంరక్షణకు, మా ప్రాంత రైతులకు వ్యవసాయ శాస్త్రవేత్తలు విలువైన సూచనలతోపాటు తగిన సమాచారం ఇచ్చి వాటిని ఆచరించే విధంగా ప్రేరణ ఇచ్చారు. దీనివలన నేల, నీరు యొక్క సంరక్షణ అవసరాన్ని రైతులు తెలుసుకున్నారు. నేల, నీటి సంరక్షణకు రైతులు ఈ కింది పద్ధతులు పాటిస్తున్నారు.
నేల సంరక్షణ :
- రసాయన ఎరువుల స్థానంలో జీవ ఎరువులకు ప్రాధాన్యత.
- వర్మీకంపోస్ట్ వినియోగం, తయారీ.
- లెగ్యుమినేసి పంటలు పండించటం.
- పంట మార్పిడి పద్ధతి పాటించటం.
- అంతర పంటలకు ప్రాధాన్యత.
- నేలసార పరీక్షలు నిర్వహించి తగిన పంటను వేయుట.
- గట్లమీద కంది, బంతి వంటి చిన్న పంటలకు ప్రాధాన్యత.
- వరి స్థానంలో అపరాలవైపు మొగ్గు.
నీటి సంరక్షణ :
- చెరువు పూడిక తీసి నీటి నిల్వ సామర్థ్యం పెంచారు.
- కాలువలోని కలుపు నివారించి నీటి నష్టాన్ని తగ్గించారు.
- ఆరు తడి పంటలకు ప్రాధాన్యత ఇచ్చారు.
- నీరు అందని ప్రాంతాలలో మెట్ట పంటల సాగు.
- ఇంకుడు చెరువు నిర్మించి భూగర్భజల మట్టం పెంచారు.
- చెక్ డ్యామ్లు నిర్మించి నీటి నిల్వలు పెంచారు.
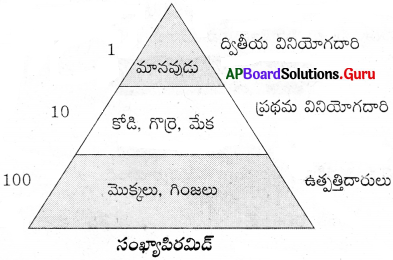
![]()
ప్రశ్న 13.
కాకినాడ వద్ద ONGC వారు చేపట్టిన సహజ వాయువు యొక్క డ్రిల్లింగ్ పనుల గురించి మీరు వినే ఉంటారు. దీనికి సంబంధించిన సమాచారాన్ని సేకరించి, సహజవాయువు ఉత్పత్తిపై నివేదిక రాయండి.
జవాబు:
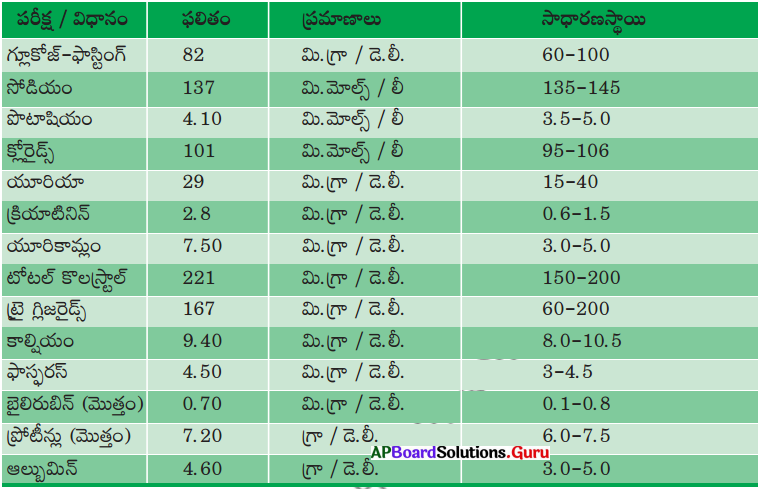
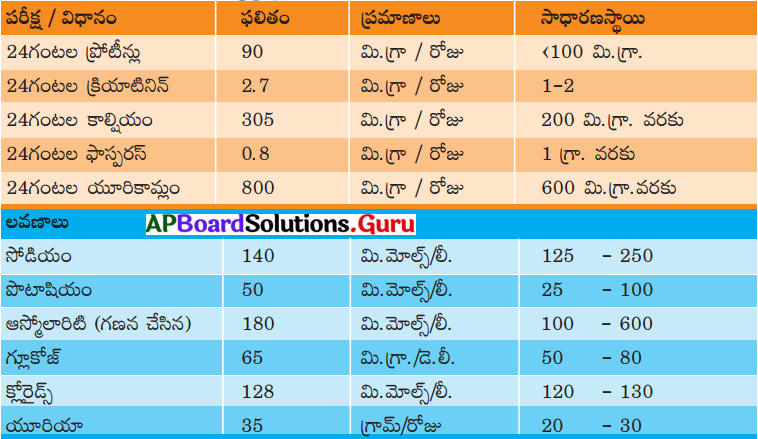
| ఉత్పత్తి | ఆదాయం |
| క్రూడ్ ఆయిల్ | 562.38 బిలియన్ |
| సహజ వాయువు | 168.88 బిలియన్ |
| L.P.G | 31.48 బిలియన్ |
| Naptha | 76.80 బిలియన్ |
| C2 – C3 | 13.44 బిలియన్ |
| SKO | 3.69 బిలియన్ |
Oil and Natural Gas Corporation Limited ను సంక్షిప్తముగా ONGC అంటారు. ఇది దేశీయ స్థాయిలో పేరెన్నిక గన్న ప్రముఖ పెట్రోలు మరియు సహజవాయు కంపెనీ. దీని ప్రధాన కార్యాలయం డెహ్రడూన్లో ఉండగా అనుబంధ కార్యాలయం ఒకటి కాకినాడలో ఉంది.
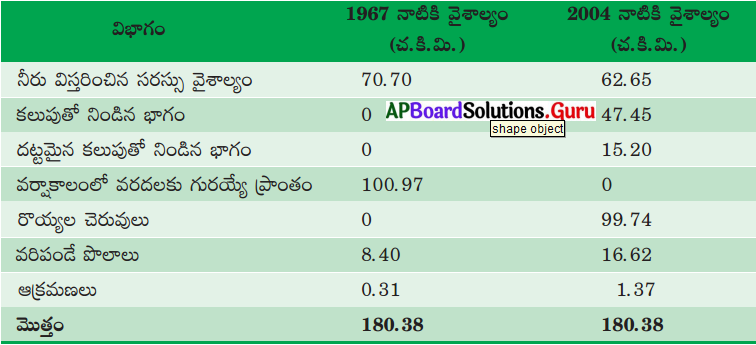
కృష్ణా-గోదావరి బేసిన్ ప్రాంతంలో సహజవాయువు నిక్షేపాలు విస్తారంగా ఉన్నాయని గుర్తించి అక్కడ డ్రిల్లింగ్ ప్రక్రియలు నిర్వహించారు. చాలా మొత్తంలో సహజ వాయువును వెలికితీస్తున్నారు. అయితే ఈ సందర్భంలో సంభవించిన లీకులు మంటలను సృష్టించి ఆ ప్రాంత ప్రజలను భయాందోళనకు గురిచేశాయి. దానితో దీనిని కోనసీమ గుండెలో కుంపటిగా అభివర్ణిస్తూ వచ్చారు.
సహజ వాయువు సేకరణలో కేవలం ఒక్క సహజ వాయువు మాత్రమే లభించదు. అదనంగా అనేక పదార్థాలు లభిస్తాయి. వీటిలో ప్రధానమైనవి-క్రూడ్ ఆయిల్, పెట్రోలియం. పెట్రోలియంను అంశిక స్వేదనం చేయటం వలన కిరోసిన్, డీజిల్, పెట్రోలు, తారు వంటి ఉప ఉత్పత్తులు లభిస్తాయి. ఇవన్నీ ప్రధాన శక్తి వనరులే.
2010లో పెట్రోలియం మరియు సహజవాయువు నియంత్రణ కమిటీ, కాకినాడ వాయు పంపిణీ విధానానికి అవార్డు ప్రకటించింది. GAIL మరియు హిందుస్థాన్ పెట్రోలియం, కాకినాడ పరిసర ప్రాంతాలకు సహజవాయువు సరఫరా కోసం భూఅంతర్భాగ పైపులైను,విధానం ఏర్పర్చింది. దీనివలన కాకినాడ పరిసర ప్రాంతాలైన సామర్లకోట, పెద్దాపురం, పిఠాపురం వంటి ప్రాంతాలకు గ్యాస్ సరఫరా జరుగుతున్నది. పైపు లైను ద్వారా గ్యాస్ సరఫరా జరుగుతున్న మూడవ నగరంగా కాకినాడ పేరు తెచ్చుకొంది. మొదటి రెండు స్థానాలలో హైదరాబాద్, విజయవాడ ఉన్నాయి.
ప్రశ్న 14.
మీ పరిసర ప్రాంతాలలో ఏ పదార్థాన్నెనా పునఃచక్రీయం చేసే యూనిట్లు లేదా పరిశ్రమలు ఉన్నాయా? పదార్థ పునఃచక్రీయం ఎలా జరుగుతుందో రాయండి.
జవాబు:
- మా ప్రాంతంలో ఇనుము పునఃచక్రీయ పరిశ్రమ ఉంది. మిగిలిన వనరులతో పోల్చితే ఇనుము తయారీ కంటే పునఃచక్రీయం సులభం మరియు అవసరము.
- గృహాల నుండి, ప్రధానంగా ఆటోమొబైల్ పరిశ్రమ నుండి వాడి పడేసిన ఇనుప వస్తువులను సేకరిస్తారు.
- సేకరించిన అనుప వస్తువుల నుండి, రస్ట్ తొలగించి, నాణ్యత, మందం, ఆధారంగా విభజన చేస్తారు.
- విభజించిన ఇనుమును అణగగొట్టి పరిమాణం తగ్గించి పరిశ్రమలోనికి రవాణా చేస్తారు.
- ఈ వాడిన ఇనుము పరిశ్రమలోని కొలిమిలో బాగా కరిగించి ద్రవంగా మార్చుతారు.
- కరిగించిన ఇనుమును శుద్ధ ప్రక్రియలో దానిలో ఇతర మలినాలను తొలగిస్తారు.
- తయారీ వస్తువు ఆధారంగా పటుత్వం కొరకు కొన్ని ఇతర లోహాలను కలిపి మిశ్రమ లోహాలను ఏర్పరుస్తారు.
- కరిగించిన ఇనుమును అచ్చులుగా కావాల్సిన ఆకారంలో పోసి వస్తు తయారీకి వాడతారు.
- ఇనుము పునఃచక్రీయం వలన మనకు అవసరమైన ఇనుము దాదాపు 60% ఉత్పత్తి అవుతుంది. అంటే 60% మేర ఇనుప ఖనిజాన్ని ఆదా చేస్తున్నట్లు.
- భూమి నుండి ఖనిజం తవ్వి శుద్ధిచేసి ఇనుమును పొందే ప్రక్రియతో పోల్చితే పునఃచక్రీయ ప్రక్రియ సౌకర్యవంతంగా ఉంటుంది.
ప్రశ్న 15.
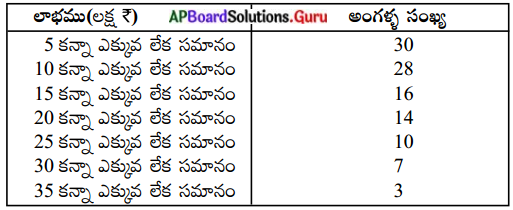
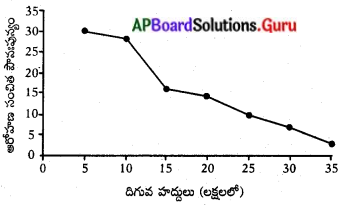
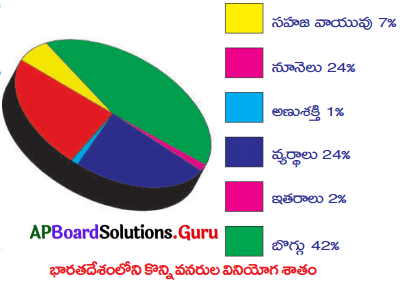
మన దేశంలో పెట్రోలియం వినియోగాన్ని సూచించే ఏదైనా గ్రాను సేకరించి పరిశీలించండి.
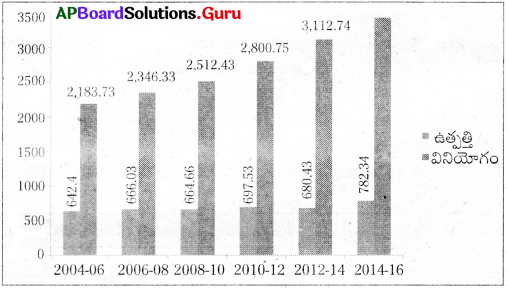
ఎ) మన అవసరాలకు తగినంత ఉత్పత్తి జరుగుతున్నదా?
జవాబు:
లేదు, పెట్రోలియం ఉత్పత్తికంటే వినియోగం అధికంగా ఉంది. కాబట్టి పెట్రోలు కొరత ఏర్పడుతుంది.
బి) ఏ కాలంలో గరిష్ట వినియోగం జరిగింది?
జవాబు:
2008-2010 మధ్యకాలంలో పెట్రోలు వినియోగం రేటు అధికంగా ఉంది.
సి) పది సంవత్సరాల కాలంలో ఉత్పత్తిలో మీరు గమనించిన మార్పు ఏమిటి? (ఉదా : 2004 నుండి 2014)
జవాబు:
పది సంవత్సరాల కాలంలో ప్రజల అవసరాలు తీర్చటం కోసం పెట్రోలియం ఉత్పత్తిని కూడా వృద్ధి చేయటం జరిగింది. అంటే వనరుల వినియోగం రేటు పెరిగింది. ఇది ఇంధన కొరతకు దారితీసే ప్రమాదం ఉంది.
డి) పెట్రోలియం ఉత్పత్తిని పొదుపుగా వాడుకోడానికి మీరు ఇచ్చే సూచనలు ఏమిటి?
జవాబు:
పెట్రోలియం పొదుపుగా వాడటానికి :
- అధిక మైలేజీ ఇచ్చే వాహనాలకు ప్రాధాన్యం ఇవ్వాలి.
- మైలేజీ తగ్గిన వెంటనే వాహనాల ఇంజన్ ఆయిల్ ఫిల్టర్లు సరిచేయించాలి.
- ప్రతి చిన్న అవసరానికి కారు వాడకం మానెయ్యాలి.
- చిన్న చిన్న దూరాలకు సైకిళ్లు వాడాలి.
- పబ్లిక్ ప్రయాణ వాహనాలకు ప్రాధాన్యం ఇవ్వాలి.
- ప్రయాణాన్ని పంచుకోవటం (Shared journey) అలవాటు చేసుకోవాలి.
- వాహనాలను నిర్ణీత వేగంతో నడపాలి.
- ప్రత్యామ్నాయ ఇంధన వనరులకు ప్రాధాన్యం ఇవ్వాలి.
![]()
ప్రశ్న 16.
సహజ వనరులను సద్వినియోగం చేసుకోడమే దేశానికి మనం చేసే సేవ అని చెప్పవచ్చు. దీనిని నీవు సమర్థిస్తావా? ఎందుకు?
జవాబు:
సహజ వనరులను సద్వినియోగం చేసుకోవటమే దేశానికి మనం చేసే సేవ అని చెప్పటాన్ని నేను సమర్థిస్తున్నాను.
- పెరుగుతున్న జనాభా వలన వనరుల వినియోగం విపరీతంగా పెరిగింది. ఈ పరిస్థితి కొంతకాలం కొనసాగితే, భవిష్యత్ తరాలకు వనరులు లభించవు.
- ప్రధానంగా శిలాజ వనరుల కొరత ఏర్పడుతుంది. పెట్రోలు, బొగ్గు నిల్వలు అడుగంటిపోతాయి. మనం సాధించిన అభివృద్ధి అంతా శక్తి పైన ఆధారపడి ఉంది.
- శక్తి రహిత ప్రపంచంలో ఏ పరిశ్రమలూ పనిచేయవు. ఏ రవాణా సాధనం నడవదు. అంటే మరలా మనం మధ్యయుగం నాటి పరిస్థితులకు వెళ్ళిపోతాము.
- ఇటువంటి విపత్కర పరిస్థితులు రాకుండా ఉండాలంటే వనరుల సద్వినియోగం ప్రతి పౌరుడు తన బాధ్యతగా భావించాలి.
- వనరుల వినియోగంలో విచక్షణ ఉపయోగింగ్ భాష్ తరాలకు వాటిని అందించాలి.
- తరిగిపోయే వనరులను తగ్గించి వాడటం అలవాటు చేసుకోవాలి.
- సౌరశక్తి, అలల శక్తి, పవనశక్తి వంటి ప్రత్యామ్నాయ వనరులకు ప్రాధాన్యం ఇవ్వాలి.
- వనరుల వినియోగంలో సాంకేతిక జ్ఞానం పెంచాలి. అప్పుడే భవిష్యత్ తరాలకు మనం శక్తిమయ ప్రపంచం అందించగలం. అదే మనం మన దేశానికి, రేపటి తరానికి చేసే సేవ.
ప్రశ్న 17.
జల వనరుల సౌలభ్యాన్ని బట్టి పంటల ఎంపిక, వ్యవసాయ విధానాలు ఉండాలి. ఈ విషయంలో రైతులకు అవగాహన కలిగించడానికి నినాదాలు తయారుచేయండి.
జవాబు:
వరి పంట వద్దు – ఆరు తడి పంటలు ముద్దు
నీటి వనరులు చూసుకో – సరైన పంటను ఎంచుకో
నీరు పుష్కలంగా లభిస్తే – వరి పంట సరే
వ్యవసాయం అంటే – వరి పంట ఒక్కటే కాదు
మైక్రో ఇరిగేషన్ వాడు – నీటిని ఆదాచేసి చూడు
బావి క్రింది సాగు అయితే – మెట్ట పంటలే మేలు
మంచాన్ని బట్టి కాళ్లు ముడుచుకోవాలి – నీటి లభ్యతను బట్టి పంటను మార్చుకోవాలి.
10th Class Biology 10th Lesson సహజ వనరులు Textbook InText Questions and Answers
10th Class Biology Textbook Page No. 228, 229
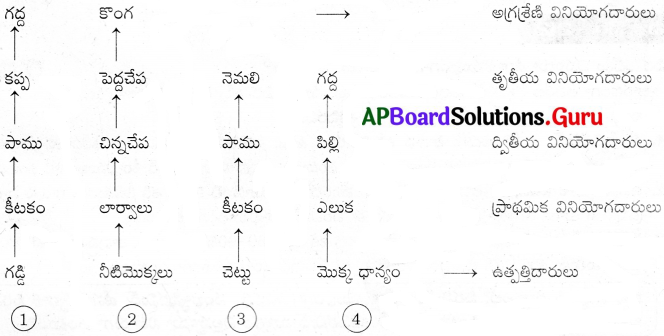
ప్రశ్న 1.

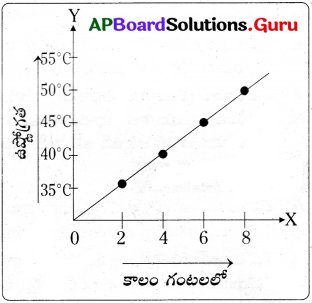
ఎ) గ్రామం – 1 లో ఎన్ని ఎకరాల భూమికి, నీటిపారుదల వసతి ఉంది?
జవాబు:
గ్రామం – 1 లో 947.75 ఎకరాలకు నీటిపారుదల వసతి ఉంది.
బి) గ్రామం – 1 లోని భూమి మొతానికి నీటిపారుదల వసతి కలిగించాలంటే ఎన్ని బావులు అవసరం?
జవాబు:
గ్రామం – 1 లోని భూమి మొత్తానికి నీటిపారుదల వసతి కల్పించాలంటే 620 బావులు అవసరం.
సి) గ్రామం – 1 లో బావుల సంఖ్య తక్కువగా ఉన్నప్పటికీ నీటిపారుదల వసతి గల భూ వైశాల్యం గ్రామం – 2 లో కన్నా ఎక్కువ. ఇది ఎలా సాధ్యం? నీటిపారుదల కలిగిన భూమి యొక్క వైశాల్యం పెరుగుతున్న జనాభాతో మారుతూ ఉంటుందా?
జవాబు:
గ్రామం – 1 లో బావుల సంఖ్య తక్కువగా ఉన్నప్పటికి వారు, సాగులో సూక్ష్మసేద్యం పాటించటం వలన ఎక్కువ భూమిని సాగుచేయగలిగారు. ఇంకుడు చెరువులు నిర్మించటం వలన బావులు ఎండిపోకుండా భూగర్భజలాన్ని కాపాడుకున్నారు. పెరుగుతున్న జనాభాకు తగినట్లు నీటిపారుదల కలిగిన భూమి వైశాల్యం పెరగదు. నీటి వనరుల లభ్యత ఆధారంగా నీటి పారుదల భూమి పెరుగుతుంది.
ప్రశ్న 2.
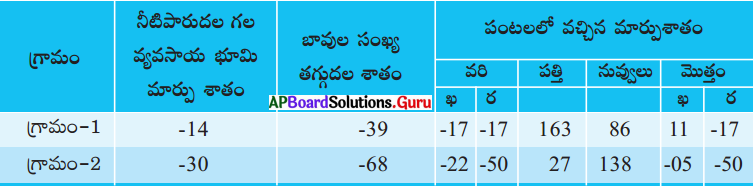
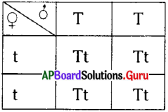
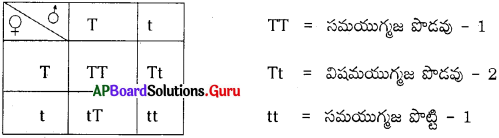
‘ఖ’ ఖరీఫ్ ను, ‘ర’ రబీపంటను సూచిస్తుంది.
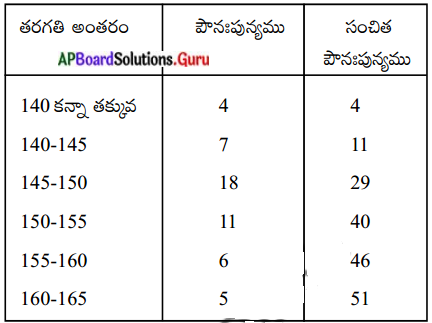
ఎ) ఇప్పటి బావుల సంఖ్య 155 అయితే, ఐదేళ్ళ క్రితం వాటి సంఖ్య ఎంత?
జవాబు:
ఐదేళ్ల క్రితం 194 బావులు ఉండేవి.
బి) ‘బావుల సంఖ్య తగ్గిపోవడం’ అనేది ఏం సూచిస్తుంది?
జవాబు:
బావుల సంఖ్య తగ్గటం భూగర్భజలాలు తరిగిపోవటంను సూచిస్తుంది.
సి) బావుల సంఖ్య తగ్గిపోవడం పంటలపై ఏవిధమైన ప్రభావం చూపుతుంది?
జవాబు:
బావుల సంఖ్య తగ్గటం వలన వ్యవసాయంలో నీటి కొరత ఏర్పడింది. వరి పంట సాగు బాగా తగ్గింది.
డి) రెండు పట్టికలను పోల్చంది. రెండు గ్రామాల్లో ఉన్న నీటిపారుదల వసతి గల భూ వైశాల్యం గురించి రెండు పట్టికలు ఏం చెప్తున్నాయో రాయండి.
జవాబు:
గ్రామం – 1 లో నీటి పారుదల కలిగిన భూవైశాల్యం 25% అయితే వడ్డిచెర్లలో ఇది 15% మాత్రమే. గ్రామం – 2లో 175 బావులు ఉన్నప్పటికి, 5 సంవత్సరాలలో వాటిలో 68% బావులు ఎండిపోయాయి.
ఇ) ఏ గ్రామం ఎక్కువగా ప్రభావితమైంది?
జవాబు:
రెండు గ్రామాలలో గ్రామం – 2 ఎక్కువగా బోరుబావులను కోల్పోయి వ్యవసాయ సమస్యలను ఎదుర్కొన్నది. ఖరీలో 22%, రబీలో 50% వరిసాగును కోల్పోయింది.
ఎఫ్) గ్రామాల్లో పండించే పంటల రకాలలో వచ్చిన మార్పు ఏమిటి?
జవాబు:
గ్రామాలలో నీటి కొరత వలన వధిసాగు పూర్తిగా తగ్గిపోయింది. దాని స్థానంలో రైతులు మెట్ట పంటలైన పత్తి, నువ్వులు వైపు మొగ్గు చూపారు.
జి) ఒకవేళ గ్రామం-1లో 45% బావులు ఎండిపోతే, బావుల సంఖ్య 39% తగ్గిపోతే, ఎంత శాతం బావులు గొట్టపుబావులుగా మార్చబడ్డాయి?
జవాబు:
16% బావులు గొట్టపు బావులుగా మార్చబడ్డాయి.
10th Class Biology Textbook Page No. 230
హెచ్) రెండు గ్రామాల వివరాలను పోల్చండి. ఏ గ్రామంలోని బావులు ఎక్కువ సంఖ్యలో ఎండిపోయాయి? మరో గ్రామంలో ఈ విధంగా జరగకపోవడానికి గల కారణమేమిటి?
జవాబు:
గ్రామం – 1తో పోల్చుకుంటే, గ్రామం – 2 లో బావులు ఎక్కువ సంఖ్యలో ఎండిపోయాయి. వారు సరైన భూగర్భజల నిర్వహణ చేయకపోవటం వలన బావులు ఎండిపోయాయి.
ఐ) తక్కువ భూమి గల సన్నకారు రైతులు, ఎక్కువ భూమి గల రైతులలో ఎవరి బావులు ఎండిపోవడం వలన ఎక్కువ ప్రభావితమైనారు?
జవాబు:
బావులు ఎండిపోవుట వలన అధికంగా సన్నకారు రైతులు నష్టపోయారు. వారికున్న కొద్ది పాటి భూమి నిరుపయోగం కావటం వలన తీవ్ర ఆర్థిక పరిస్థితులు ఎదుర్కొన్నారు.
జె) ఒకవేళ నీటివనరు తగ్గినా లేదా నీటి సదుపాయం లేకపోయినట్లయితే, అది నేల యొక్క స్వభావంపై ఎలాంటి ప్రభావం చూపుతుంది?
జవాబు:
నీటి సదుపాయం లేని భూములు ఎండిపోతాయి. ఈ ప్రాంతంలో మొక్కలు, గడ్డి మరణించి జీవజాలం తగ్గిపోతుంది. తీవ్ర ఎండల వలన ఈ ప్రాంతం ఎడారిగా మారిపోతుంది.
కె) ఎండిపోతున్న బావులు ఆ ప్రాంత ప్రజలపై ఏవిధమైన ప్రభావం చూపుతున్నాయి?
జవాబు:
ఎండిపోతున్న బావులు ఆ ప్రాంత ప్రజల ఆర్థిక వ్యవస్థను పూర్తిగా దెబ్బతీశాయి. చిన్నకారు రైతుల పంట భూములు నిర్వీర్యం అయినందున వారు వలస కూలీలుగా మారారు. మరికొందరు రైతులు వ్యవసాయం వదిలి ఇతర పనులలోనికి చేరారు. కొందరు పనికోసం పట్టణాలకు వలస వెళ్ళారు.
ఎల్) గ్రామం – 2 లో నీరు బాగా తగ్గిపోవడానికి గల కారణమేమిటి?
జవాబు:
గ్రామం – 2 రైతులకు భూగర్భ జల నిర్వహణపై అవగాహన లేదు. వారికి భూగర్భ జలం పెంచుకోవటం, ఇంకుడు చెరువులు నిర్మించటం, వర్షపు నీటిని ఆదా చేయటం వంటి పద్ధతులు తెలియవు. అందువలన గ్రామం – 2 ప్రాంతంలో నీటి వనరులు బాగా తగ్గిపోయాయి.
ప్రశ్న 3.
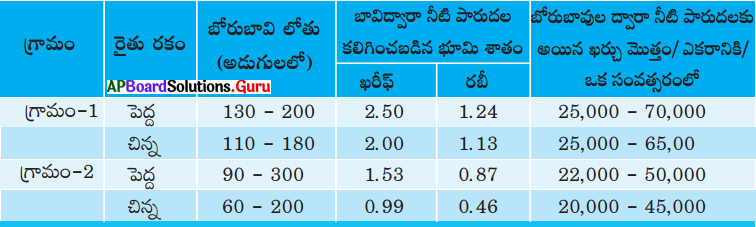
ఎ) చిన్న మరియు పెద్ద రైతులిద్దరికీ నీటి వనరు అందుబాటు ఒకే విధంగా ఉందా?
జవాబు:
లేదు, చిన్న రైతుల కంటే పెద్ద రైతులు అధిక నీటి వనరులు కలిగి ఉన్నారు. పెద్ద రైతుల బోరుబావులు ఎక్కువ లోతు కలిగి ఉండి అధిక నీటిని అందిస్తున్నాయి.
బి) ఒక ప్రాంతంలో ఉన్న ప్రతి వ్యక్తికి నీటి అందుబాటు ఒకేవిధంగా ఉండాలా?
జవాబు:
లేదు. ఒకే ప్రాంతంలో ఉన్న ప్రతి వ్యక్తికి నీటి అందుబాటు ఒకే విధంగా లేదు.
సి) రబీ కాలంలో కన్నా ఖరీఫ్ పంట కాలంలో ఒక బావి నుండి ఎక్కువ భూమికి నీటిపారుదల లభిస్తుంది. ఇది ఎలా సాధ్యపడుతుంది? దీనిని రైతు ఎలా వినియోగించుకోవాలి?
జవాబు:
ఖరీఫ్ పంట కాలంలో వర్షాలు కురుస్తాయి. అందువలన బావి నుండి ఎక్కువ భూమికి నీటిపారుదల లభిస్తుంది. అందువలన రైతులు ఖరీఫ్ కాలంలో ఎక్కువ భూమిని సాగుచేసుకోవాలి.
డి) ఒక బావి ద్వారా, 2.5% సాగుభూమికి నీటిపారుదల లభిస్తే, మొత్తం భూమికి నీరు అందాలంటే ఎన్ని బావులు అవసరం?
జవాబు:
సుమారుగా మొత్తం భూమికి నీరు అందాలంటే 40 బావులు అవసరమవుతాయి.
ఇ) బావుల సంఖ్య, బావి లోతు – ఈ రెండింటిలో ఏది ఖర్చుపై ఎక్కువ ప్రభావాన్ని చూపుతుంది?
జవాబు:
బావి లోతు పెంచటం కంటే కొత్త బావి తవ్వటం ఖర్చుతో కూడుకొన్న వ్యవహారం. అందుకే రైతులు బావిని తవ్వించేటప్పుడు ఎక్కువ లోతుకు ప్రాధాన్యం ఇస్తారు.
![]()
ఎఫ్) గ్రామం – 2 లో ఒక సన్నకారు రైతు సాగుభూమిపై ఖర్చు చేసే డబ్బు ఎంత? చిన్న రైతు ఈ డబ్బును ఏ విధంగా పొందుతాడు?
జవాబు:
గ్రామం – 2 లో సన్నకారు రైతు, సాగుభూమికి 20 వేల నుండి 45 వేల వరకు ఖర్చు చేస్తున్నాడు. రైతు ఈ పెట్టుబడి కోసం సాధారణంగా అప్పు చేస్తుంటాడు.
జి) సన్నకారు రైతు లేదా చిన్న రైతులు ఈ ఖర్చును తగ్గించుకోవాలంటే ఏ చర్యలు చేపట్టాలి? (ఉదా : నీటి ఎద్దడిని తట్టుకునే పంటలు పెంచడం)
జవాబు:
సన్నకారు రైతు ఖర్చు తగ్గించాలంటే, ఆరు తడి పంటలు పండించాలి. సూక్ష్మ సేద్యానికి ప్రాధాన్యత ఇవ్వాలి.
హెచ్) నీటి పారుదల వసతి గల భూ వైశాల్యాన్ని మొత్తం పెంచాలంటే బోరుబావి యొక్క లోతును పెంచడమే తగిన పరిష్కారమా? అవును లేదా కాదు లేదా ఎందుకు?
జవాబు:
లోతు పెంచినంత మాత్రాన నీటి వసతి పెరగదు. ఆ ప్రాంతంలో భూగర్భజలం పెంచే చర్యలు చేపట్టాలి. ఇంకుడు చెరువులు నిర్మించాలి. వర్షపు నీటిని ఆదాచేయాలి.
10th Class Biology Textbook Page No. 231
ప్రశ్న 4.
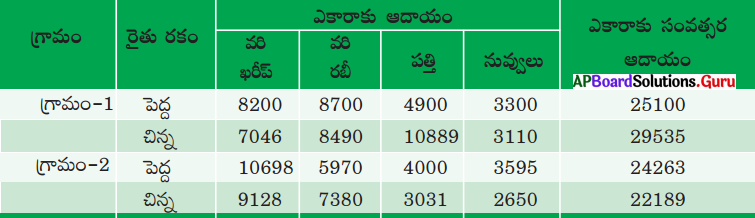
ఎ) గ్రామం-2 లో ఏ పంట చిన్నరైతుకు చాలా లాభదాయకంగా ఉంటుంది?
జవాబు:
గ్రామం – 2 లో వరిసాగు రైతుకు లాభదాయకంగా ఉంది.
బి) గ్రామం-1, గ్రామం-2 లలోని పెద్ద, చిన్నరైతుల మధ్య ఉన్న తేడా ఏమిటి?
జవాబు:
గ్రామం-1, గ్రామం-2 లలో చిన్న, పెద్ద రైతుల ఆదాయంలో వ్యత్యాసం ఉంది.
సి) గ్రామం-1 లో వరికి బదులు ఏ పంట చిన్నరైతుకు లాభదాయకంగా ఉంటుంది?
జవాబు:
గ్రామం-1 లో వరికి బదులు పత్తి లాభదాయకంగా ఉంటుంది.
డి) వరి నీటిని అత్యధికంగా వినియోగించుకునే పంట అయినప్పటికీ, రైతులు ఎందుకు వరినే పండించాలనుకుంటున్నారు?
జవాబు:
వరికి వచ్చే ఆదాయం అధికంగా ఉంటుంది. మార్కెట్లో వరికి డిమాండ్ ఉండుటవలన వరినే పండించాలనుకుంటున్నారు.
ఇ) తరిగిపోతున్న నీటి వనరు యొక్క ప్రభావం రైతులపై ఏ విధంగా ఉంది?
జవాబు:
నీటి వనరులు తరిగిపోవుట వలన రైతులు క్రమేణ మెట్టపంటలకు ప్రాధాన్యమిస్తున్నారు.
ఎఫ్) గ్రామం-2 లో నివసిస్తున్న చిన్న రైతు యొక్క ఆదాయం అతని ఖర్చుకు సరిపద ఉన్నదా?
జవాబు:
గ్రామం-2 లో చిన్న రైతు వ్యవసాయ ఖర్చు 20 వేల నుండి 45 వేల వరకు ఉంటే ఆదాయం కేవలం 22 వేలు మాత్రమే ఉంది. కావున రైతు నష్టపోతున్నాడు.
జి) గ్రామం-2 లో చిన్న రైతుల యొక్క దయనీయమైన పరిస్థితులకు ఇతర ప్రధాన కారణాలేమైనా ఉన్నాయా?
జవాబు:
గ్రామం-2 లో రైతు దయనీయ పరిస్థితికి, నీటి కొరతతో పాటు, వ్యవసాయ పరిజ్ఞానం లేకపోవటం, ఋతుపవనాలు సక్రమంగా లేకుండుట వంటి ఇతర కారణాలు ఉన్నాయి.
హెచ్) గ్రామం-2 లో చిన్న రైతుకు వ్యవసాయం ఒక వృత్తిగా, లాభదాయకంగా ఉంటుందని అనుకుంటున్నారా?
జవాబు:
గ్రామం-2 లో చిన్నరైతుకు వ్యవసాయం లాభసాటి వృత్తికాదు.
![]()
ఐ) తన అవసరాలు తీర్చుకోవడానికి రైతు ఇతర వృత్తులను ఎంచుకోవాలా?
జవాబు:
వ్యవసాయంతో పాటు, పాడిపరిశ్రమ, వర్మీ కంపోస్ట్ వంటి వ్యవసాయ ఆధారిత వృత్తులు ఎంచుకోవటం మంచిది.
జె) గ్రామం-2 లో నీటి వసతి చిన్న రైతుపై ఏ విధమైన ప్రభావం చూపిస్తుంది?
జవాబు:
నీటి వసతి సరిగా లేక చిన్నరైతు నష్టాలు చూస్తున్నాడు. అందువలన చిన్న రైతులు ఆర్థికపరమైన ఇబ్బందులకు గురికావలసి వస్తున్నది.
10th Class Biology Textbook Page No. 232
ప్రశ్న 5.
ఎ) బావులలోకి నీరు చేరేలా చేయడం ఎలా?
జవాబు:
ఇంకుడు చెరువులు, వర్షపు నీటిని భూమిలోనికి ఇంకింపచేయటం ద్వారా బావులలోనికి నీరు చేర్చవచ్చు.
బి) గ్రామం-2 లో ఎండిన బావులలోకి నీరు చేరేలా చేసినట్లయితే రైతుకు ఏ విధంగా సహాయపడుతుంది?
జవాబు:
గ్రామం-2 లో ఎండిన బావులలోనికి నీరు చేరినట్లయితే రైతులకు నీటి వసతి కలిగి పంటలు పండిస్తారు. అందువలన వారి ఆర్ధిక పరిస్థితి మెరుగుపడుతుంది.
సి) పైన ఉదహరించిన అధ్యయనం, నీటి వనరు మరియు రైతులపై దాని యొక్క ప్రభావం గురించి ఏం చెబుతుంది?
జవాబు:
రైతు ఆర్థిక స్థితిగతులు నీటి వనరు లభ్యతపై ఆధారపడి ఉంటుందని అర్థమైంది.
డి) నీటిని విచక్షణతో ఎలా వినియోగించవచ్చని అనుకుంటున్నావు?
జవాబు:
నీటిని విచక్షణతో వినియోగిస్తే దాదాపు 25% నీరు ఆదాచేయవచ్చు. నీటి వృథాను అరికట్టడమే, నీటి విచక్షణా వినియోగం అవుతుంది.
ఇ) గ్రామం-2 లో కన్నా గ్రామం-1 లో రైతుల పరిస్థితి బాగుండదానికి కారణమేమిటి?
జవాబు:
గ్రామం-2 లో రైతులు భూగర్భజల వినియోగంపై అవగాహన పెంపొందించుకొన్నారు. భూగర్భ జలాలను పెంచుకొన్నారు. కావున వారి పరిస్థితి మెరుగుగా ఉంది.
ఎఫ్) గ్రామం-2, గ్రామం-1 లలో రైతులు భూగర్భ జలవనరులను ఏ విధంగా సంరక్షించుకుంటున్నారు?
జవాబు:
ఇంకుడు గుంటలు నిర్మించటం, చెక్ డ్యామ్ లు కట్టటం, ఇంకుడు చెరువులను నిర్మించటం, వర్షపు నీటిని సంరక్షించటం వంటి పద్ధతుల ద్వారా రైతులు భూగర్భ జలవనరులను సంరక్షించుకుంటున్నారు.
10th Class Biology Textbook Page No. 233
ప్రశ్న 6.
ICRISAT అంటే ఏమిటి? ఎక్కడ ఉంది? అది నిర్వహించే కార్యక్రమాలపై మీ ఉపాధ్యాయునితో చర్చించి నివేదిక తయారుచేయండి.
జవాబు:
‘ఇంటర్నేషనల్ క్రాప్ రీసెర్చి ఇనిస్టిట్యూట్ ఫర్ సెమి-ఎరిడ్ ట్రాపిక్స్’ను సంక్షిప్తంగా ఇక్రిసాట్ అంటారు. ఇది హైదరాబాద్లో ఉంది. భారతదేశం వంటి ఉష్ణ మండల ప్రాంతాలలో పండే పంటల పైన వీరు పరిశోధన చేస్తుంటారు. వరి వంగడ వృద్ధి, చెరకు, పత్తి పంటల దిగుబడులు పెంచటం, రైతుల ఆర్థిక స్థితి మెరుగుపర్చటం కోసం వీరు కృషి చేస్తుంటారు. వీరి సేవల వలన వ్యవసాయంలో ఆధునిక వంగడాలు, ఆధునిక సేద్య పద్ధతులు అందుబాటులోనికి వచ్చాయి.
ఇంటర్నేషనల్ క్రాప్ రీసెర్చ్ ఇన్స్టిట్యూట్ ఫర్ సెమి-ఎండ్ ట్రాపిక్స్ (ICRISAT) గ్రామస్తులను పెద్ద సంఖ్యలో విద్యా వంతులను చేయడమే కాకుండా, సరైన ధరతో నీటి నిలువ మరియు నేల సంరక్షణా నిర్మాణాలు చేపట్టడానికి కావలసిన సాంకేతికతను అందించారు. ఈ పద్దతులన్నీ సామాజికంగా, వ్యక్తిగతంగా రైతుపై కేంద్రీకరింపబడ్డాయి. కొన్ని వనరులను తిరిగి పొందడానికి, కొన్నింటిని తరిగిపోకుండా సంరక్షించుకోవడానికి ఈ పద్దతులు సహకరించాయి. కావున సుస్థిర యాజమాన్యం చేపట్టడం జరిగింది.
10th Class Biology Textbook Page No. 235
ప్రశ్న 7.
ఎ) కొత్తపల్లి కేస్టడీలో సహజ వనరులను సద్వినియోగం చేసుకోవడంలో వారు అనుసరించిన మార్గాలు ఏమిటి?
జవాబు:
కొత్తపల్లి కేస్టడీలో సహజవనరుల సంరక్షణకు –
- ఇంకుడు చెరువులు నిర్మించారు.
- బంజరు భూములలో మొక్కలు పెంచారు.
- గట్లమీద గైరిసీడియం మొక్కలు నాటారు.
- బోరుబావుల సంరక్షణ చేపట్టారు.
- నీటి పొదుపునకు సూక్ష్మ నీటిపారుదల పద్ధతులు అవలంభించారు.
- వెడల్పు పద్ధతి అవలంబించి నేల, నీటిని సంరక్షించారు.
బి) ఈ కేస్టడీలో నీటిని పొదుపు చేయడానికి ఏ ఏ పద్ధతులను అనుసరించినట్లుగా మీరు గుర్తించారు?
జవాబు:
ఈ కేస్టడీ ద్వారా నీటిని పొదుపు చేయటానికి ఈ క్రింది పద్దతులు తోడ్పడతాయి.
- రాళ్లు, మట్టి, కంకరతో నీటి ప్రవాహానికి గట్టు కట్టి ఇంకుడు చెరువులు నిర్మించటం.
- వర్షపు నీటిని నిల్వ చేసి భూమిలోకి మళ్ళించటం.
- ఏటవాలు ప్రాంతాలలో కాంటూర్ పట్టి పంటలు పండించుట.
- ఇంకుడు గుంటలు ఏర్పాటు చేసి దానిలోనికి వర్షపు నీటిని మళ్ళించటం.
- డ్రిప్ ఇరిగేషన్ స్ప్రింక్లర్ల ద్వారా సూక్ష్మ నీటి పారుదల పద్ధతులు పాటించటం.
- బోరుబావుల సంరక్షణ.
- పర్వత వాలు ప్రాంతాలలో చెక్ డ్యాములు నిర్మించటం.
- వాటర్షెడ్ పథకాలు అమలుచేయటం వంటి పద్ధతులు పాటించి నీటిని పొదుపు చేయవచ్చు.
ప్రశ్న 8.
ఎ) నీటి వనరుల పట్ల జాగ్రత్త వహించకుంటే ఏం జరుగుతుందనుకుంటున్నావు?
జవాబు:
‘నీటి వనరుల పట్ల జాగ్రత్త వహించకపోతే, మనం నీటి కొరతను ఎదుర్కొనవలసి వస్తుంది. తద్వారా పంటలు పండించలేము. ఇది ఆహార కొరతకు దారితీస్తుంది.
బి) భవిష్యత్తులో మన అవసరాలు ఏ విధంగా తీర్చుకోగలమనుకుంటున్నారు?
జవాబు:
సహజ వనరుల వినియోగం పట్ల ప్రజలలో అవగాహన పెంచి, వాటిని సక్రమంగా వినియోగించుకొనేలా జాగ్రత్తపడాలి. తరగని వనరుల వినియోగంపై దృష్టి పెట్టాలి. తరిగే వనరులకు ప్రత్యామ్నాయ వనరులు వెతకాలి.
సి) ఇతర రాష్ట్రాలు లేదా అవసరమైతే ఇతర దేశాలపై మనం ఆధారపడవలసి వస్తుందనుకుంటున్నారా?
జవాబు:
నీటి వినియోగంపై నిర్లక్ష్యంగా వ్యవహరిస్తే రాబోయే రోజులలో మనం నీటి కొరకు ఇతర రాష్ట్రాలు, దేశాలపై ఆధారపడవలసి వస్తుంది.
డి) నీటిని పొదుపుగా వాడటానికి, సాగు విధానానికి ఎలాంటి సంబంధం ఉంది?
జవాబు:
నీటిని పొదుపుగా వాడటం ద్వారా పంట విస్తీర్ణాన్ని పెంచుకోవచ్చు. కరవు పరిస్థితులలో కూడా పంటలను సాగు చేసుకోవచ్చు. అధిక పంటలు పండించవచ్చు.
ఇ) ఆంధ్రప్రదేశ్ లో వ్యవసాయంలో నీటిపారుదల కోసం, వాడే నీటిని తగ్గించడం సాధ్యమా? అది ఏవిధంగా సాధ్యపడుతుంది?
జవాబు:
ఆంధ్రప్రదేశ్ లో వ్యవసాయంలో నీటిపారుదల కోసం వాడే నీటిని తగ్గించటం సాధ్యమే. మన రాష్ట్రంలో వరి ప్రధాన పంటగా ఉంది. దీనికి నీరు కావాలి. దీని స్థానంలో ఆరు తడి, మెట్ట పంటలకు ప్రాధాన్యమివ్వాలి.
ఎ) వరిలో ఆధునిక వ్యవసాయ పద్ధతులు, ‘శ్రీవరి’ వంటి పద్ధతులు పాటించాలి.
బి) వరిని తక్కువ నీటితో మెట్టపంటగా కూడా పండించవచ్చు.
సి) ఇతర పంటలలో స్ప్రింక్లర్లు, డ్రిప్ వంటి వాటితో నీటి వనరులను సంరక్షించవచ్చు.
ఎఫ్) నీటి విస్తరణ, వినియోగానికి చట్టాలు అవసరమా? అయితే ఎందుకు?
జవాబు:
నీటి విస్తరణ, వినియోగానికి చట్టాలు అవసరము. అప్పుడే నీటిని జాగ్రత్తగా, పొదుపుగా వాడతారు. లేనిచో ఈ సహజవనరు దుర్వినియోగం అవుతుంది.
![]()
ప్రశ్న 9.
ఎంత శాతం భూవైశాల్యం ఇతర నీటి వనరుల వలన నీటిపారుదల సదుపాయం పొందింది?
జవాబు:
ఇతర వనరుల ద్వారా 5% భూవైశాల్యం నీటిపారుదల సౌకర్యం కలిగి ఉంది.
10th Class Biology Textbook Page No. 236
ప్రశ్న 10.
మన రాష్ట్రానికి ఈ నదులు ఎంతవరకు లాభదాయకంగా ఉండాలో అంతమేరకు ఉపయోగపడటం లేదు. దీనికి గల కారణం ఏమిటి?
జవాబు:

మన రాష్ట్రంలో నదులు, కాలువల ద్వారా 37% భూమి సాగులోనికి వచ్చింది. చెరువుల వలన 15% భూమి సాగుచేయబడుతుంది. నదీజలాలను మనం పూర్తిగా వినియోగించుకోలేకపోతున్నాము. చాలా నదీ జలాలు సముద్రంలో కలిసిపోతున్నాయి.
భూవిస్తీర్ణంలో చాలా భాగం నదీ పరీవాహక ప్రాంతాల కంటే ఎత్తులో ఉండుట వలన నదీ జలాలు అందటం లేదు. నదీ జలాల అనుసంధానం లేకపోవుట కూడా ఈ పరిస్థితికి ఒక కారణం.
ప్రశ్న 11.
భూగర్భ జలాలను పెంచుకోవాల్సిన అవసరం ఏమిటి?
జవాబు:
వ్యవసాయ నీటివనరులో భూగర్భ జలాల వాటా 43% ఉంది. ఈ భూగర్భ జలాన్ని సంరక్షించుకుంటే వ్యవసాయరంగం తీవ్ర నీటి ఎద్దడిని ఎదుర్కొనవలసి ఉంటుంది. మనమందరం త్రాగు నీటి కోసం భూగర్భజలాలపై ఆధారపడుతున్నాము. భూగర్భజలాలు లేకుంటే త్రాగునీటి కొరత ఏర్పడి జీవనం స్తంభించిపోతుంది.
ప్రశ్న 12.
భూగర్భజల వనరులు వేగంగా తరిగిపోతున్నాయి కదా! దీనికి ప్రత్యామ్నాయాలు ఏమిటి?
జవాబు:
ఋతుపవనాల రాకడతో మార్పులు సంభవించటం వలన భూగర్భజలాల వినియోగంపై ఒత్తిడి పెరిగింది. డ్రిల్లింగ్, లోతైన గొట్టపుబావులు, బోరుబావులను తవ్వడం వంటి చర్యల వలన, విచక్షణారహితంగా భూగర్భజలాన్ని వాడటం వలన, భూగర్భజలాలు తరిగిపోతున్నాయి.
ప్రత్యామ్నాయాలు :
- వర్షపు నీటిని భూమిలోనికి ఇంకింపచేయటం
- ఇంకుడు గుంటలు నిర్మించటం
- ఇంకుడు చెరువులు ఏర్పాటు చేయటం
- అడవుల పెంపకం వంటి చర్యల ద్వారా భూగర్భజలాన్ని పెంచవచ్చు.
ప్రశ్న 13.
గోదావరి నదీజలాలు మన రాష్ట్రంలోని ప్రాజెక్టులను నింపడానికి సరిపోడంలేదు. పైనున్న రాష్ట్రాలు పరిమితులకు మించి నీటిని వినియోగిస్తుండడమే దీనికి ప్రధాన కారణం. ఈ విషయాలలో దేశాలు, రాష్ట్రాలు అందరికీ న్యాయం కలిగేలంటే ఏం చేయాలి?
* సరిపడా నీటిపారుదల సౌకర్యం కలిగించాలంటే రాష్ట్రాలు, దేశాలు ఏ విధంగా పనిచేయాలి?
జవాబు:
- జల వనరుల పంపిణీకి జాతీయ స్థాయిలో కమిటీ ఏర్పాటు చేయాలి.
- నీటి పంపిణీ యాజమాన్యం కేంద్రం అధీనంలో ఉంటాయి.
- జల పంపిణీ వివాదాల పరిష్కారానికి ప్రత్యేక ట్రిబ్యునల్ ఉండాలి.
- జనాభా ప్రాతిపదికన జల పంపిణీ జరగాలి.
- ఆనకట్టల నిర్మాణానికి, ఎత్తు పెంపుదలకు, కేంద్ర జల కమిటీ అనుమతిని తప్పనిసరి చేయాలి.
- జలాలపై ఆధారపడిన భూవిస్తీర్ణం ఆధారంగా నీటి వనరుల పంపిణీ జరగాలి.
10th Class Biology Textbook Page No. 237
ప్రశ్న 14.
నీరు తప్ప మీ పరిసరాలలోని ఏదైనా ఒక ముఖ్య వనరును గురించి రాయండి.
జవాబు:
గాలి, నీరు, నేల వలె పర్వతాలు, కొండలు కూడా ముఖ్యమైన సహజవనరులు. మా ప్రాంతంలో చిన్న కొండలు విస్తరించి ఉన్నాయి. వీటిని ప్రభుత్వం నుండి లీజుకు తీసుకొని రాళ్ల కొరకు పగలగొడుతున్నారు. దీనివలన మా పరిసర ప్రాంతాలలో క్రషింగ్ యూనిట్లు విస్తరించాయి. ఇక్కడ కొండ రాళ్ళను పగలగొట్టి, కంకర, చిప్స్, డస్టగా మార్చుతున్నారు. నష్టాలు : దీనివలన సహజ వనరులైన కొండలు అంతరించిపోతున్నాయి. కొండలు పేల్చడానికి ప్రేలుడు పదార్థాలు వాడటం వలన శబ్ద కాలుష్యం జరుగుతుంది. క్రషింగ్ యూనిట్ వలన పరిసరాలంతా దుమ్ము పేరుకుపోయింది. చెట్లపై ఈ రాతి దుమ్ము పేరుకుపోవటం వలన కిరణజన్యసంయోగక్రియ రేటు తగ్గి మొక్కలు మరణిస్తున్నాయి. పరిసరాలలోని జనాభా శ్వాస సంబంధ వ్యాధులతో బాధపడుతున్నారు.
పరిష్కారాలు :
- క్రషింగ్ యూనిట్ చుట్టూ ఎత్తైన ప్రహరీలు ఏర్పర్చాలి.
- పచ్చదనం కోసం మొక్కలను అధికంగా పెంచాలి.
- కొండలను సహజ వనరులుగా గుర్తించి పరిరక్షణ చర్యలు చేపట్టాలి.
10th Class Biology Textbook Page No. 238
ప్రశ్న 15.
మీ పరిసరాలలోని ఒక ప్రధాన వనరును వాడుతూ, సంరక్షించుకునే విధంగా ఇతరులను ఎలా సంసిద్ధులను
జవాబు:
మాది వ్యవసాయ ఆధారిత ప్రాంతం. ఇక్కడ ప్రధాన వనరు నేల. నేల సంరక్షణ గురించి, నేల యాజమాన్య పద్ధతుల గురించి రైతులకు తెలియజేస్తాను.
- రసాయనిక ఎరువుల స్థానంలో జీవ ఎరువులకు ప్రాధాన్యమివ్వాలని వివరిస్తాను.
- పంట మార్పిడి పద్ధతి ఆవశ్యకతను తెలియజేస్తాను. 3. రక్షక పంటల ప్రయోజనాన్ని వివరిస్తాను.
- వర్మీ కంపోస్ట్, పచ్చిరొట్ట ఎరువుల తయారీ, వాటి ప్రయోజనాలు తెలియజేస్తాను.
- నత్రజని పంటల అవసరం, వాటి ప్రాధాన్యం తెలుపుతాను.
- ఆరు తడి పంటల ప్రయోజనం తెలిపి, రైతులను సంసిద్ధులను చేస్తాను.
![]()
ప్రశ్న 16.
సుస్థిర యాజమాన్యానికి కొత్తపల్లి గ్రామస్తులు ఏం చేశారు?
జవాబు:
సుస్థిర యాజమాన్యానికి కొత్తపల్లి గ్రామస్థులు క్రింది చర్యలు చేపట్టారు.
- నేల, నీటి సంరక్షణ కార్యక్రమాలు చేపట్టారు.
- వెడల్పు, చాళ్లు తీయటం, తక్కువ ఎత్తు పెరిగే పంటలు పండించటం, కాంటూర్ సేద్యం వంటి నేల యాజమాన్య పద్ధతులు పాటించారు.
- సూక్ష్మ సేద్య పద్ధతులలో డ్రిప్ ఇరిగేషన్ స్ప్రింక్లర్లు వాడి నీటిని ఆదా చేశారు.
- వరి, చెరకు పంటల స్థానంలో ఆరు తడి పంటలకు ప్రాధాన్యం ఇచ్చారు.
- గట్లు స్థిరంగా ఉండటానికి, నేలలో పోషకాలు పెంచటానికి గట్ల వెంబడి గెరిసీడియం మొక్కలు పెంచారు.
- రోడ్ల వెంబడి, పొలాలగట్ల వెంబడి ఉపయోగకర మొక్కల జాతులను పెంచి బీడు భూములను అభివృద్ధి చేశారు
10th Class Biology Textbook Page No. 240
ప్రశ్న 17.
మీ పరిసర ప్రాంతాలలోని ఒక ‘లాన్’ ను పరిశీలించండి. దానిని కాపాడుకోవటానికి ఎలాంటి యాజమాన్య పద్ధతులు పాటిస్తున్నారు?
జవాబు:
లాన్ సంరక్షణకు ఈ క్రింది చర్యలు తీసుకుంటాను.
- లాను ప్రతిరోజు సాయంత్రం నీటి సరఫరా చేయాలి.
- గుబురుగా పెరిగే ప్రాంతాలను కత్తిరించాలి.
- కొంత ఎత్తున పెరిగిన తరువాత సమంగా కత్తిరించాలి.
- లాలోని కలుపు మొక్కలను నిర్మూలించాలి.
- లాక్కు పోషకాలు అందిస్తూ ఉండాలి.
ప్రశ్న 18.
లాన్ నుండి తొలగించే వివిధ మొక్కల పేర్లను తోటమాలి నుండి కనుక్కోండి. రైతు కూడా పొలంలో ఇదే విధానాన్ని పాటిస్తాడా? లాస్ జీవవైవిధ్యాన్ని ప్రోత్సహిస్తుందా?
జవాబు:
లాలో తుంగ వంటి కలుపు మొక్కలు ఉన్నాయి. వీటిని సాధారణంగా చేతితో పీకి వేస్తుంటారు. పొలంతో రైతులు కూడ ఇదే పద్ధతిని అవలంభిస్తుంటారు. లాలో ఒకేరకమైన గడ్డిజాతి పెరుగుతూ ఉంటుంది. కావున ఇది జీవవైవిధ్యాన్ని ప్రోత్సహించదు.
10th Class Biology Textbook Page No. 241
ప్రశ్న 19.
శిలాజ ఇంధనాలు మనకు ఏ విధంగా ఉపయోగపడతాయి?
జవాబు:
బొగ్గు, పెట్రోలు, సహజ వాయువులను “శిలాజ ఇంధనాలు” అంటారు. మనం ఉపయోగిస్తున్న శక్తి వనరులలో ప్రధానమైనవి శిలాజ ఇంధనాలే. పరిశ్రమలలో, వాహనాలలో, విద్యుత్ తయారీకి వీటిని విరివిగా వాడుతున్నాము.
పెట్రోలు వాహనాలలోనే కాకుండా ప్లాస్టిక్, సింథటిక్, రబ్బరు, నైలాన్, మందులు, సౌందర్య పదార్థాలు, మైనం, పరిశుభ్రత ఉత్పత్తులు, వైద్య పరికరాలు మొదలైనవి తయారు చేయడంలోనూ ఉపయోగిస్తారు.
ఎ) వాటిని ఎందుకు సంరక్షించుకోవాలి?
జవాబు:
శిలాజ ఇంధనాలు తరిగిపోయే వనరులు. వీటి నిల్వలు ఉపయోగిస్తున్న కొలదీ తరగిపోతాయి. తిరిగి వీటి ఉత్పత్తికి లక్షల సంవత్సరాలు పడతాయి. కావున ఈ వనరుల వినియోగంలో విచక్షణ అవసరం.
10th Class Biology Textbook Page No. 242
ప్రశ్న 20.
సౌర, పవన, జల, అలల విద్యుదుత్పత్తి గురించిన సమాచారాన్ని సేకరించండి. స్క్రిప్ పుస్తకం తయారుచేయండి.
జవాబు:

సౌరశక్తి :
తరగని శక్తి వనరులలో సౌరశక్తి ఒకటి. సోలార్ ప్యానల్స్ ఉపయోగించి సౌరశక్తి నుండి విద్యుత్ తయారుచేస్తారు. దీనిని బ్యాటరీలలో నిల్వ చేసివాడవచ్చు. సోలార్ హీటర్లు, సోలార్ కుక్కర్లు, సోలార్ లైట్లు ఇప్పటికే ప్రజాదరణ పొందాయి. భవిష్యత్ కాలంలో సౌరశక్తి వినియోగం కొరకు, సోలార్ ఇళ్లు, సోలార్ వాహనాల కొరకు ప్రయోగాలు చేస్తున్నారు. ఇది కాలుష్యరహితం మరియు అనంతం.

పవనశక్తి :
ఎత్తైన ప్రదేశాలలో పర్వత స్నాయువులపైన గాలివేగం ఎక్కువగా ఉంది. ఈ పవనశక్తితో ఫ్యాన్లు తిప్పి తద్వారా, దానికి అమర్చిన టర్బైన్ తిప్పుతారు. అందువలన విద్యుత్ ఉత్పత్తి జరుగుతుంది. ఇది తరగని వనరు. పరిసరాలు కలుషితం కాదు. అయితే అన్ని ప్రదేశాలకు ఇది అనుకూలంగా ఉండదు.
జలవిద్యుత్ :
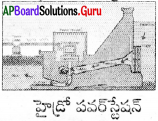
విద్యుత్ ఉత్పత్తిలో జలవిద్యుత్ ది అగ్రస్థానం. నదులు, కాలువలపై ఆనకట్టలు పవన విద్యుత్ నిర్మించి నీటి మట్టం ఎత్తు పెంచుతారు. అందువలన నీటికి స్థితిశక్తి లభిస్తుంది. ఎత్తైన ప్రదేశం నుండి నీటిని క్రింద ఉన్న టర్బైన్స్ మీదకు పంపటం వలన టర్బైన్ తిరిగి విద్యుత్ ఉత్పత్తి జరుగుతుంది. ఇది తరగని వనరు. పర్యావరణ హితం. కావున ఈ ప్రక్రియ ప్రాధాన్యతను సంతరించుకుంది.

అలల విద్యుత్ :
సముద్రం తీర ప్రాంతంలో అలలను ఉత్పత్తి చేస్తుంది. ఈ అలలు గతిశక్తి కలిగి ఉంటాయి. అలల గతిశక్తి ఆధారంగా టర్బెన్స్ తిప్పి విద్యుత్ తయారుచేస్తారు. ఇది తరగని వనరు. పర్యావరణ హితం. తీర ప్రాంతాలలో కూడా ఇది బాగా అనుకూలం.
ఇటువంటి తరగని వనరులను వినియోగించుకోవటం వలన ఇంధన కొరతను, శక్తి సంకటాన్ని సమర్థవంతంగా అధిగమించవచ్చు.
ప్రశ్న 21.
అణువిద్యుత్ ప్రభావాల గురించి మీ ఉపాధ్యాయునితో చర్చించండి.
జవాబు:
అణువిద్యుత్ తయారీకి రేడియో ధార్మిక పదార్థాలైన యురేనియం, థోరియం వంటి భారలోహాలు ఉపయోగిస్తారు. వీటిని మండించి ఉత్పత్తి అయిన ఉష్ణంతో నీటిని ఆవిరిగా మార్చి టర్బైన్ తిప్పటం వలన విద్యుత్ ఉత్పత్తి జరుగుతుంది. ఈ ప్రదేశాలను అణు విద్యుత్ కేంద్రాలు అంటారు.
మన దేశంలో తారాపూర్ (మహారాష్ట్ర), కల్పకం (తమిళనాడు), Kaiga (కర్ణాటక), Kakrapar (గుజరాత్), Narora (ఉత్తరప్రదేశ్), Rawatbhata (కోట) రాజస్థాన్) Kudenkulam (తమిళనాడు) లో అణు విద్యుత్ కేంద్రాలు ఉన్నాయి.
దీని వినియోగంలో ఉన్న సమస్యలు :
- అణువిద్యుత్ కేంద్రాల ఏర్పాటు బాగా ఖర్చుతో కూడుకొన్న వ్యవహారం.
- రేడియో యాక్టివిటీ పదార్థాలు నీటిని చేరి జలకాలుష్యం కలిగిస్తాయి.
- రేడియో యాక్టివిటీ పదార్థాలకు, వాటి గనులకు రక్షణ సమస్య ఉంది.
- అణు విద్యుత్ కేంద్రాల నుండి వచ్చే లీకేజీలు ప్రమాదకర స్థితిని కలిగిస్తాయి.
- కార్బన్ ఉత్పత్తిని తగ్గించదు. అందువలన కాలుష్యం జరుగుతుంది. (థర్మల్ విద్యుత్ కేంద్రం వలె)
![]()
ప్రశ్న 22.
ఉత్తరాఖండ్ వంటి ప్రకృతి ప్రళయాలకు కారణాలు ఆలోచించండి.
జవాబు:
ఉత్తరాఖండ్ వంటి ప్రకృతి ప్రళయాలకు కారణాలు :
- సరైన నీటి పారుదల యాజమాన్యం లేకపోవడం.
- కొండల సంరక్షణ లేకపోవడం వలన చరియలు విరిగిపడిపోయాయి.
- కొండ చరియలు వరద ప్రవాహ దిశను మార్చి ఉధృతిని పెంచాయి.
- కొండ ప్రాంతాలలో చెట్లు నరకటం వలన క్రమక్షయం జరిగింది.
- చాలా పల్లపు ప్రాంతాలు ఆక్రమణలకు గురై పూడ్చివేయటం జరిగింది.
- ప్రకృతి మార్పుల వలన విపరీతమైన వర్షాలు కురవడం.
- వరద నీటిని సంరక్షించే, నియంత్రించే నిర్మాణాలు లేకపోవటం.
- కొండ ప్రాంతాలలో నీటి నియంత్రణ ఏర్పాట్లు లేకపోవటం.
10th Class Biology Textbook Page No. 243
ప్రశ్న 23.
ఏ ఏ వనరుల వినియోగాన్ని తగ్గించవచ్చు?
జవాబు:
నేల, విద్యుత్, పెట్రోలు, డీజిల్, బొగ్గు వంటి వనరుల వినియోగాన్ని తగ్గించవచ్చు. వీటి స్థానంలో ప్రత్యామ్నాయ వనరులు వాడి సహజ వనరులను సంరక్షించవచ్చు.
ప్రశ్న 24.
మన వనరులను సంరక్షించుకోవడానికి తిరిగి ఏ ఏ వస్తువులను వినియోగించవచ్చును?
జవాబు:
- ప్లాస్టిక్ కవర్ల బదులుగా గుడ్డ సంచులు వాడి పర్యావరణాన్ని కాపాడవచ్చు.
- కాగితం తయారీకి చెట్లను నరకకుండా రీసైక్లింగ్ కాగితం వాడవచ్చు.
- ఇనుమును ఖనిజం నుండి తయారుచేయకుండా వాడిన ఇనుమును పునఃచక్రీయం చేయవచ్చు.
- చాలా వ్యర్థాలను తిరిగి వాడుకొనే అవకాశం ఉంది. దీని వలన వనరులను సంరక్షించవచ్చు.
ప్రశ్న 25.
పండుగలు, ఉత్సవాల సందర్భాలలో పెద్ద ఎత్తున విద్యుత్ అలంకరణలు అవసరమని నీవు భావిస్తున్నావా?
జవాబు:
పండుగలు, ఉత్సవాల సందర్భాలలో పెద్ద ఎత్తున విద్యుత్ అలంకరణలు అవసరం లేదు. దీనివలన లక్షల కొద్ది డబ్బు వృధా కావటమే గాక, విద్యుత్ ఇంధన వనరులు దుర్వినియోగం అవుతాయి. కావున వీటిని చేపట్టకుండా ఉండటం మంచిది.
ప్రశ్న 26.
ఇంట్లోని చెత్తను పారవేసే ముందు వ్యర్థాలను ఎందుకు వేరు చేయాలి?
జవాబు:
ఇంట్లోని చెత్తను పారవేసేముందు వాటిని తడి, పొడి చెత్తలుగా వేరుచేయాలి. తడిచెత్త భూమిలో కుళ్ళిపోతుంది కావున వీటిని ఎరువుల తయారీకి వాడవచ్చు. పొడి చెత్తను విభజించి వాటిని పునఃచక్రీయం చేయవచ్చు. చెత్తను పారవేసే ముందు వేరుచేయకపోతే వాటి వినియోగం సాధ్యం కాదు.
ప్రశ్న 27.
చెత్తబుట్టలో వ్యర్థాలను పారవేయడానికి ప్లాస్టిక్ సంచిని పెట్టడం మంచిదేనా?
జవాబు:
చెత్తబుట్టలో వ్యర్థాలను పారేయటానికి ప్లాస్టిక్ సంచిని వాడటం మంచిది కాదు. ప్లాస్టిక్ సంచుల వినియోగం పెరిగి పర్యావరణం కలుషితం జరుగుతుంది. ప్లాస్టిక్ వ్యర్థాలు భూమిలో కలిసిపోవటానికి లక్షల సంవత్సరాలు పడతాయి. కావున వీటి వినియోగాన్ని నిలిపివేయాలి.
ప్రశ్న 28.
పర్యావరణానికి కలిగే హానిని తొలగించటానికి ‘ఏర్పరచడం’ తిరిగి ఏయే కార్యక్రమాల ద్వారా సాధ్యమవుతుందో చర్చించండి.
జవాబు:
- వనమహోత్సవం వంటి కార్యక్రమాల ద్వారా చెట్లను నాటి తరిగిపోతున్న అడవులను రక్షించవచ్చు.
- ‘చెట్టు-నీరు’ వంటి సామాజిక కార్యక్రమాలు చేపట్టి వృక్షసంపద ‘పించవచ్చు.
- ఇంకుడు గుంటలు నిర్మించి, భూగర్భజలం పెంచవచ్చు.
- ప్రతి పుట్టినరోజున మొక్కను నాటటం అలవాటుగా మార్చాలి.
ప్రశ్న 29.
పెద్ద పెద్ద వృక్షాలను ఒక చోటనుండి మరొకచోట ,నాటటానికి ఉపయోగించే సాంకేతిక విజ్ఞానం గురించిన సమాచారం సేకరించి చర్చించండి.
జవాబు:
- పెద్ద వృక్షాలను ఒకచోట నుండి మరొకచోటకు తరలించే విజ్ఞానం మొక్కలపాలిట వరం వంటిది.
- ఈ ప్రక్రియలో హైడ్రాలిక్ యంత్రాలు, ప్రొక్లెయిన్స్, మూవర్స్ వంటి యంత్రపరికరాలు వాడతారు.
- ముందుగా మొక్కను తిరిగి నాటవలసిన ప్రదేశాన్ని ఎన్నుకొని మొక్క పరిమాణం ఆధారంగా హైడ్రాలిక్ యంత్రాలలో శంఖు ఆకారపు గోతి తవ్వుతారు.
- తరువాత మొక్కను వేరు వ్యవస్థ పాడవకుండా చుట్టూ ఉన్న మట్టితో సహా హైడ్రాలిక్ యంత్రాల సహాయంతో తవ్వుతారు.
- ఇలా తవ్వటం చెట్టు పరిమాణం దాని విస్తీర్ణంపై ఆధారపడి ఉంటుంది. చెట్టు కాండం నుండి నిర్దిష్ట దూరంలో పార వంటి పెద్ద యంత్రపలకలు కల్గిన మూవర్ చెట్టును మట్టితో సహా పెకిలించి లారీ వంటి నిర్మాణంపై ఉంచుతుంది.
- మూవర్ చెట్టును తనపైన ఉంచుకొని, దానిని నాటవలసిన స్థానానికి చేర్చి, ముందుగా తీసి ఉన్న గుంతలో మొక్కను ఉంచుతుంది.
- తిరిగి నాటిన మొక్క చుట్టూ, ఖాళీ ప్రదేశంలో మట్టిని చేర్చి నీరు పెట్టి మొక్కకు పోషణ చేకూర్చుతారు.
- ఈ ప్రక్రియ వలన సంవత్సరాలు తరబడి పెరిగిన పెద్ద వృక్షాలను సంరక్షించవచ్చు.
10th Class Biology Textbook Page No. 244
ప్రశ్న 30.
కొత్తపల్లి గ్రామాన్ని ఉదాహరణగా తీసుకొని ఆ గ్రామస్తులు మరియు ఇతర సంస్థల పాత్రను చర్చించండి.
జవాబు:
ఎన్నో జాతీయ, అంతర్జాతీయ సంస్థలు గ్రామీణ అభివృద్ధికి కృషి చేస్తున్నాయి. రైతు దేశానికి వెన్నెముకగా గుర్తించి, రైతు అభివృద్ధికి సహకరిస్తున్నాయి.
హైదరాబాద్ లోని ICRISAT వంటి సంస్థ దేశీయ వంగడాలపై పరిశోధన జరుపుతూ అధిక దిగుబడినిచ్చే వంగడాలకు కృషి చేస్తున్నాయి. రైతులకు నూతన వ్యవసాయ విధానాలపై అవగాహన పెంపొందిస్తున్నాయి. ప్రభుత్వాలు డ్రిప్ ఇరిగేషన్ పై 50% రాయితీలు ఇస్తున్నాయి.
IUCN అనే సంస్థ ప్రమాదం అంచున ఉన్న వన్యజాతులను, జాతీయ ఉద్యానవనాలను, సంరక్షణ, కేంద్రాలను పర్యావరణానికి సంబంధించిన అంశాల స్థాయిని పరిశీలిస్తుంది.
![]()
ప్రశ్న 31.
అంతర్జాతీయ, జాతీయ, రాష్ట్ర సంస్థలు మాత్రమే వనరుల యాజమాన్యంలో పాత్ర వహిస్తాయా? ఈ యాజమాన్య ప్రక్రియ మొత్తంలో ఎవరెవరు పాల్గొంటారు?
జవాబు:
వనరుల యాజమాన్యం కేవలం అంతర్జాతీయ, జాతీయ, రాష్ట్ర సంస్థలకు మాత్రమే పరిమితం కాదు. ఈ ప్రక్రియలో సమాజాన్ని, పౌరులను బాధ్యులుగా చేసినపుడు వనరుల యాజమాన్యం సక్రమంగా నిర్వహించబడుతుంది. వనరుల యాజమాన్యాన్ని ప్రతి పౌరుడూ బాధ్యతగా చేపట్టాలి. దీనికోసం ఆయా సంస్థలు ప్రజలలో వనరుల వినియోగం మీద వాటి ఫలితాలపైన పూర్తి అవగాహన కల్పించాలి. పెద్ద ఎత్తున ప్రజలలో, చర్చా కార్యక్రమాలు, వేదికలు ఏర్పాటు చేసి ప్రచారం చేపట్టాలి. వనరుల వినియోగంపైన రేపటి పౌరులైన బాలబాలికలకు అవగాహన పెంచాలి. వనరుల అంశాలను పాఠ్యాంశముగా బోధించాలి. ‘వనరుల సంరక్షణే – దేశ రక్షణ’ అని తెలియజెప్పాలి.
ప్రశ్న 32.
నీవు, నీ స్నేహితులు ఏ ఏ మార్గాల ద్వారా వనరులను సంరక్షిస్తారు? ప్రకృతిలో మనం కూడా ఒక ప్రధాన వనరేనా? ఏవిధంగా?
జవాబు:
- ఇంకుడు గుంటలు నిర్మించి నీటి వనరులను సంరక్షిస్తాము.
- వృథా నీటిని తోటకు మళ్ళించి నీరు ఆదా చేస్తాము.
- పాఠశాలలో, ఇంటి ఆవరణలో పెద్ద చెట్లను పెంచి మొక్కలను సంరక్షిస్తాము.
- ఆట స్థలంలో గడ్డి మొక్కలు పెంచి నేల క్రమక్షయం నివారిస్తాము.
- ఆటస్థలం చుట్టూ రక్షణ కొరకు, థెరీసిడియం మొక్కలు పెంచుతాము.
ప్రకృతిలో మనం కూడా ఒక ప్రధాన వనరే. దేశ అభివృద్ధి అంతా మానవ వనరుల వినియోగం పైనే ఆధారపడి ఉంటుంది. ఏ దేశంలో మానవ వనరులు పుష్కలంగా ఉంటాయో ఆ దేశానికి అభివృద్ధి అవకాశాలు ఎక్కువ. అయితే ఈ మానవ వనరులను సక్రమంగా, బాధ్యతాయుతంగా వినియోగించగలగాలి. అది సాధ్యం కానప్పుడు అధిక జనాభా వలన దేశం పేదరికంలోనికి నెట్టబడుతుంది.
ప్రశ్న 33.
మీ ఇంట్లో రోజుకు ఎన్ని లీటర్ల నీటిని వాడుతున్నారో కనుక్కోండి. అన్ని నీళ్ళు వాడడం అవసరమా? జాతీయ ప్రమాణాల ప్రకారం ఎంత నీరు అవసరం?
జవాబు:
మా ఇంటిలో రోజుకు 250 లీటర్ల నీటిని వాడుతున్నారు. వాస్తవానికి ఇంత నీరు అవసరం లేదు. నీటిని పొదుపుగా వాడుకొన్నట్లయితే 200 లీటర్ల నీరు సరిపోతుంది. అంటే రోజుకు సరాసరి 50 లీటర్ల నీటిని పొదుపు చేయవచ్చు.
10th Class Biology 10th Lesson సహజ వనరులు Textbook Activities (కృత్యములు)
కృత్యం – 1
మీరు నివసిస్తున్న పరిసరాలలో ఏ విధంగా నీరు ఉపయోగించబడుతోంది? దుర్వినియోగం చేయబడుతోందో మరియు పునఃచక్రీయం చేయబడుతుందో అధ్యయనం చేయండి. సహ విద్యార్థులు, ఉపాధ్యాయుల సహాయంతో ప్రశ్నావళిని రూపొందించి, ఐదు ఇళ్లను అధ్యయనం చేయండి. అందరికీ నీరు అందించే విధానాలను అన్వేషించి చర్చించండి.
జవాబు:
1. నీటి వినియోగం :
- ఇంటిలో నిత్య అవసరాలకు
- వ్యవసాయంలో పంట పొలాలకు
- జల విద్యుత్ తయారీకి నీరు వినియోగిస్తున్నారు.
2. దుర్వినియోగ సందర్భాలు :
- గృహ వినియోగంలో చాలా నీరు దుర్వినియోగం అవుతోంది.
- వాడిన నీరు వృథాగా కాలువలలో చేరుతోంది. ఈ నీటిని ఇతర ప్రక్రియలకు, మొక్కలు పెంచటం వంటి వాటికి వాడవచ్చు.
- వ్యవసాయంలో కాలువల ద్వారా నీటి సరఫరా జరుగుతోంది. ఈ ప్రక్రియలో చాలా నీరు వృథా అవుతోంది.
- పంట భూముల నుండి నీటిని అధికంగా వృథా చేస్తున్నారు. రసాయన ఎరువు వలన కలుషితం అవుతోంది.
- చెరువుల నుండి నీరు ఆవిరిగా మారి వృథా అవుతోంది.
- పంట కాలువల యాజమాన్యం సరిగా లేక నీటి వృథా జరుగుతోంది.
3. పునఃచక్రీయం :
పంట కాలువ మీద ఆనకట్ట కట్టి మినీ హైడల్ ప్రాజెక్టు నిర్వహిస్తున్నారు. విద్యుత్ ఉత్పత్తికి ఉపయోగించిన నీటిని తిరిగి పంటకాలువలకు పంపి పునర్వినియోగం చేస్తున్నారు.
ప్రశ్నావళి :
- మీ ఇంటిలో ఎంత మంది సభ్యులు ఉన్నారు?
- రోజుకు ఎంత నీరు వాడుతున్నారు?
- మీకు ఉన్న నీటి వనరులు ఏమిటి?
- నీటి ఎద్దడి ఉన్నప్పుడు ఏం చేస్తారు?
- నీటిని పొదుపు చేయవచ్చు అని మీరు భావిస్తున్నారా?
- తక్కువ నీటి వినియోగానికి మీరు తీసుకొనే జాగ్రత్తలు ఏమిటి?
కృత్యం – 2
మీ ఇంట్లో, పరిసర ప్రాంతాలలో ఎన్ని రకాల కీటకాలున్నాయో కనుక్కోండి. అన్ని కాలాలలో ఒకే రకమైన కీటకాలు ఉంటాయా? కీటకాల పేర్లను చార్టుపై రాయండి (కీటకాల పేర్లు తెలియకపోతే పెద్దవారిని అడిగి తెలుసుకోండి). ప్రతి కాలంలో, వారానికొకసారైనా కీటకాల ఉనికిని నమోదు చేయండి. అన్ని కాలాల్లో ఈ కృత్యాన్ని చేస్తూ ఒక సంవత్సర కాలం అధ్యయనం చేయండి. ఎప్పుడు ఎక్కువ రకాల కీటకాలు కనిపిస్తున్నాయో కనుక్కోండి. తరవాత సంవత్సరాలలో ఆ కీటకాలేమైనా అదృశ్యమయ్యాయా అధ్యయనం చేయండి.
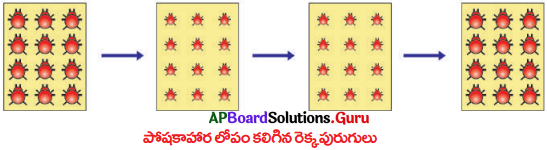
జవాబు:
- మా ఇంటి పరిసరాలలో ఈగ, దోమ, గొల్లభామ, సాలీడు, కొంకి పురుగు, బొద్దింక, తూనీగ, సీతాకోకచిలుక, మిడుత, రెక్కల పురుగు, మాత్, వడ్లచిలక వంటి కీటకాలు ఉన్నాయి.
- అన్ని కాలాల్లో ఒకే రకమైన కీటకాలు ఉండుటలేదు.
- వర్షాకాలంలో, ఇళ్లలో కనిపించే కీటకాలు అధికంగా ఉంటే శీతాకాలంలో పంటపొలాలపై కనిపించే కీటకాలు అధికంగా ఉండటం గమనించాను. వేసవి కాలంలో ఈగలు అధికంగా ఉండటం గమనించాను. పండ్ల రంగు ఆయా కాలాన్ని బట్టి మారుతూ ఉండటం గమనించాను.
- అన్ని కీటకాలు ప్రతి సంవత్సరం కనిపించుట లేదు. కొన్ని కీటకాలు అదృశ్యమవుతున్నాయి. దీనికి వాతావరణ పరిస్థితులలో, మార్పులు కారణమవుతున్నాయి. పరిస్థితులు అనుకూలించినపుడు మరలా మాయమైన కీటకాలు కనిపించటం ఆశ్చర్యం కలిగించింది.
కృత్యం – 3
ఈ రోజుల్లో ప్రజలు తవ్వకాల పట్ల సుముఖంగా లేరు. తవ్వకాలు జరుగుతున్న ప్రాంతాల్లో ప్రజలు తిరగబడుతున్నారు. ఇలాంటి సంఘటనలను గ్రంథాలయం లేదా వార్తా పత్రికల నుండి సేకరించి, ఖనిజాల తవ్వకాల ప్రభావంపై సెమినార్ ఏర్పాటు చేయండి.”
అభివృద్ధి పేరిట, పారిశ్రామికీకరణ పేరిట, చాలా సహజవనరులను, ప్రకృతిని మానవుడు ధ్వంసం చేస్తున్నాడు. అదృష్టం కొలది వీటి పరిణామాలపై మానవులలో అవగాహన పెరిగింది. ప్రకృతి వ్యతిరేక చర్యలను ప్రజలు ఖండిస్తున్నారు.
- తీర ప్రాంతాలలో ఇసుక తవ్వకాలను ప్రజలు వ్యతిరేకిస్తున్నారు.
- కడప ప్రాంతంలో అణుశుద్ధి కర్మాగార స్థాపన పెద్ద ఎత్తున నిరసనను ఎదుర్కొంది.
- కృష్ణా, గోదావరి బేసిన్లో ఆయిల్ తవ్వకాలను ప్రజలు వ్యతిరేకించారు.
- కర్ణాటకలోని బయ్యారం ఇనుప ఖనిజ తవ్వకాలపై నిరసన వచ్చింది.
- ఖనిజ నిల్వల కోసం, ఇతర అవసరాల కోసం అడవుల నరికివేత తీవ్ర విమర్శలకు లోనైంది.
- ఆనకట్టల కోసం తవ్వకాలను, అడవుల నిర్మూలనను ప్రజలు ఖండిస్తున్నారు.
- తెక్రీడ్యామ్ నిర్మాణాన్ని సుందర్లాల్ బహుగుణ తీవ్రంగా వ్యతిరేకించి ఉద్యమం నడిపాడు.
- పర్యావరణ పరిరక్షణ కోసం మన రాష్ట్రంలో తెలుగుగంగ ప్రాజెక్టు మార్గాన్ని మార్చారు.
ఈ ఉద్యమం ప్రజలలో పర్యావరణంపై ఉన్న అభిమానాన్ని, చైతన్యాన్ని తెలియజేస్తుంది. ఇది అభినందనీయ మార్పు. స్వాగతించవలసిన పరిణామం.
కింది ఖాళీలను పూరించండి
1. జీవ ఇంధన ఉత్పత్తికి ……. మొక్కలను ఉపయోగిస్తారు. (జట్రోప)
2. జీవవైవిధ్యాన్ని కాపాడుకోవడం ఆహారం కోసమే కాదు …………….. కోసం కూడా. (ఔషధాల)
3. తరిగిపోని ఇంధన వనరుకు ఉదాహరణ ………. (గాలి, నీరు)
4. భూగర్భజలాలు తగ్గిపోకుండా కాపాడుకోడానికి అనుసరించదగిన ఒక ప్రత్యామ్నాయ పద్ధతి ………… (ఇంకుడు గుంట)
5. వరిసాగు …………….. ప్రదేశాలకు అనువైనది. (అధికనీరు ఉన్న)
సరైన సమాధానాన్ని గుర్తించండి
1. ఇంకుడు గుంటల వలన ఉపయోగం
A) వ్యవసాయానికి నీరు అందించడం
B) భూగర్భజల మట్టాలు పెంచడం
C) వర్షపు నీటిని నిల్వచేయడం
D) వర్షాకాలంలో వచ్చే వరదలను అరికట్టడం
జవాబు:
B) భూగర్భజల మట్టాలు పెంచడం
2. తక్కువ నీటి సౌకర్యాలు ఉన్న ప్రాంతాలలో రైతులు అనుసరించదగిన విధానం
అ) స్వల్పకాలిక పంటలు పండించడం
ఆ) వ్యాపార పంటలు పండించడం
ఇ) బిందుసేద్యం చేయడం
ఈ) పంట విరామం ప్రకటించడం
A) అ, ఆ
B) అ, ఆ, ఇ
C) అ,ఈ
D) ఇ,ఈ
జవాబు:
B) అ, ఆ, ఇ
3. భారతదేశంలో అతివేగంగా అంతరించిపోతున్న ఇంధన వనరులు –
A) సహజవాయువు
B) బొగ్గు
C) పెట్రోలియం
D) అన్ని
జవాబు:
D) అన్ని
4. పరిసరాలలోకి హానికర రసాయనాలు పెద్దమొత్తంలో విడుదల కావడానికి కారణం
A) పరిశ్రమలు
B) గనులు
C) క్రిమిసంహారకాలు
D) ఆధునిక సాంకేతికత
జవాబు:
A) పరిశ్రమలు
![]()
5. సుస్థిర అభివృద్ధి అనగా
A) వృథాను అరికట్టడం
B) స్థిరమైన పెరుగుదల
C) నష్టం వాటిల్లకుండా అభివృద్ధి చేయడం
D) తక్కువ సమయంలో ఎక్కువ ఉత్పత్తి చేయడం
జవాబు:
C) నష్టం వాటిల్లకుండా అభివృద్ధి చేయడం