AP 10th Class Maths Bits Chapter 2 Sets with Answers

Practice the AP 10th Class Maths Bits with Answers Chapter 2 Sets on a regular basis so that you can attempt exams with utmost confidence.

AP SSC 10th Class Maths Bits 2nd Lesson Sets with Answers

Question 1.
Which type of set of human being that reside on moon is ……………….
Answer:
null set

Question 2.
Write the number of subsets of the null set Φ.
Answer:
1

Question 3.
Ifn(A) = 8, n(B) = 3, n(A ∩ B) = 2, then find n(A ∪ B).
Answer:
9
Explanation:
n(A∪B) = n (A) + n (B) – n (A ∩ B)
= 8 + 3-2 = 9

Question 4.
The number of subsets of a set is 16, then find the set has ………… elements.
Answer:
4
Explanation:
2ⁿ = 16 = 2⁴
⇒ no. of elements in the set = 4

Question 5.
Write the number of subsets of the set A = {l, 2,3, 4}.
Answer:
16
Explanation:
n (A) = 4, no. of subsets = 2ⁿ = 2⁴ = 16

Question 6.
If A⊂ B, n(A) = l2and n(13) = 20, then find the value of n (B – A).
Answer:
8
Explanation:
A ⊂ B, son (B – A) = 20- 12 .= 8

Question 7.
Roster form of (x: x is a prime number and a divisor of 6).
Answer:
{2,3}

Question 8.
Write an example for finite set in your own.
Answer:
{x/x∈N and x² = 9}

Question 9.
If A⊂B,n(A) = 4 and n(B) = 6,then find n(A∪ B).
Answer:
6
Explanation:
A ⊂ B, so n (A ∪ B) = n (B) = 6

Question 10.
If A⊂B, then A∩B is
Answer:
A
Explanation:
A⊂B, so A∩B = A

Question 11.
If the union of two sets is one of the set itself, write the relation between the two sets.
Answer:
One set is a subset of other set.

Question 12.
The following venn diagram indicates

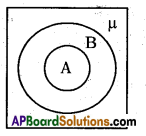
Answer:
A⊂B

Question 13.
If A From the venn diagram, find A ∪ B.

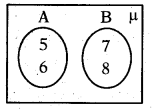
Answer:
{5, , 7, 8}

Question 14.
If A = {x : x is a letter in the word EX¬AMINATION}, then write its roster form.
Answer:
A = {e, x, m, i, n, a, t, o}

Question 15.
If A = {x : x is a letter in the word HEADMASTER}; then write its ros-ter form.
Answer:
A — {h, e, a, d, m, s, t, r}

Question 16.
If n (A) = 12 and n (A ∩ B) = 5, then find n (A – B).
Answer:
7
Explanation:
n (A – B) = n(A) – n(A∩B) = 12 – 5 = 7

Question 17.
The following venn diagram indicates

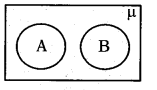
Answer:
A, B are disjoint sets.

Question 18.
The shaded region in the given figure shows.

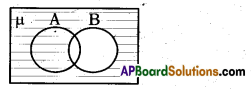
Answer:
μ – B = B’

Question 19.
Write the relation between sets in the following venn diagram.

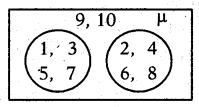
Answer:
A ∩ B = Φ

Question 20.
If A ={1,2, 3}, B = (3,4, 5), then find A Δ B.
Answer:
A Δ B = {1,2, 4, 5}
Explanation:
A Δ B = (A ∪ B) – (A ∩ B)
= {1, 2, 3, 4, 5}- {3} = {1,2, 4, 5}

Question 21.
(A’)’is equal to …………….
Answer:
A

Question 22.
An object of a set is called ……………..
Answer:
Element

Question 23.
2 is ………………. of set of natural numbers.
Answer:
An element

Question 24.
Number of elements in a singleton set is …………………..
Answer:
1

Question 25.
If A, B are disjoint sets such that n (A) = 4 and n (A ∪ B) = 7, then find n(B).
Answer:
3
Explanation:
n(A∪B) = n (A) + n (B) – n (A ∩ B)
⇒ 7 = 4 + n (B) – 0
⇒ n(B) = 7 – 4 = 3

Question 26.
‘O’ is to set of whole numbers.
Answer:
belong

Question 27.
n (A) = 4, then write n(p(A)).
Answer:
16
Explanation:
n(P(A)) = 2ⁿ = 2⁴ = 16

Question 28.
If A = {1, 2, 3} and B = {1, 2, 3, 4}, then we say A is a …………….. of B.
Answer:
Subset

Question 29.
Φ is equal to A.
Answer:
μ

Question 30.
A set is a ……………… of objects.
Answer:
Well defined collection.

Question 31.
{2, 4,6, 8, 10} is an example of which type of set ?
Answer:
Finite

Question 32.
If A = {1, 2, 3, 4}, B = {2, 4, 6, 8}, then find A – B.
Answer:
{1,3}

Question 33.
A = {2, 4, 6, 8, 10}, then write its rule form.
Answer:
A = {x / x is an even number, x ≤ 10}

Question 34.
If B = {1, 7, 2, 0, 6}, then find n(B).
Answer:
5

Question 35.
A – (A -B) is equal to ……………..
Answer:
A ∩ B

Question 36.
The objects in the set are called ……………….. of the set.
Answer:
Elements

Question 37.
Let A, B are two sets such that n (A) = 5, n(B) = 7, then write the maximum number of elements in A ∪ B.
Answer:
12

Question 38.
Empty set is denoted by ………………..
Answer:
Φ

Question 39.
Write A Δ B.
Answer:
(A – B) ∪

(B – A) (or) (A∪B)-(A ∩ B)

Question 40.
A = {1, 2, 3}, B = {3, 4, 5}, then find A ∩ B.
Answer:
{3}

Question 41.
– 3 is of the set of whole numbers.
Answer:
not an element

Question 42.
If n(A ∪ B) = 8, n(A) = 6, n(B) = 4, then find n(A ∩ B).
Answer:
2

Question 43.
The number of elements in a set is called the…………….of the set.
Answer:
Cardinal number

Question 44.
A ∪ Φ is equal to …………………
Answer:
A

Question 45.
{x / x ≠ x} is which type of set ?
Answer:
Empty

Question 46.
B = {x/x ∈ N and x < 1000} is a ……………type of set.
Answer:
Finite

Question 47.
Write the symbol used for belongs to’.
Answer:
∈

Question 48.
n (Φ) is equal to ………………..
Answer:
0

Question 49.
Write (2, 6, 10} ∩ (8, 9, 11, 12, 13}.
Answer:
Φ

Question 50.
{x / x is a student of your school} is in which form ?
Answer:
Set Builder

Question 51.
Every set is ……………. of itself.
Answer:
Subset

Question 52.
A = {1, 2,7, 10}, then use symbol be-tween 7 and A.
Answer:
∈

Question 53.
If A = {1, 2, 3, 4}, then find the cardi-nality of set A.
Answer:
4

Question 54.
A≠B means, set A and B do not contains same elements. This statement is true (or) false.
Answer:
True

Question 55.
A = {1, 2, 3}, B = {12, 0, 5}, then find A-B.
Answer:
A

Question 56.
A = {x / x + 4 = 4}, then write Roster form of A.
Answer:
{0}

Question 57.
Which type of set has no elements in it ?
Answer:
Null set

Question 58.
If A ∪ B = A ∪ C and A ∩ B = A ∩ C, then write the relation between these sets.
Answer:
B = C

Question 59.
A set with only one element is known as ……………. set.
Answer:
singleton

Question 60.
The set of all real numbers is, which type of set ?
Answer:
Infinite set

Question 61.
Roster form of B = \(\left\{\frac{x}{x}+3=6\right\}\), B = ?
Answer:
{3}

Question 62.
‘μ’ is equal to
Answer:
Φ

Question 63.
If A ⊂ B and A ≠ B, then A’ is called the ………………. of B.
Answer:
Proper subset

Question 64.
{x / x is a natural number} is which type of set ?
Answer:
Infinite

Question 65.
Write the number of elements in the empty set.
Answer:
0

Question 66.
The null set is sometimes denoted as .
Answer:
{} = Φ

Question 67.
If in two sets A and B, every element of A is in B and every element of B is in A, then write it as
Answer:
A = B

Question 68.
Another name to Roster form is ……………….
Answer:
List

Question 69.
A’ – B’ is equal to
Answer:
B-A

Question 70.
If every element of A is also an element of B, then write this symboliically.
Answer:
A⊂B

Question 71.
A ⊂ B, then find A – B.
Answer:
Φ

Question 72.
“0 does not belong to the set of natural numbers”. Write the statement sym¬bolically.
Answer:
0 ∉ N

Question 73.
A = {1,2, 4}, B = {3, 5, 6}, then write the relation.
Answer:
A ∩ B = Φ

Question 74.
If A ⊂ B, then find A ∪ B.
Answer:
B

Question 75.
If B = {1,7, 2, 0,6}, then find n(B).
Answer:
5

Question 76.
Write Roster form of the set of natu¬ral numbers less than 6.
Answer:
(1, 2, 3, 4, 5}

Question 77.
If A ⊂ B, then find A-B.
Answer:
Φ

Question 78.
A ∪ Φ is equal to ……………
Answer:
A

Question 79.
A ∪ B = B ∪ A is called ……………. law.
Answer:
Commutative

Question 80.
If A = {1, 2, 2, 1, 3, 4, 3, 4}, then find n(A).
Answer:
4

Question 81.
Write cardinal number of null set.
Answer:
0

Question 82.
K = {x/x is a prime number less than 13}. Write list form of K.
Answer:
K= {2, 3, 5, 7, 11}

Question 83.
W – {0} is equal to …………………
Answer:
N

Question 84.
In the rule form, the slant bar stands for
Answer:
such that

Question 85.
A = {a, b, c}, B = {c, a, b}, then write the relation between A and B.
Answer:
A – B

Question 86.
Write the set formed from the letters of the word “SCHOOL “.
Answer:
{S, C, H, O, L}

Question 87.
A = {1, 2, 7}, B = {2, 1}, then write the relation between A and B.
Answer:
B⊂A

Question 88.
If A ⊂ B, B ⊂ C, then write the relation between A and C.
Answer:
A ⊂ C

Question 89.
If A ⊂ B, then find A∪(B – A).
Answer:
B

Question 90.
Write the set builder form of D = \(\left\{1, \frac{1}{2}, \frac{1}{3} ; \frac{1}{4}, \frac{1}{5}, \frac{1}{6}\right\}\)
Answer:
D = {x / x ∈ 1/n ,n ∈ N,n < 7}

Question 91.
In set builder form, the letter “X” denotes any………… that belongs to the set.
Answer:
Arbitrary element.

Question 92.
Write the Roster form of the set of multiples of 5 which lie between 25 and 50 is
Answer:
{30, 35, 40, 45}

Question 93.
Write the name of German mathemati¬cian who developed the theory of sets.
Answer:
George Cantor.

Question 94.
N∩W is equal to ………………..
Answer:
N

Question 95.
A = Φ, B = Φ, then find A∩B.
Answer:
Φ

Question 96.
Write the identity element under union of sets.
Answer:
Φ

Question 97.
A ∩ B = Φ, then find B ∩ A’.
Answer:
B

Question 98.
A = {all primes less than 20}
B = {all whole numbers less than 10}, then find A∩B.
Answer:
{2,3, 5, 7}

Question 99.
μ’ = Φ is called …………….. law.
Answer:
Complementary

Question 100.
A ∪ A = A is called……………law.
Answer:
Idempotent.

Question 101.
If A and B are disjoint sets, then write n (A ∪ B).
Answer:
n (A) + n (B)
Explanation:
n (A ∪ B) = n (A) + n (B)

Question 102.
If A = Φ, B = Φ, then find A∪B.
Answer:
Φ

Question 103.
n (A) = 3, then write the number of proper subsets of A.
Answer:
7
Explanation:
Proper subsets are 2ⁿ – 1 = 2³ – 1
= 8 – 1
= 7

Question 104.
A ∪ B = A ∩ B, then write the relation between A and B.
Answer:
A = B

Question 105.
n (A ∪ B) = 51, n (A) = 20, n (A ∩ B) = 13, then find n (B).
Answer:
44
Explanation:
n (A ∪ B) = n (A) + n (B) – n (A ∩ B)
⇒ 51 = 20 + n(B)- 13
⇒ 31 + 13 = n(B) = 44

Question 106.
A’ = B, then find A ∪ B.
Answer:
μ
Explanation:
A’= B ⇒ μ – A = B
⇒ A u B = μ

Question 107.
n (A) = 10, n (B) = 4, n (A ∩ B) = 2, then find n (A ∪ B).
Answer:
12

Question 108.
μ ∪ Φ is equal to
Answer:
μ

Question 109.
If A ∩ B = Φ then find n (A ∩ B).
Answer:
n (A) + n (B)

Question 110.
Write the identity element under intersection of sets.
Answer:
μ

Question 111.
A∪B = B, then write the relation between A and B.
Answer:
A⊂B

Question 112.
The given venn diagram represents.

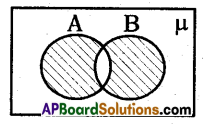
Answer:
AΔB

Question 113.
Φ Δ Φ is equal to
Answer:
Φ

Question 114.
(A ∪ B)’ is equal to
Answer:
A’ ∩ B’
Explanation:
(A ∪ B)’ = A’∩B’

Question 115.
Draw the venn diagram of A – B.
Answer:

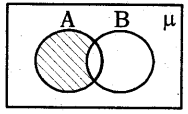
Question 116.
If the number of proper subsets of a given set is 31, then how many ele-ments the set contains ?
Answer:
5
Explanation:
2ⁿ – 1 = 31 ⇒ 2ⁿ = 32 = 2⁵
∴ no. of elements are 5.

Question 117.
Write the intersection of set of ratio-nal numbers and set of irrational num¬bers.
Answer:
Real numbers

Question 118.

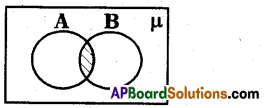
This venn diagram represents
Answer:
A∩B

Question 119.
From the venn diagram, write the set A∪B.

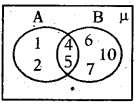
Answer:
A ∪ B = {1, 2, 4, 5, 6, 7, 10}
Explanation:
A ∪ B = {1,2, 4, 5, 6, 7, 10}

If A = {x : x is a natural number}
B = {x : x is an even natural number}
C = {x : x is an odd natural number) and
D = {x : x is a prime number}

Question 120.
Find A∩B.
Answer:
A∩B = (1, 2, 3, 4, } ∩ (2, 4, 6, 8…………… }
= {2,4,6, 8, ….} = B{∵B⊂A}

Question 121.
Find A ∩C.
Answer:
A ∩ C = {1, 2, 3,4, …} ∩ {1, 3, 5, 7,…} = (1,3, 5, 7,…} = C(∵C⊂A}

Question 122.
Find A ∩D.
Answer:
A∩D = {1,2, 3, 4, …} ∩ {2, 3,5,7,…} = {2, 3, 5, 7,…} = D{∵ D⊂A)

By observing the below diagram and answer the following questions :

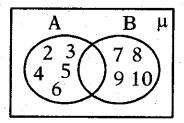
Question 123.
Find A∪B.
Answer:
A∪B = {2, 3, 4, 5, 6} ∪ {7, 8, 9, 10} = {2,3,4,5,6,7,8,9,10}

Question 124.
Find A∩B.
Answer:
A∩B = {2, 3, 4, 5, 6} ∩ {7, 8, 9, 10}
= { } = Φ

Question 125.
Find A Δ B.
Answer:
A Δ B = (A ∪ B) – (A ∩ B) = A ∪ B . { ∵ A ∩ B = Φ}

By observing the below diagram and answer the following questions.

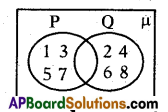
Question 126.
What do you observes in P and Q ?
Answer:
There are no common elements

Question 127.
Name the type of sets P and Q.
Answer:
P and Q are disjoint sets.

Question 128.
Write the relation between P and Q.
Answer:
P ∩ Q = Φ

Question 129.
Define disjoint sets.
Answer:
There is no common elements in any two sets such type of sets are called disjoint sets.

By observing the below information and answer the following questions.

D = The set of all letters in the word TRIGONOMETRY

Question 130.
Write the Roster form of set ‘D’.
Answer:
D = {T, R, I, G, O, N, M, E, Y}

Question 131.
Write the cardinal number of set D.
Answer:
n (D) = 9
By observing the below diagram and answer the following questions.

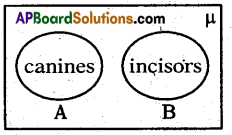
Question 132.
Find n(A).
Answer:
n (A) = 2

Question 133.
Find n(B).
Answer:
n (B) = 1

Question 134.
Find n(A ∩ B).
Answer:
n(A ∩ B) = Φ

Question 135.
Find n(A ∪ B).
Answer:
n(A ∪ B) = 3

Question 136.
Write the relation between n (A), n (B), n (A ∩ B) and n (A ∪ B).
Answer:
n (A) + n (B) = n(A∪B) + n(A∩B)
1 + 2 = 3 + 0 = 3

Write the correct matching options.

Question 140.
Roster form
A) {a, e, i, o, u} []
B) {2, 5, 10, 17} []

Choose the correct answer satistying the following statements.

Question 137.
Statement (A): If A = {1,2,3, 4, 5,6}, B = {7,8,9, 10, 11} and C = {6,8, 10, 12,14}, then A and B are disjoints sets.
Statement (B) : Two sets A and B are said to be disjoint, if A ∩ B = Φ
i) Both A and B are true
ii) A’ is true, ‘B’ is false
iii) A is false,’B’is true
iv) Both A and B are false
Answer:
i)

Question 138.
Statement (A) : The set of all rect-angles in contained in the set of all squares.
Statement (B) : The sets P = {a} and B = {{a}} are equal.
i) Both A and B are true
ii) A is true, ‘B’ is false
iii) A’ is false, ‘B’ is true
iv) Both A and 6 are false
Answer:
ii)

Question 139.
Statement (A) : For any two sets A and B, we have A – B = {x : x ∉ A and x∈B}
Statement (B) : For any two sets A and B, we have A-B = {x:x∈A and x∉B) andB-A = {x:x ∈ B and x ∉ A}
i) Both A and B are true
ii) A’ is true, ‘B’ is false
iii) A’ is false, ‘B’ is true
iv) Both A and B are false
Answer:
iii)

Write the correct matching options.

Question 140.
Roster form

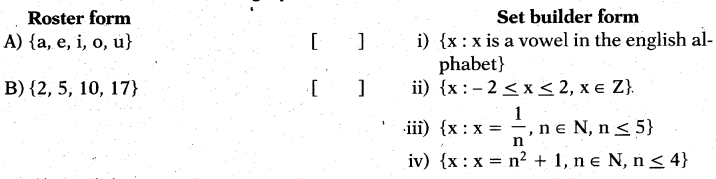
Answer:
A – (i), B – (iv).

Question 141.

Answer:
A – (iii), B – (ii).

Question 142.

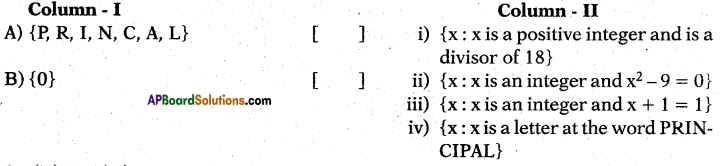
Answer:
A – (iv), B – (iii).

Question 143.

Answer:
A – (i), B – (ii).

Question 144.

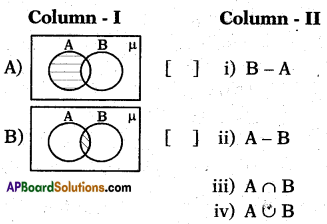
Answer:
A – (ii), B – (iii).

Question 145.

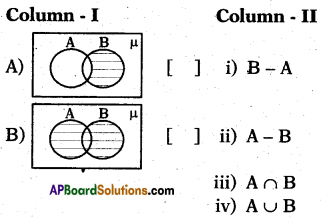
Answer:
A – (i), B – (iv).

Question 146.
If A = {1,2,3} and Φ = { }, find A∩Φ
Answer:
Φ

Question 147.
Find n(A ∪ B) from the figure

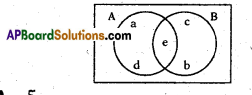
Answer:
5

Question 148.
How many subsets does a set of three distinct elements have ?
Answer:
8 sub-sets

Question 149.
If A = {1,2,3} andB = {2,4,6}. What is n(A ∪ B) ?
Solution:
A = {1, 2, 3}, B = {2, 4, 6}
A∪B = {1, 2, 3}∪{2, 4,6} = {1,2,3,4,61
n(A ∪ B) = 5