AP 10th Class Maths Bits Chapter 4 Pair of Linear Equations in Two Variables with Answers

Practice the AP 10th Class Maths Bits with Answers Chapter 4 Pair of Linear Equations in Two Variables on a regular basis so that you can attempt exams with utmost confidence.

AP SSC 10th Class Maths Bits 4th Lesson Pair of Linear Equations in Two Variables with Answers

Question 1.
Pair of equations 4x + 6y = 7 and 2x + 3y = 8. How many solutions have ?
Answer:
No solution.

Question 2.
Find the point where the line 2x – 3y = 8 intersects X – axis ?
Answer:
(4,0)
Explanation:stitute y = 0 in 2x – 3y = 8
⇒ 2x – 3-0 = 8 ⇒ x = 4
∴ The point on X – axis = (4, 0).

Question 3.
Find the solution for the equations \(\sqrt{3} x+\sqrt{5 y}=0\) and \(\sqrt{7} \mathrm{x}+\sqrt{11} \mathrm{y}=0\)
Answer:
x = 0, y = 0.

Question 4.
Find the value of ‘x’ in the equation 3x- (x-4) = 3x + 1.
Answer:
3
Explanation:
3x – x + 4 = 3x + 1
⇒ 3x – 3x — x = 1 – 4
⇒ x = 3

Question 5.
The pair of equations a₁x + b₁y + C₁ = 0 and a₂x + b₂y + c₂ = 0 are consistent, then write the condition for that.
Answer:
\(\frac{\mathrm{a}_{1}}{\mathrm{a}_{2}} \neq \frac{\mathrm{b}_{1}}{\mathrm{~b}_{2}}\) and \(\frac{\mathrm{a}_{1}}{\mathrm{a}_{2}}=\frac{\mathrm{b}_{1}}{\mathrm{~b}_{2}}=\frac{\mathrm{c}_{1}}{\mathrm{c}_{2}}\)

Question 6.
The graph y = ax + b is a straight line, find the point x where it intersects x – axis ?
Answer:
(\(-\frac{b}{a}\), 0)

Question 7.
Find the value of ‘k’ for which the sys-tem of equations kx – y = 2 and
6x – 2y = 3 has no solution.
Answer:
3
Explanation:
\(\frac{\mathrm{a}_{1}}{\mathrm{a}_{2}}=\frac{\mathrm{b}_{1}}{\mathrm{~b}_{2}}\) when pair of equations has no solution.
\(\frac{\mathrm{k}}{6}=\frac{1}{2} \Rightarrow \mathrm{k}=\frac{6}{2}\) = 3

Question 8.
Find the point of intersection of x + y = 6 and x – y = 4.
Answer:
(5,1)
Explanation:
x + y = 6 and
x-y = 4 ⇒ x = 4 + y
4 + y + y = 6 ⇒ 2y = 2 ⇒ y = 1
x = 6 – y = 6 – 1 ⇒ x = 5 .
∴ Point of intersection (x, y) = (5, 1).

Question 9.
If pair of equations 6x + 2y – 9 = 0 and kx + y – 7 = 0 has no solution, then find ‘k’.
Answer:
3
Explanation:
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \Rightarrow \frac{6}{k}=\frac{2}{1} \Rightarrow \frac{6}{2}\) = k ⇒ k = 3

Question 10.
If the pair of equations 2x+3y+k = 0, 6x + 9y + 3 = 0 having infinite solu-tions, find the value of ‘k’.
Answer:
1
Explanation:
Infinite solutions, so

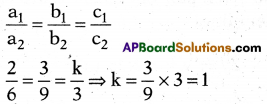
Question 11.
A pair of linear equations in two variables are 2x – y = 4 and 4x – 2y = 6. The pair of equations are
Answer:
Inconsistent.
Explanation:
\(\frac{2}{4}=\frac{1}{2} \neq \frac{4}{6} \Rightarrow \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
∴ Pair of equations are inconsistent.

Question 12.
How many solutions to the pair of equations y = 0 and y = – 3 ?
Answer:
No solution.

Question 13.
If 7x – 8y = 9, then find ‘y’.
Answer:
\(\frac{7 x-9}{8}\)

Question 14.
Write the standard form of a linear equation.
Answer:
ax + by + c = 0

Question 15.
For which value of ‘k’ will the follow-ing pair of linear equations have no solution 3x + y = 1;
(2k- l)x + (k – l)y = 2k – 1 ?
Answer:
2
Explanation:
No, solution, so \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}\)
⇒ \(\frac{3}{2 k-1}=\frac{1}{k-1}\)
⇒ 3(k – 1) = 1 (2k – 1)
⇒ 3k – 3 = 2k – 1 ⇒ 3k – 2k = 3 – 1 ⇒ k = 2

Question 16.
The lines 3x + 8y – 13 = 0 and – 6x – 16y + 23 = 0 are type of lines.
Answer:
Parallel
Explanation:
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}} \Rightarrow \frac{3}{-6}=\frac{8}{-16} \neq \frac{-13}{23}\)
∴ Parallel lines.

Question 17.
2x + 3y = 1, 3x – y = 7, then find (x, y).
Answer:
(2,-1)

Question 18.
Where the line x – y = 8 intersects X – axis ?
Answer:
(8,0)

Question 19.
x + \(\frac { 6 }{ y }\) = 6 and 3x – \(\frac { 8 }{ y }\) = 5, then find ‘y’.
Answer:
2

Question 20.
Write the nature of the graph of the line y = 5x.
Answer:
The graph of the line passes through the origin.
Explanation:
y – 5x ⇒ y = mx passes through the origin.

Question 21.
Pair of linear equations px + 3y – (p – 3) = 0, 12x + py – p = 0 has infinitely many solutions, then find p’.
Answer:
± 6.
Explanation:
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}} \Rightarrow \frac{p}{12}=\frac{3}{p}=\frac{(p-3)}{p}\)
p² = 36 ⇒ p = \(\sqrt{36}\) = ± 6

Question 22.
In which quadrant (2, 0) belongs ?
Answer:
Q₁

Question 23.
x + y = 10, x – y = – 4, then find ‘x’.
Answer:
3
Explanation:
x – y = -4 ⇒ x = y – 4 = y – 4 + y= 10
⇒ 2y – 4 = 10 ⇒ 2y = 14 ⇒ y = 7,
x – 7 = -4 ⇒ x = 7 – 4 = 3
∴ x = 3

Question 24.
Find the solution of the equations \(\sqrt{2} x+\sqrt{3} y=0\) and \(\sqrt{3} x-\sqrt{8} y=0\).
Answer:
x = 0, y = 0 (or) (0, 0)

Question 25.
If 3x + 4y + 2 = 0and9x + 12y + k = 0 represent coincident lines, then find the value of ‘k’.
Answer:
x = 0, y = 0 (or) (0.0)
Explanation:

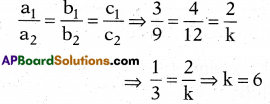
Question 26.
If ax + b = 0, then find ‘x’. b
Answer:
\(-\frac{b}{a}\)

Question 27.
If x + y = 7, x – y = 1, then find 2x.
Answer:
8
Explanation:
x – y = 1 ⇒ x = 1 + y and
x + y = 7 ⇒ 1 + y + y = 7
⇒ 1 + 2y = 7 ⇒ 2y = 6 ⇒ y = 3,
x = 1 + 3 = 4
∴ 2x = 2(4) = 8

Question 28.
If x – y = 0; 2x – y = 2, then find the value of ‘y’.
Answer:
2

Question 29.
How many solutions to the pair of lin-ear equations 3x + 4y + 5 = 0 and 12x + 16y +15 = 0 have ?
Answer:
No solution. They are parallel lines.

Question 30.
Find the solution to \(\frac{a^{2}}{x}-\frac{b^{2}}{y}=0\) ; \(\) = a + b, x ≠ 0, y ≠ 0
Answer:
(a², b²)

Question 31.
If the lines given by 3x + 2ky = 2 and 2x + 5y + 1 = 0 are parallel, then find the value of ‘k’.
Answer:
k = \(\frac{15}{4}\)

Question 32.
The lines represented by 5x + 3y – 7 = 0 and 6y + 10x – 14 = 0 are type …………… of lines.
Answer:
Coincident
Explanation:
\(\frac{5}{10}=\frac{3}{6}=\frac{7}{14} \Rightarrow \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
So given pair of equations are coinci-dent lines.

Question 33.
Find slope of the line x = 2y.
Answer:
Slope (m) = \(\frac{1}{2}\)
Explanation:
x = 2y ⇒ y = \(\frac { 1 }{ 2 }\) x ⇒ m = \(\frac { 1 }{ 2 }\)

Question 34.
If x = 1 and y = \(\frac{1}{2}\), then find x – y.
Answer:
\(\frac{3}{2}\)
Explanation:
x – y = 1 – \(\frac { -1 }{ 2 }\) = 1 + \(\frac { 1 }{ 2 }\) = \(\frac { 3 }{ 2 }\)

Question 35.
Find the value of x if y = \(\frac{3}{4}\) x and 5x + 8y = 33.
Answer:
x = 3

Question 36.
Write the slope of X – axis.
Answer:
y = 0

Question 37.
Find the value of y in – 5x + 10y =100 at x = 0.
Answer:
y = 10

Question 38.
2u + 3v = 2 and 4u – 6v = 0, then find ‘v’.
Answer:
\(\frac{1}{3}\)

Question 39.
If – x + y = – 10, then write ‘x’ as sub-ject.
Answer:
x = y + 10
Explanation:
-x + y = -10 ⇒ x = y + 10

Question 40.
Write shape of the graph of 3x-y = -1.
Answer:
Straight line.

Question 41.
The pair of linear equations
px + 2y = 5 and 3x + y = 1 has unique solution, then find value of’p’.
Answer:
p ≠ 6.
Explanation:
\(\frac{p}{3} \neq \frac{2}{1}\) ⇒ p ≠ 6

Question 42.
The lines represented by 5x + 7y – 14 = 0 and 10x + 3y-8 = 0 are……………….lines.
Answer:
Consistent.

Question 43.
3x – 5y = – 1 and – y + x = – 1, then find (x, y).
Answer:
(-2,-1).

Question 44.
How many solutions to the pair of lin-ear equations – 3x + 4y = 7 and
\(\frac { 9 }{ 2 }\) x – 6y + \(\frac { 21 }{ 2 }\) = 0 ?
Answer:
Infinitely many solutions.
Explanation:

So infinitely, many solutions.

Question 45.
For which value of ‘p’ the lines repre-sented by 8x + 2py = 2 and 2x + 5y + 1 = 0 are parallel ?
Answer:
10
Explanation:
\(\frac{8}{2}=\frac{2 p}{5}\) ⇒ P = \(\frac{8 \times 5}{2 \times 2}\) ⇒ P = 10

Question 46.
If \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\), then the lines are …………………. type of lilies.
Answer:
Coincident lines (or) dependent lines.

Question 47.
4m – 2n = 2 and 6m – 5n = 9, then find ‘n’.
Answer:
n = – 3.

Question 48.
If 99x + lOly = 499,101x+ 99y = 510, then find ‘x’.
Answer:
x = 3

Question 49.
Find the solution to x – y = 1 and 2x – 2y = 7.
Answer:
No solution (or) not possible.
Explanation:
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \Rightarrow \frac{1}{2}=\frac{1}{2}\),
so no solution.

Question 50.
141x + 93y = 189, 93x + 141y = 45, then find y’.
Answer:
y = -1

Question 51.
\(\frac{120}{x}+\frac{12}{x}\) = 11, then find ‘x’. x x
Answer:
x = 12.

Question 52.
Find the solution to 2x – 2y – 2 = 0, 4x – 4y – 5 = 0.
Answer:
No solution (or) not possible.

Question 53.
500x + 240y = 8, 130x + 240y = \(\frac{43}{10}\)
then find the value of ‘x’.
Answer:
\(\frac{1}{100}\)

Question 54.
Find the value of ‘y’ when \(\frac{x+y}{x y}\) = 2 and \(\frac{x-y}{x y}\) = 6.
Answer:
y = \(\frac { 1 }{ 4 }\)

Question 55.
Where the two lines 2x + y – 6 = 0 and 4x – 2y – 4 = 0 intersect, find that intersecting point.
Answer:
(2,2)

Question 56.
\(\frac{x+3}{2}-y=2, \frac{x-3}{2}+2 y=4 \frac{1}{2}\) then find ‘x’
Answer:
\(\frac { 14 }{ 3 }\)

Question 57.
How much the angle between any two parallel lines ?
Answer:
0°

Question 58.
Find the values of ’k’ for which the pair of linear equations 3x – 2y = 7, and 6x + ky + 11 = 0 has a unique solution.
Answer:
All numbers expect “’-“4r are the solution.

Question 59.
Find slope of the line y = x.
Answer:
m = 1

Question 60.
If x = 1, then find the value of’y’ satis- 5 3
fying the equation \(\frac{5}{x}+\frac{3}{y}\) = 6 ;
Answer:
y = 3.
Explanation:
\(\frac{5}{1}+\frac{3}{y}\) = 6 ⇒ \(\frac{3}{y}\) = 6 – 5 = 1 ⇒ y = 3

Question 61.
Write the point (- 3, – 8) is in the…………………quadrant.
Answer:
Q₃

Question 62.
Write the point (7, -5) is in the quadrant.
Answer:
Q₄

Question 63.
Find slope of the line ax + by + c = 0.
Answer:
m = \(\frac{-a}{b}\)

Question 64.
Write the nature of the line x = 2020.
Answer:
Slope not defined and it parallel to Y – axis.

Question 65.
Write the nature of the line x = 7.
Answer:
It is parallel to Y – axis.

Question 66.
Write nature of the graph of a pair of linear equations in two variables is represented by
Answer:
Straight lines.

Question 67.
Find the number of solutions to the pair of equations 6x – 7y + 8 = 0 and 12x – 14y +16 = 0.
Answer:
Infinitely many solutions.

Question 68.
If 2^x + 3^y = 17 and 2^{x + 2} – 3^{y + 1} = 5, then find y’.
Answer:
y = 2.
Explanation:
2^x + 3^y = 17
⇒ a + b = 17
⇒ 3a + 3b = 51
2^x . 2² – 3^y . 3¹ = 5
⇒ 4a – 3b = 5 ……………….. (ii)
Solving equations (1) & (2)
7a = 56 ⇒ a = 8,
b = 17-a = 17-8 = 9
3^y = b = 3² ⇒ y = 2

Question 69.
If \(\frac{2}{x}+\frac{3}{y}\) = 13 and \(\frac{5}{x}-\frac{4}{y}\) = -2
find the solution.
Answer:
( \(\frac{1}{2}, \frac{1}{3}\) )

Question 70.
If 5x + py + 8 = 0 and 10x + 15y + 12 = 0 has no solution, then find the value of
p’.
Answer:
P = 7\(\frac{1}{2}\)

Question 71.
The larger of two supplementary angles exceeds the smaller by 38°. Find them.
Answer:
71° and 109°.
Explanation:
x, 180 – x =⇒ y = 180 – x
x + 38 = 180 – x
⇒ 2x = 180-38 = 142
x = \(\) = 71°
⇒ y = 180-71 = 109°

Question 72.
Write the number of solutions to 4x + 6y – 7 = 0 and 8x + 5y – 8 = 0.
Answer:
Only one solution.

Question 73.
Find the number of solutions to the pair of equation llx – 7y = 6 and 4x + 9y = 8.
Answer:
Only one solution.

Question 74.
\(\frac{2}{x}+\frac{3}{y}\) = 2, \(\frac{12}{x}-\frac{9}{y}\) = 3, then find ’x’.
Answer:
x = 2.

Question 75.
Write the pair of equations 4x – 2y + 6 = 0 and 2x – y + 8 = 0 has ……………. solutions.
Answer:
No solution.

Question 76.
Sita has pencils and pens which are together 40 in number. If she has 5 less pencils and 5 more pens the number of pens become four times the number of pencils. Represent this situation in a linear equation form.
Answer:
x + y = 40

Question 77.
Which type of equations
a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0 are …
Answer:
Pair of linear equations.

Question 78.
If ax + by = c and px + qy = r has unique solution, then write the condition.
Answer:
\(\frac{a}{b}=\frac{p}{q}\)

Question 79.
If the pair of equations kx + 14y + 8 = 0 and 3x + 7y + 6 = 0 has a unique so-lution, then find ’k’.
k ≠ 6

Question 80.
\(\frac{\mathbf{a x}}{\mathbf{b}}-\frac{\mathbf{b y}}{\mathbf{a}}\) = a + b, ax – by = 2ab, then find ‘x’.
Answer:
x = 3b

Question 81.
The pair of equations a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0 has a unique solution, then write the condition.
Answer:
\(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\)

Question 82.
Write the type of pair of lines
3x – 2y + 6 = 0, 6x – 4y + 8 = 0 are represents
Answer:
Parallel lines.

Question 83.
The age of a daughter is one third the age of her father. If the present age of father is ‘x’ years, then write the age of the daughter after 18 years in linear form.
Answer:
y = \(\frac{\mathrm{x}}{3}\) + 18

Question 84.
How many solutions \(\frac{\mathbf{a}_{1}}{\mathbf{a}_{\mathbf{2}}}=\frac{\mathbf{b}_{1}}{\mathbf{b}_{\mathbf{2}}}=\frac{\mathbf{c}_{1}}{\mathbf{c}_{\mathbf{2}}}\) will have ?
Answer:
Infinitely many solutions.

Question 85.
\(\frac{x+1}{2}+\frac{y-1}{3}=9, \frac{x-1}{3}+\frac{y+1}{2}=8\) then find x’.
Answer:
x = 13.

Question 86.
If the pair of equations 2x + y = 7 and 6x – py – 21 = 0 has infinite number of solutions, then find p.
Answer:
p = – 3
Explanation:
Infinite solutions,
so \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \Rightarrow \frac{2}{6}=\frac{1}{-p}\)
⇒ \(\frac{1}{3}=\frac{-1}{\mathrm{p}}\)
⇒ p = – 3

Question 87.
The ratio of incomes of two persons is 11:7 and the ratio of their expendi-tures is 9 : 5. If each of them manages to save ₹400 per month, then find the monthly income of first person.
Answer:
₹ 2200
Explanation:
11x – 9y = 400 and 7x – 5y = 400
On solving these equations income of first person was ₹ 2200.

Question 88.
Where the two lines 2x – y = 1, x + 2y = 13 will intersect each other ?
Answer:
(3,5)

Question 89.
Find the lines x – y = 1; 2x + y = 8 where they intersects at each other ?
Answer:
(3,2)
Explanation:
x = y + 1, 2(y + 1) + y = 8
⇒ 2y + 2 + y = 8
⇒ 3y = 6 ⇒ y = 2
⇒ x – 2 = 1 ⇒ x = 3

Question 90.
Write a line parallel to the line x + 2y + 1 = 0.
Answer:
2x + 4y + 1 = 0

Question 91.
If the equations (2m – l)x + 3y-5=0, 3x + (n – 1 )y – 2 — 0 has infinite number of solutions, then find ‘n’.
Answer:
n = \(\frac{11}{5}\).

Question 92.
Find where the line 2x + y = 7 inter-sects X – axis ?
Answer:
(\(\frac{7}{2}\), 0)

Question 93.
If \(\frac{5}{x-1}+\frac{1}{y-2}=2, \frac{6}{x-1}+\frac{-3}{y-2}=1\) then find ‘x’.
Answer:
x = 4

Question 94.
For what value of It, 2x + 3y = 4 and (k + 2)x + 6y = 3k + 2 will have infi-nitely many solutions ?
Answer:
k = 2
Explanation:
Infinitely many solutions, so

k + 2 = 4
k = 4 – 2 = 2

Question 95.
A fraction becomes \(\frac { 9 }{ 11 }\) if ‘2’ is added to both numerator and denominator. If ‘3’ is added to both numerator and denominator it becomes \(\frac { 5 }{ 6 }\), then find
the fraction.
Answer:
\(\frac { 7 }{ 9 }\) = fraction.
Explanation:
\(\frac{x+2}{y+2}=\frac{9}{11}\)
⇒ 11x + 22 = 9y + 18
⇒ 11 x – 9y = -4
\(\frac{x+3}{y+3}=\frac{5}{6}\)
⇒ 6x + 18 = 5y + 15
⇒ 6x – 5y = – 3
On solving these equations x = 7 and y = 9
∴ Fraction = \(\frac{x}{y}=\frac{7}{9}\)

Question 96.
Find the value of It’ for which the sys-tem of equations kx + 3y = 1, 12x + ky = 2 has no solution.
Answer:
k = – 6

Question 97.
The age of a father 8 years ago was 5 times that of his son 8 years. Hence, his age will be 8 years more than twice the age of his son. Then find the present age of father.
Answer:
48 years.

Question 98.
In the above problem, find the age of son.
Answer:
16 years.

Question 99.
If ad ≠ be, then find the pair of linear equations ax + by = p and cx + dy =q has how many solutions ?
Answer:
2 solutions.

Choose the correct answer satisfying the following statements.

Question 100.
Statement (A): Pair of linear equations 9x + 3y 4- 12 = 0, 18x 4- 6y + 24 = 0 have infinitely many solutions.
Statement (B): Pair of linear equations a₁x + b₁y + c₁ = 0 , a₂x + b₂y + c₂ = 0 have infinitely many solutions, if
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Explanation:
From the given equations, we have

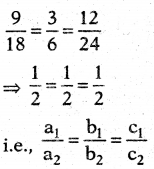
So, both A and B are correct and B explains A. Hence, (i) is the correct option.

Question 101.
Statement (A) : For k = 6, the system of linear equations x + 2y + 3 = 0 and 3x + ky + 6 = 0 is inconsistent. Statement (B) : The system of linear equations a₁x + b₁y + c₁ = 0,
a₂x + b₂y + c₂ = 0 is inconsistent if \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(ii)
Explanation:
For inconsistent solution we have bs
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
So, A is correct but B is incorrect.
Hence, (ii) is the correct option.

Question 102.
Statement (A): The value of q = ±2, if x = 3, y = 1 is the solution of the line 2x + y – q² – 3 = 0.
Statement (B): The solution of the line will satisfy the equation of the line.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Explanation:
As x = 3, y = 1 is the solution of
2x + y – q² – 3 = 0
⇒ 2 x 3 + 1 – q² – 3 = 0
⇒ 4 – q² = 0 ⇒ q² = 4 ⇒ q = ±2
So, both A and B are correct and B explains A.
Hence, (i) is the correct option.

Question 103.
Statement (A): The value of k for which the system of equations kx – y = 2, 6x – 2y = 3 has a unique solution is 3.
Statement (B) : The system of linear equations a₁x + b₁y + c₁ = 0,
a₂x + b₂y + c₂ = 0 has a unique solution if \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\)
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(iii)
Explanation:
Given system of linear equations has a
unique solution, if \(\frac{\mathrm{k}}{6} \neq \frac{1}{2}\)
⇒ \(\frac{\mathrm{k}}{6} \neq \frac{1}{2}\) ⇒ k ≠ 3
So, A is incorrect and B is corrrect.
Hence, (iii) is the correct option.

Question 104.
Statement (A) : The lines 2x – 5y = 7 and 6x – 15y = 8 are parallel lines.
Statement (B) : The system of linear equations a₁x + b₁y + c₁ = 0, a₂x + b₂y + c₂ = 0 have infinitely many
solutions if \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\).
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Explanation:
Two lines a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0 are parallel,
if \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
So, both A and B are correct.
Hence, (i) is the correct option.

Question 105.
Statement (A) : The system of equations 2x + y + 3 = 0 and 2x 4- y – 3=0 has no solution.
Statement (B) : The system of equations a₁x + b₁y + c₁ = 0, a₂x + b₂y + c₂ = 0 has a unique solution when \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\)
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)

Question 106.
Statement (A) : If the system of equations 2x + 3y = 7 and 2ax + (a + b)y = 28 has infinitely many solutions, then 2a – b = 0.
Statement (B) : The system of equations x – 5y = 3 and 2x- lOy = 5 has a unique solution.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(ii)

Question 107.
Statement (A): If the pair of lines are coincident, then we say that pair of lin-ear equations is consistent and it has a unique solution.
Statement (B) : If the pair of lines are parallel, then the pair of linear equations has no solution and is called inconsistent pair of equations.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(iii)

Question 108.
Statement (A) : 3x + 4y – 5 = 0 and 6x -I- ky + 9 = 0 represent parallel lines if k = 8.
Statement (B): a₁x + b₁y + c₁ = 0, a₂x + b₂y + c₂ = 0 represent parallel lines if \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Explanation:
In statement (A), given lines represent parallel lines, if
\(\frac{3}{6}=\frac{4}{\mathrm{k}} \neq \frac{5}{9} \Rightarrow \mathrm{k}=\frac{6 \times 4}{3}=8\)
∴ Statement (A) is true.
∴ Statement (B) is also true.
∴ Since reason is the correct explana¬tion for statement (A).
Option (i) is true.

Question 109.
Statement (A) : x + y – 4 = 0 and 2x + ky – 3 = 0 has no solution if k = 2.
Statement (B): a₁x + b₁y + c₁ = 0, a₂x + b₂y + c₂ = 0 are consistent if \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\)
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Explanation:
For (A), given equation has no solution, if
\(\frac{1}{2}=\frac{1}{\mathrm{k}} \neq \frac{-4}{-3}, \text { i.e., } \frac{4}{3}\)
⇒ k = 2 [ \(\frac{1}{2} \neq \frac{4}{3}\) holds]
∴ (A) is true.
Since (B) does not give result of (A), so option (i) is true.

Question 110.
Statement (A): If the system of equa-tions 2x + 3y = 7 and 2ax + (a + b)y = 28 has infinitely many solutions, then 2a – b = 0.
Statement (B) : The system of equations 3x – 5y = 9 and 6x- lOy = 8 has a unique solution. –
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(ii)
Explanation:
For (A), given system of equations has infinitely many solutions, if
\(\frac{2}{2 a}=\frac{3}{a+b}=\frac{-7}{-28}, \text { i.e., }\)
⇒ \(\frac{1}{a}=\frac{3}{a+b}=\frac{1}{4}\)
⇒ 3a = a + b ⇒ 2a – b = 0
Also clearly a = 4 and
a + b = 12 ⇒ b = 8
∴ 2a – b = 8 – 8 = 0
∴ (A) is true.
But (B) is false ∵ \(\frac{3}{6}=\frac{-5}{-10}\)
[∵ 3(-10) = (-5) (6) = -30]
For unique solution, if
\(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\)
∴ Option (ii) is true.

Question 111.
Statement (A): If kx – y – 2 = 0 and 6x – 2y – 3 = 0 are inconsistent, then k = 3.
Statement (B): a₁x + b₁y + c₁ = 0, a₂x + b₂y + c₂ = 0 are inconsistent if \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)
Explanation:
Statement (A) is true.

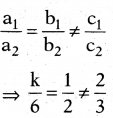
⇒ k = 3.
Statement (B) is also true.
∴ Option (i) is true.

Question 112.
Statement (A): 3x – 4y = 7 and
6x – 8y = k have infinite number of solutions if k = 14.
Statement (B): a₁x + b₁y + c₁ = 0, a₂x + b₂y + c₂ = 0 have a unique solution if \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\)
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i)

Question 113.
Statement (A) : The linear equations x – 2y – 3 = 0 and 3x + 4y – 20 = 0 have exactly one solution.
Statement (B) : The linear-equations 2x + 3y – 9 = 0 and 4x + 6y – 18 = 0 have a unique solution.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(ii)

Question 114.
Statement (A) : kx + 2y = 5 and 3x + y = 1 have a unique solution if
k = 6.
Statement (B) : x + 2y = 3 and 5x + ky + 7 = 0 have a unique solution k ≠ 1.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(iv)

Read the below passages and answer to the following questions.

If we have two simultaneous equations ax + by = c and bx + ay — d, l (c + d c-d^
then x = \(\frac{1}{2}\left(\frac{\mathrm{c}+\mathrm{d}}{\mathrm{a}+\mathrm{b}}+\frac{\mathrm{c}-\mathrm{d}}{\mathrm{a}-\mathrm{b}}\right)\) and y = \(\frac{1}{2}\left(\frac{c+d}{a+b}-\frac{c-d}{a-b}\right)\)

Question 115.
Find the solution of 217x + 131y = 913 and 131x + 217y = 827.
Answer:
x = 3, y = 2
Explanation:
We have 217x + 131y = 913
131x + 217y = 827

Question 116.
Find the solution of 37x + 41y = 70 and 4lx + 37y = 86.
Answer:
x = 3, y = – 1
Explanation:
We have,
37x + 41y = 70
41x + 37y = 86

Question 117.
Find the solution of x + 2y = \(\frac { 3 }{ 2 }\) and 2x + y = \(\frac { 3 }{ 2 }\)
Answer:
x = \(\frac { 1 }{ 2 }\), y = \(\frac { 1 }{ 2 }\)
A system of linear equations is given as follows :
a₁x + b₁y + c₁ = 0 and
a₂x + b₂y + c₂ = 0
Explanation:
We have

Question 118.
Write the condition for two lines to have a unique solution.
Answer:
\(\frac{a_{1}}{a_{2}} \neq \frac{c_{1}}{c_{2}}\)

Question 119.
Write the condition for two lines to have infinitely many solutions.
Answer:
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)

Question 120.
Write the condition both lines are par-allel only.
Answer:
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
6 pencils and 4 notebooks together cost ₹ 90 whereas. 8 pencils and 3 notebooks together cost ₹ 85.

Question 121.
Create an equation to first situation.
Answer:
6x + 4y = 90.

Question 122.
Create an equation to second situation.
Answer:
8x + 3y = 85

Question 123.
Which mathematical concept is used to find the cost of notebook and pencil ?
Answer:
Pair of linear equations.
A boat goes 30 km upstream and 44 km downstream in 10 hrs. In 13 hrs it can go 40 km upstream and 55 km downstream.

Question 124.
Prepare an equation to first condition.
Answer:
\(\frac{30}{x-y}+\frac{44}{x+y}=10\)

Question 125.
Prepare an equation to second condition.
Answer:
\(\frac{40}{x-y}+\frac{55}{x+y}=13\)

Write the correct option to match the column -I and column – II, which gave value of ‘x1 and ‘y’ for pair of equation given in column -I.

Question 126.

Answer:
A – (iv), B – (ii)

Question 127.

A – (iii), B – (i)

Question 128.

A – (ii), B – (iv)

Question 129.

A – (i), B – (iii)

Answer Questions 130 and 131 based on the data given below.
“The cost of 1 kg potatoes and 2kg to-matoes was ₹ 30 on a certain day. After two days the cost of 2 kg potatoes and 4 kg tomatoes was found to be ₹ 66”.

Question 130.
Write a pair of linear equations in two variables x and y from the datAnswer:
Solution:
x + 2y = 30, 2x + 4y = 66 (or) x + 2y = 33

Question 131.
Which system of linear equations in two variables does the data represent ?
Answer:
Parallel lines, inconsistent, no solution.

Question 132.
For what value of ‘k’ is the pair of linear equations x + 2y = 7 and3x – ky = 21 has infinitely many solutions ?
Answer:
Given equations are x + 2y = 7 and 3x – ky = 21 has infinitely many solutions, so

Question 133.
What is the value of ‘x’ in 4x – 7y = 9 ify = 3?
Answer:
Given , 4x – 7y = 9
If y = 3, then 4x – 7(3) = 9
=> 4x-21 = 9
=> 4x = 30
x = \(\frac{30}{4}=\frac{15}{2}\)

Question 134.
Lahari bought two pens and five pencils spending Rs. 30. Express this information as a linear equation in variables x and y.
Answer:
Let the cost of each pen be ₹ x and the cost of each pencil be ₹ y.
By problem, 2x + 5y = 30