These AP 10th Class Maths Chapter Wise Important Questions 2nd Lesson సమితులు will help students prepare well for the exams.
AP Board 10th Class Maths 2nd Lesson Important Questions and Answers సమితులు
ప్రశ్న 1.
A = {1, 2, 3, 4} ను సమితి నిర్మాణం రూపంలో వ్రాయండి.
సాధన.
దత్త సమితి A = {1, 2, 3, 4}
దీనిని సమితి నిర్మాణ రూపంలో వ్రాయగా –
A = {x/ x ∈ N, x < 5}
ప్రశ్న 2.
’42’ ను భాగించగల అన్ని సహజ సంఖ్యల సమితిని రోస్టర్ మరియు సమితి నిర్మాణ రూపంలో వ్రాయండి.
సాధన.
42 ను భాగించు అన్ని సహజ సంఖ్యలు అనగా
42 యొక్క కారణాంకాలు అగును. అవి 1, 2, 3, 6, 7, 14, 21, 42 … రోస్టర్ రూపం = {1, 2, 3, 6, 7, 14, 21, 42} సమితి నిర్మాణరూపం = {x/x ∈ N, x అనేది 42 యొక్క కారణాంకం}.
![]()
ప్రశ్న 3.
B = {p, q} సమితికి గల ఉప సమితులు అన్నింటిని వ్రాయండి.
సాధన.
{p}, {q}, {p, q}, { } ఈ నాలుగు సమితులు
B = {p, q} కు ఉప సమితులు.
n(B) = 2 కావున B యొక్క ఉప సమితుల సంఖ్య = 2n = 22 = 4
ప్రశ్న 4.
{x: x = 2n + 1 మరియు n E N} ను రోస్టరు రూపంలో వ్రాయండి.
సాధన.
n ∈ N అయిన n = 1, 2, 3, …… అగును.
n = 1 అయిన x = 2n + 1 = 2(1) + 1 = 2 + 1 = 3 మరియు
n = 2 అయిన X = 2n + 1 = 2(2) + 1 = 4 + 1 = 5 మరియు
n = 3 అయిన x = 2n + 1 = 2(3) + 1 = 6 + 1 = 7
కావున {3, 5, 7, 9, …..} అనునది పై సమితి యొక్క రోస్టరు రూపం అగును.
![]()
ప్రశ్న 5.
A = {10 కంటే తక్కువైన ప్రధానాంకాలు}, . B = {10 కంటే తక్కువైన ధన బేసి సంఖ్యలు}, అయితే (i) An B (ii) B – A లను కనుగొనుము.
సాధన.
A = {10 కంటే తక్కువైన ప్రధానాంకాలు},
B = {10 కంటే తక్కువైన ధన బేసి సంఖ్యలు
∴ A = {2, 3, 5, 7} మరియు
B = {1, 3, 5, 7, 9}
(i) (A ∩ B) = {2, 3, 5, 7} ∩ {1, 3, 5, 7, 9} = {3, 5, 7} …………….. (1) మరియు
(ii) B – A = {1, 3, 5, 7, 9} – {2, 3, 5, 7}
(B – A) = {1, 9} – (2)
ప్రశ్న 6.
A = {\(\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}, \frac{1}{32}\)} అయిన సమితి A ను సమితి నిర్మాణరూపంలో వ్రాయుము.
సాధన.
A = {\(\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}, \frac{1}{32}\)}
A = {x : x = \(\frac{1}{v}\) y = 2n. n ∈ N, n ≤ 5} (లేదా)
A = {x : x = \(\frac{1}{2^{n}}\) n ∈ N, n ≤ 5}
ప్రశ్న 7.
A = {3, 9, 27, 81}ను సమితి నిర్మాణ రూపంలో రాయండి.
సాధన.
A = {x : x = 3n, n < 5, n ∈ N} లేదా
A = {x : x = 3n, n ≤ 5, n ∈ N}.
![]()
ప్రశ్న 8.
A = {\(1, \frac{1}{4}, \frac{1}{9}, \frac{1}{16}, \frac{1}{25}\)} ను సమితి నిర్మాణ రూపంలో వ్రాయుము.
సాధన.
\(\frac{1}{1}, \frac{1}{4}, \frac{1}{9}, \frac{1}{16}, \frac{1}{25}\) అనునవి \(\frac{1}{p^{2}}\) రూపంలో ఉన్నవి. p విలువ 6 కంటే తక్కువగా ఉన్నది. కావున
A = {x : x = \(\frac{1}{p^{2}}\), p ∈ N, p < 6} అనునది A యొక్క నిర్మాణ రూపం.
ప్రశ్న 9.
A = {2, 4, 8, 16} ను సమితి నిర్మాణ రూపంలో రాయండి.
సాధన.
A = {2n/n ∈ N మరియు n < 5}
ప్రశ్న 10.
A = {x : x అనేది 10 కంటే తక్కువైన సరి సంఖ్య }
B = {x : x అనేది 10 కంటే తక్కువైన ప్రధాన సంఖ్య } అయితే A ∩ B ను కనుగొనుము.
సాధన.
దత్తాంశము A = {x : x అనేది 10 కంటే తక్కువైన సరి సంఖ్య}
A = {2, 4, 6, 8} మరియు B = {x : x అనేది 10 కంటే తక్కువై న్రధాన సంఖ్య}
∴ B = {2, 3, 5, 7}
A ∩ B = {2, 4, 6, 8} n {2, 3, 5, 7}
∴ A ∩ B = {2}
![]()
ప్రశ్న 11.
సమితి A, సమితి B కు ఉపసమితి. n(A) = 4 మరియు n(B) = 7 అయిన n(A U B) కనుగొనుము.
సాధన.
A ⊂ B; n(A) = 4 మరియు n(B) = 7 n(A U B) = 7
ప్రశ్న 12.
(i) A U B = B,
(ii) A ∩ B = B.
అగు విధంగా A, B సమితులకు ప్రతీ ప్రశ్నకు ఒక్కొక్క ఉదాహరణ ఇవ్వండి.
సాధన.
(i) A = {1, 2, 3}, B = {1, 2, 3, 4, 5} అనుకొనుము.
A U B = {1, 2, 3} U {1, 2, 3, 4, 5}
= {1, 2, 3, 4, 5} = B
∴ A U B = B
(ii) A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ……}, B = {2, 4, 6, 8, 10, …..} అనుకొనుము.
A ∩ B= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ….} ∩ {2, 4, 6, 8, 10, …..}
= {2, 4, 6, 8, 10, …..} = B
∴ A ∩ B = B.
![]()
ప్రశ్న 13.
క్రింది వెన్ చిత్రాన్ని పరిశీలించి, దిగువ ప్రశ్నలకు జవాబులు రాయండి.
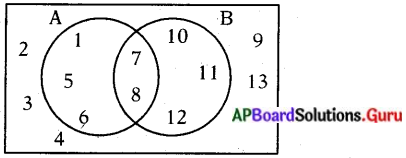
(i) A U B
(ii) A – B లను కనుగొనండి.
సాధన.
(i) A U B = {1, 5, 6, 7, 8, 10, 11, 12}
(ii) A – B = {1, 5, 6}
ప్రశ్న 14.
A = {5, 6, 7}, B = {6, 7, 8, 9} అయిన A – (A – B) మరియు A ∩ B కనుగొనుము. ఏమి గమనించితివి ?
సాధన.
A = {5, 6, 7}, B = {6, 7, 8, 9}
A – B = {5, 6, 7} – {6, 7, 8, 9} = {5, 6, 7, 8, 9} = {5}
A = (A – B) = {5, 6, 7} – {5} = {6, 7}
A ∩ B = {5, 6, 7} ∩ {6, 7, 8, 9} = {6, 7}
A – (A – B) = A ∩ B అని గమనించితిని.
![]()
ప్రశ్న 15.
A = {x : x ఒక సరి సంఖ్య}, B = {x : x ఒక బేసి సంఖ్య}, C = {x : x ఒక ప్రధాన సంఖ్య } D = {x : x, 5 యొక్క గుణకం} అయిన
(i) A U B,
(ii) A ∩ B
(iii) C – D
(iv) A ∩ C లను కనుగొనుము.
సాధన.
A = {x : x ఒక సరి సంఖ్య } అనగా A = {2, 4, 6, 8, …… }
B = {x : x ఒక బేసి సంఖ్య} అనగా B = {1, 3, 5, 7, …… }
C = {x : x ఒక ప్రధాన సంఖ్య } అనగా C = {2, 3, 5, 7, 11, …. }
D = {x : x, 5 యొక్క గుణకం} అనగా D = {5, 10, 15, 20, ….. }
(i) A U B = {2, 4, 6, 8, ….} U {1, 3, 5, 7, 9, …. } = {1, 2, 3, 4, 5, …..} అనగా సహజ సంఖ్యా సమితి అగును.
(ii) A ∩ B = {2, 4, 6, 8, ….} ∩ {1, 3, 5, 7, 9, …. } = { } అనగా ఇది శూన్య సమితి అగును.
(iii) C – D = {2, 3, 5, 7, 11, ….} – {5, 10, 15, 20, ……} = {2, 3, 7, 11, …..} అనగా 5 లేని ప్రధాన సంఖ్యల సమితి
(iv) A ∩ C = {2, 4, 6, 8, 10, ….} ౧12, 3, 5, 7, 11, …. } = { 2 } అనగా సరి ప్రధానసంఖ్య.
![]()
ప్రశ్న 16.
A = {1, 2, 3, 4}, B = {1, 2, 3, 5, 6} అయిన
(i) A ∩ B
(ii) B ∩ A
(iii) A – B
(iv) B – A లను కనుగొని వాటి నుంచి నీవేమి గమనించితివో వ్యాఖ్యానించుము.
సాధన.
(i) A = {1, 2, 3, 4} మరియు B = {1, 2, 3, 5, 6}
A ∩ B = {1, 2, 3, 4} 9 {1, 2, 3, 5, 6} = {1, 2, 3}
∴ A ∩ B = {1, 2, 3} ……………… (1)
(ii) A = {1, 2, 3, 4} మరియు B = {1, 2, 3, 5, 6}
B ∩ A = {1, 2, 3, 5, 6} ∩ {1, 2, 3, 4} = {1, 2, 3} కావున
∴ B ∩ A = {1, 2, 3} …………….. (2)
∴ A ∩ B = B ∩ A అయినది..
(iii) A = {1, 2, 3, 4} మరియు B = {1, 2, 3, 5, 6} అయిన
A – B = {1, 2, 3, 4} – {1, 2, 3, 5, 6} = {4}
కావున A – B = {4}
(iv) B = {1, 2, 3, 5, 6} మరియు A = {1, 2, 3, 4} అయిన
B – A = { 1, 2, 3, 5, 6} – {1, 2, 3, 4} = {5, 6}
∴ B – A = {5, 6}
కావున A – B ≠ B – A అని గమనించవచ్చు.
![]()
ప్రశ్న 17.
A = {3, 6, 9, 12, 15, 18, 21}, B = {4, 8, 12, 16, 20} అయిన A U B = B U A మరియు A – B = B – A అవుతుందా ? సరిచూడుము.
సాధన.
A U B = {3, 6, 9, 12, 15, 18, 21} U {4, 8, 12, 16, 20} = {3, 4, 6, 8, 9, 12, 15, 16, 18, 20, 21}
B U A = {4, 8, 12, 15, 16, 20} U {3, 6, 9, 12, 15, 18, 21} = {3, 4, 6, 8, 9, 12, 15, 16, 18, 20, 21}
∴ A U B = B U A
A – B = {3, 6, 9, 12, 15, 18, 21} – {4, 8, 12, 16, 20} = {3, 6, 9, 15, 18, 21}
B – A = {4, 8, 12, 16, 20} – {3, 6, 9, 12, 15, 18, 21} = {4, 8, 16, 20}
A – B ≠ B – A
ప్రశ్న 18.
A = {x: x ఒక సరి సహజ సంఖ్య మరియు x < 12} మరియు B = {x : x ఒక సహజ సంఖ్య మరియు 6ను – భాగిస్తుంది} అయిన,
(i) (A U B) – (A ∩ B),
(ii) (A – B) U (B – A) లను కనుగొనుము. ఫలితం నుండి మీరు ఏమి గమనించారు ?
సాధన.
A = {2, 4, 6, 8, 10}; B = {1, 2, 3, 6}
A U B = {2, 4, 6, 8, 10} U {1, 2, 3, 6} = {1, 2, 3, 4, 6, 8, 10}
A ∩ B = {2, 4, 6, 8 10} ∩ {1, 2, 3, 6} = {2, 6}
(A U B) – (A ∩ B) = { 1, 2, 3, 4, 6, 6, 10} – {2, 6} = {1, 3, 4, 8, 10}
A – B = {2, 4, 6, 8, 10} – {1, 2, 3, 6} = {4, 8, 10}
B – A = {1, 2, 3, 6} {2, 4, 6, 8, 10} = {1, 3}
(A – B) U (B – A) = {4, 6, 10} U {1, 3} = {1, 3, 4, 8, 10}
(A U B) – (A ∩ B) = (A – B) U (B A) అని గమనించితిని.
![]()
ప్రశ్న 19.
A = {x : x ఒక సహజ సంఖ్య}, B = {x : x ఒక సరి సహజ సంఖ్య}, C = {x : x ఒక బేసి సహజ సంఖ్య}, D = {x : x ఒక ప్రధాన సంఖ్య}, అయిన A U B, A ∩ C, B ∩ C, B ∩ D లను కనుగొనండి. మీరు ఏమి గమనించారు ?
సాధన.
A = {x : x ఒక సహజ సంఖ్య} = {1, 2, 3, …. }
B = {x : x ఒక సరి సహజ సంఖ్య} = {2, 4, 6, …… }
C = {x : x ఒక బేసి సహజ సంఖ్య} = {1, 3, 5, …….}
D = {x : x ఒక ప్రధానాంకము} . = {2, 3, 5, …….. }
A U B = {1, 2, 3, ….} U {2, 4, 6, …. } = {1, 2, 3, …….}
A ∩ C = {1, 2, 3, ….} ∩ {1, 3, 5, …. } = {1, 3, 5, ……}
B ∩ C = {2, 4, 6, ….} ∩ {1, 3, 5, …. } = { } = Φ
B ∩ D = {2, 4, 6, ….} ∩ {2, 3, 5, …. } = { 2 }
A U B = A; A ∩ C = C.
ప్రశ్న 20.
A = {x : x ఒక ప్రధాన సంఖ్య మరియు x < 20} మరియు B = {x : x = 2x + 1, x ∈ W మరియు x < 9), అయిన
(i) A ∩ B
(ii) B ∩ A
(iii) A – B
(iv) B – A లను కనుగొనుము. నీవు ఏమి గమనించావు ?
సాధన.
A = {2, 3, 5, 7, 11, 13, 17, 19}
B = {1, 3, 5, 7}
(i) A ∩ B= {2, 3, 5, 7, 11, 13, 17, 19} ∩ {1, 3, 5, 7} = {3, 5, 7}
(ii) B ∩ A = {1, 3, 5, 7} – {2, 3, 5, 7, 11, 13, 17, 19} = {3, 5, 7}
(iii) A – B = {2, 3, 5, 7, 11, 13, 17, 19} – {1, 3, 5, 7} = {2, 11, 13, 17, 19}
(iv) B – A = {1, 3, 5, 7} – {2, 3, 5, 7, 11, 13, 17, 19}
= {1}
∴ A ∩ B = B ∩ A
A – B ≠ B – A అని గమనించితిని.
![]()
ప్రశ్న 21.
A = {x : x, 6 కన్నా తక్కువైన ఒక సహజ సంఖ్య}, B = {x : x, 60 ను భాగించు ఒక ప్రధాన సంఖ్య} C = {x : x, 10 కంటే తక్కువైన ఒక బేసి సహజ సంఖ్య} D = {x : x, 48 ను భాగించు ఒక సరి సహజ సంఖ్య} అయిన వీటికి రోస్టర్ రూపం రాసి
(i) A U B
(ii) B ∩ C
(iii) A – D
(iv) D – B లను కనుక్కోండి.
సాధన.
A = {1, 2, 3, 4, 5}; B = {2, 3, 5} C = {1, 3, 5, 7, 9}; D = {2, 4, 6, 8, 12, 16, 24, 48}
(i) A U B = {1, 2, 3, 4, 5} U {2, 3, 5} = {1, 2, 3, 4, 5}
(ii) B ∩ C = {2, 3, 5} 0 {1, 3, 5, 7, 9) = {3, 5}
(iii) A – D = {1, 2, 3, 4, 5} -{2, 4, 6, 8, 12, 16, 24, 48} = {1, 3, 5}
(iv) D – B = {2, 4, 6, 8, 12, 16, 24, 48} – {2, 3, 5} = {4, 6, 8, 12, 16, 24, 48}
ప్రశ్న 22.
A = {x/x ∈ W, x < 10}, B = {x/x అనేది 10 యొక్క కారణాంకం} C = {12, 22, 33, ……… 102} లు మూడు సమితులు అయితే
(i) A U B
(ii) A ∩ B
(iii) A – C
(iv) B – Cలు కనుగొనుము.
సాధన.
A = {x/x ∈ W x < 101} B = {x/x అనేది 10 యొక కారణాంకం} C = {12, 22, 3, ……….. 102
కావున A = {0, 1, 2, 3, 4 5, 6, 7, 8, 9}
B = {1, 2, 5, 10}
C = {1, 4, 7, 16, 25, 36, 49, 64, 81, 100}
(i) A U B = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} U {1, 2, 5, 10} = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10} …………… (1)
(ii) A ∩ B = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} ∩ {1, 2, 5, 10} = {1, 2, 5} ……….. (2)
(iii) A – C = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} – {1, 4, 9, 16, 25, 36, 49, 64, 81, 100} = {0, 2, 3, 5, 6, 7, 8} ………………. (3)
(iv) B – C = { 1, 2, 5, 10} – {1, 4, 9, 16, 25, 36, 49, 64, 81, 100} = {2, 5, 10} ………… (4)
![]()
ప్రశ్న 23.
A = {- 2, 1, 3, 4, 5}, B = {7, 3, 5, 2, 8} మరియు C = {- 2, 4, 5, 8, 9} అయిన క్రింది సమితులను కనుగొనుము.
(i) A – (B U C),
(ii) (A – B) ∩ (A – C) ఏమి గమనించితివి ?
సాధన.
A = {-2, 1, 3, 4, 5}; B = {7, 3, 5, 2, 8}, C = {- 2, 4, 5, 8, 9}
(i) A – (B U C)
B U C = {7, 3, 5, 2, 8} U {- 2, 4, 5, 8, 9} = {- 2, 2, 3, 4, 5, 7, 8, 9}
A – (B U C) = {- 2, 1, 3, 4, 5} – {- 2, 2, 3, 4, 5, 7, 8, 9} = {1}
(ii) (A – B) ∩ (A – C)
A – B = {- 2, 1, 3, 4, 5} – {7, 3, 5, 2, 8} = {- 2, 1, 4}
A – C = {-2, 1, 3, 4, 5} – {- 2, 4, 5,8, 9} = {1, 3}
(A – B) ∩ (A – C) = {- 2, 1,4 } ∩ {1, 3} = {1}
A – (B U C) = (A – B) ∩ (A – C)
ప్రశ్న 24.
A = {క్రమ బహుభుజులు}, B = {త్రిభుజములు} మరియు C = {చతుర్భుజములు}. అయిన ,
(i) A ∩ B
(ii) A ∩ c
(iii) A – B
(iv) A – C లను కనుగొనుము.
సాధన.
A = {త్రిభుజాలు, చతుర్భుజాలు, పంచభుజులు, షడ్భుజులు, సప్తభుజులు} B = {త్రిభుజములు}; C = {చతుర్భుజములు}
(i) A ∩ B = {త్రిభుజాలు, చతుర్భుజాలు, పంచభుజులు, షడ్భుజులు, సప్తభుజులు} ∩ {త్రిభుజములు} = {త్రిభుజములు}
(ii) A ∩ C = {త్రిభుజాలు, చతుర్భుజాలు, పంచభుజులు, షడ్భుజులు, సప్త భుజులు} ∩ {చతుర్భుజములు}= {చతుర్భుజములు}
(iii) A – B = {త్రిభుజాలు, చతుర్భుజాలు, పంచభుజులు, షడ్భుజులు, సప్తభుజులు} – {త్రిభుజములు | = {చతుర్భుజాలు, పంచభుజులు, షడ్భుజులు, సప్త భుజులు}
(iv) A – C = {త్రిభుజాలు, చతుర్భుజాలు, పంచభుజులు, షడ్భుజులు. సప్తభుజులు} – {చతుర్భుజములు} = {త్రిభుజాలు, పంచభుజులు, షడ్భుజులు, సప్తభుజులు}