AP 7th Class Maths Notes 8th Lesson ఘాతాంకాలు మరియు ఘాతాలు

Students can go through AP Board 7th Class Maths Notes 8th Lesson ఘాతాంకాలు మరియు ఘాతాలు to understand and remember the concept easily.

AP Board 7th Class Maths Notes 8th Lesson ఘాతాంకాలు మరియు ఘాతాలు

→ పెద్ద సంఖ్యలను సరళమైన రీతిలో చదవడం, రాయడం, అర్థం చేసుకోవటంలో ఘాతాంకాలు దోహదపడతాయి.
ఉదా : 2 × 2 × 2 × 2 × 2 × 2 = 26
a × a × a … ‘n’ సార్లు = aⁿ

→ ఘాతాంక న్యాయాలు :
‘n’ మరియు ‘m’ లు ఏవైనా రెండు శూన్యేతర పూర్ణసంఖ్యలు, ‘a’ మరియు ‘b’ లు పూర్ణసంఖ్యలైన ,

• a^m × aⁿ = a^m+n
• (a^m)ⁿ = a^mn

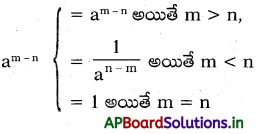
• a^m × b^m = (ab)^m
• a^m ÷ b^m = \(\left(\frac{a}{b}\right)^{m}\)
• a⁰ = 1 (where a ≠ 0)
• (-1)^{సరిసంఖ్య} = 1
• (-1 )^{బేసిసంఖ్య} = -1

→ ఒక సంఖ్యను 1 నుండి 9 మధ్యగల దశాంశ భిన్నంగా మరియు 10 యొక్క ఘాతాలతో లబ్దం చేయటాన్ని ప్రామాణిక రూపంలో వ్యక్తపరచడం అంటాం.

→ ఘాతరూపం : ఒక సంఖ్య యొక్క పునరావృత గుణకారాన్ని సరళమైన రీతిలో వ్యక్తపరచడాన్ని ఘాతరూపం
అంటారు.
ఉదా : 2 × 2 × 2 = 2³
10 × 10 × 10 × 10 = 10⁴
10⁴ లో 10ని భూమి అని, 4 ను ఘాతాంకం అని అంటారు.

→ ఘాతాంక సాధారణ రూపం : a × a × a × ……. n సార్లు = aⁿ ను ఘాతాంక సాధారణ రూపం అని
అంటారు. ఇక్కడ a భూమి, n ఘాతాంకం.

→ ప్రామాణిక రూపం : ఒక సంఖ్యను 1 నుండి 9 వరకు గల దశాంశ భిన్నం మరియు 10 యొక్క పూర్ణాంక ఘాతాల లబ్దంగా వ్రాయుటను ప్రామాణిక రూపంలో వ్యక్తపరచడం అంటాం.
ఉదా : 59 = 5.9 × 10
590 = 5.9 × 10²
5904 = 5.904 × 10³