SCERT AP 10th Class Maths Textbook Solutions Chapter 13 సంభావ్యత InText Questions Textbook Exercise Questions and Answers.
AP State Syllabus 10th Class Maths Solutions 13th Lesson సంభావ్యత InText Questions
ఇవి చేయండి:
అ. క్రింది ఘటనలలో దేని పర్యవసానములన్నీ సమ సంభవాలు? (పేజీ నెం.. 307)
ప్రశ్న 1.
పాచిక (dies) ను ఎగురవేసినపుడు 1, 2, 3, 4, 5 లేక 6 పడుట.
సాధన.
ఒక పాచికను వేసిన దాని పై ముఖంపై 1, 2, 3, 4, 5 లేదా 6 సంఖ్యలు వచ్చుటకు (ఒక్కొక్కదానికి) సమాన అవకాశాలు కలవు.
ప్రశ్న 2.
5 ఎరుపు, 4 నీలం, 1 నలుపు బంతులు గల సంచి నుండి ఒక బంతిని యాదృచ్చికంగా తీయుట.
సాధన.
5 ఎరుపు బంతులు, 4 నీలం బంతులు, 1 నల్లని బంతి గల సంచి నుండి 2 వేర్వేరు రంగులు కల బంతులను బయటకు తీయుటకు (పొందుటకు) సమాన అవకాశాలు లేవు.
ప్రశ్న 3.
కారమ్స్ ఆటను గెలుచుట.
సాధన.
క్యారమ్స్ ఆట గెలుచుటకు ఇద్దరికీ సమాన అవకాశాలు , కలవు.
![]()
ప్రశ్న 4.
రెండంకెల సంఖ్యలో ఒకట్ల స్థానము 0, 1, 2, 3, 4, 5, 6, 7, 8 లేక 9 అగుట.
సాధన.
0, 1, 2, 3, 4, 5, 6, 7, 8 లేదా 9 నుండి రెండంకెల సంఖ్యను వ్రాయుటలో ఒకట్ల స్థానంలో పై అంకెలు వచ్చుటకు సమాన అవకాశాలు కలవు.
ప్రశ్న 5.
10 ఎరుపు, 10 నీలం, 10 నలుపు రంగు బంతులు గల సంచి నుండి ఒక బంతిని యాదృచ్చికంగా తీయుట.
సాధన.
10 ఎరుపు, 10 నీలం, 10 నలుపు బంతులు గల సంచి నుండి వేర్వేరు రంగులు గల బంతులు బయటకు తీయుటకు (పొందుటకు) సమాన అవకాశాలు కలవు.
ప్రశ్న 6.
జూలై నెలలో ఒక రోజు వర్షం రావడం.
సాధన.
జూలై నెలలో ఒక కచ్చితమైన రోజున వర్షం పడుటకు సమాన అవకాశాలు కలవు.
ఆ. పై అన్ని ఘటనల యొక్క పర్యవసానాలన్నీ సమ సంభవాలేనా?
సాధన.
అన్ని ఘటనల ఫలితాలు సమాన అవకాశాలను కలిగి ఉండవు.
![]()
ఇ. పర్యవసానాలన్నీ సమసంభవాలైన 5 ఘటనలను, సమసంభవాలు కాని 5 ఘటనలను పేర్కొనండి.
సాధన.
సమాన అవకాశాలు గల ఘటనలు : –
ఎ) ఒక పాచికను వేసిన సరి లేదా బేసిసంఖ్యను పొందే ఘటనలు.
బి) ఒక నాణేన్ని ఎగురవేసిన బొమ్మ లేదా బొరుసు పొందే ఘటనలు.
సి) 1 నుండి 10 వరకు సంఖ్యలు రాసిన కార్డుల నుండి సరి లేదా బేసిసంఖ్య గల పేక పొందే ఘటనలు.
డి) 8 ఆకుపచ్చ మరియు 8 నల్లని ,బంతులు గల సంచి నుండి ఆకుపచ్చ లేదా నల్లని బంతిని తీయగల ఘటనలు.
ఇ) 20 మంది బాలురు మరియు 20 మంది బాలికలు గల ఒక తరగతి నుండి ఒక బాలుడు లేదా బాలికను ఎన్నుకొను ఘటనలు.
ఎఫ్) పేకముక్కల కట్ట నుండి ఎరుపు లేదా నలుపు రంగు కార్డును ఎన్నుకోగల ఘటనలు.
సమాన అవకాశాలు లేని ఘటనలు :
ఎ) ఒక పాచికను విసిరిన దానిపై “ప్రధాన” లేదా “సంయుక్త” సంఖ్యను పొందే ఘటనలు.
బి) 1 నుండి 5 సంఖ్యలు గల పేకముక్కల నుండి సరి లేదా బేసి సంఖ్య గల పేకను పొందే ఘటనలు.
సి) 1, 2, ….. 10 సంఖ్యలలో 3 యొక్క గుణిజం లేదా 3 యొక్క గుణిజం కాని సంఖ్యను ఎన్నుకొనే ఘటనలు.
డి) ఒక పాచికను దొర్లించినపుడు 5 కంటే తక్కువైన (చిన్నదైన) సంఖ్య లేదా 5 కంటే పెద్దదైన సంఖ్యను పొందే ఘటనలు.
ఇ) 5 ఆకుపచ్చ మరియు 8 తెలుపు బంతుల నుండి ఒక తెలుపు లేదా ఆకుపచ్చ బంతిని పొందగల (తీయగల) ఘటనలు.
![]()
ప్రశ్న 7.
సమసంభవ పర్యవసానములు గల ఐదు సందర్భాలను పేర్కొని వాని ప్రతిరూప ఆవరణలను వ్రాయండి. . , సమసంభవము మరియు పరస్పర వర్ణిత ఘటనల యొక్క సంభావ్యతను ఎట్లు గమనించవచ్చునో కొన్ని ఉదాహరణలను పరిశీలిద్దాము . (పేజీ.నెం.309)
సాధన.
a) ఒక నాణేన్ని పైకి ఎగురవేసిన బొమ్మ లేదా బొరుసు పొందే సందర్భం.
∴ ప్రతిరూప ఆవరణము S = {T, H}
b) ఒక పాచికను దొర్లించినపుడు సరి లేదా బేసి సంఖ్యను పొందటం.
∴ ప్రతిరూప ఆవరణము S = {1, 2, 3, 4, 5, 6}.
c) షటిల్ ఆటను గెలిచే సందర్భం .
∴ ప్రతిరూప ఆవరణం S = {గెలుపు, ఓటమి}.
d) 3 నీలం మరియు 3 నల్లని బంతులు గల సంచి నుండి ఒక నలుపు లేదా నీలం బంతిని . యాదృచ్చికంగా తీసే సందర్భం.
∴ ప్రతిరూప ఆవరణం S = {నీలం, నల్లని బంతులు}.
e) పేక ముక్కల కట్ట నుండి 1 నలుపు లేదా 1 ఎరుపు పేక ముక్కను యాదృచ్ఛికంగా తీసే సందర్భం
∴ ప్రతిరూప ఆవరణం S = {నలుపు, ఎరుపు}
![]()
ప్రశ్న 8.
(i) బొమ్మ పడుట అనేది బొరుసు పడుటకు పూరక ఘటనా? – కారణాలు తెలపండి. (పేజీ.నెం.311)
సాధన.
ఒక నాణెమును ఎగురవేసినపుడు సాధ్యమగు పర్యవసానాల సమితి S = {T, H}
బొమ్మపడు ఘటన కాకుండా Sలో మిగిలిన ఘటన పర్యవసానం బొరుసు పడుట. కావున ‘ బొమ్మపడు ఘటన, బొరుసు పడు ‘ఘటనకు పూరక ఘటన అవుతుంది.
(ii) పాచికతో 1 పడుట అనేది 2, 3, 4, 5, 6 పడుట అనే ఘటనలకు పూరక ఘటనయేనా? (పేజీ.నెం.311)
సాధన.
అవును, పూరక ఘటనలే.
‘1’ అను సంఖ్యను పొందు సంభావ్యత = \(\frac{1}{6}\) [P(E)]
2,3,4,5,6 సంఖ్యలను పొందు సంభావ్యత = P(\(\overline{\mathrm{E}}\)) = \(\frac{5}{6}\)
∴ P(E) + P(\(\overline{\mathrm{E}}\)) = \(\frac{1}{6}\) [P(E)] + \(\frac{5}{6}\)
= \(\frac{1}{6}\) [P(E)] = 1.
![]()
(iii) పరస్పరం పూరక ఘటనలయ్యే జతలకు 5 ఉదాహరణలు ఇవ్వండి. (పేజీ నెం. 311).
సాధన.
ఎ) ఒక పాచికను . దొర్లించినపుడు సరిసంఖ్య పడే ఘటన, బేసిసంఖ్య పడే ఘటనలు ఒకదానికొకటి పరస్పరం పూరక ఘటనలు అగును.
బి) ఒక పేకకట్ట నుండి ఎరుపు పేకముక్క లేదా నలుపు పేక ముక్క పొందే ఘటనలు పరస్పరం పూరక ఘటనలు అగును.
సి) 1,2,… 8 సంఖ్యల నుండి సరి లేదా బేసి సంఖ్యలను యాదృచ్ఛికంగా ఎన్నుకొను ఘటనలు పరస్పరం పూరక ఘటనలు అగును.
డి) వారం రోజులలో ఒక ఆదివారం లేదా మిగిలిన 6 రోజులలో ఆదివారం కాకుండుట అనే ఘటనలు పరస్పరం పూరక ఘటనలు.
ఇ) పరుగు పందెంలో గెలుపు మరియు ఓటముల సంభావ్యతలు పరస్పరం పూరక ఘటనలు.
![]()
ప్రయత్నించండి:
ప్రశ్న 1.
ఒక పాప వద్ద గల పాచిక ముఖంపై A,B,C,D,E,F లని ముద్రించబడి యున్నది. ఆ పాచికను దొర్లించినపుడు
(i) A
(ii) D పడే సంభావ్యతలను లెక్కించండి. (పేజీ నెం. 312)
సాధన.
మొత్తం పర్యవసానాల సంఖ్య = {A, B, C, D, E, F} = 6
(i) ‘A’ పడే అనుకూల పర్యవసానాల సంఖ్య = 1
‘A’ ను పొందు సంభావ్యత = P(A)
= ‘A’ కు గల అనుకూల పర్యవసానాల సంఖ్య / సాధ్యపడు మొత్తం పర్యవసానాల సంఖ్య
= \(\frac{1}{6}\)
(ii) ‘D’ పడే అనుకూల పర్యవసానాల సంఖ్య = 1
‘D’ ను పొందు సంభావ్యత = P(D)
= ‘D’ కు గల అనుకూల పర్యవసానాల సంఖ్య / సాధ్యపడు మొత్తం పర్యవసానాల సంఖ్య
= \(\frac{1}{6}\)
ప్రశ్న 2.
క్రింది వానిలో ఏవి ఒక ఘటన యొక్క సంభావ్యతను సూచించలేవు? (పేజీ నెం. 312)
(a) 2.3
(b) – 1.5
(c) 15 %
(d) 0.7
సాధన.
a) 2.3 ఒక ఘటన యొక్క సంభావ్యతను సూచించలేదు.
b) – 1.5 ఒక ఘటన యొక్క సంభావ్యతను సూచించలేదు.
c) 15 % ఒక ఘటన యొక్క సంభావ్యతను సూచిస్తుంది.
d) 0.7 ఒక ఘటన యొక్క సంభావ్యతను సూచిస్తుంది.
![]()
ప్రశ్న 3.
మీ దగ్గర ఒక కట్ట పేకాట కార్డులు బాగుగా కలుపబడి ఉన్నాయి అనుకొనండి. వాటి నుండి యాదృచ్చికముగా తీసిన కార్డు
1. రాణి అగుటకు సంభావ్యత ఎంత?
2. ముఖ కార్డు అగుటకు సంభావ్యత ఎంత?
3. స్పేడ్ అగుటకు సంభావ్యత ఎంత?
4. స్పేడ్, ముఖకార్డు అగుటకు సంభావ్యత ఎంత?
5. ముఖకార్డు కాకపోవుటకు సంభావ్యత ఎంత? (పేజీ నెం. 313, 314)
సాధన.
1. మొత్తం సాధ్యపడు పర్యవసానాల సంఖ్య = 52
రాణి పేక ముక్కను పొందు అనుకూల పర్యవసానాల సంఖ్య = 4 ![]()
రాణి ముక్కను పొందు సంభావ్యత = P(E)
= అనుకూల పర్యవసానాల సంఖ్య / సాధ్యపడు మొత్తం పర్యవసానాల సంఖ్య
= \(\frac{4}{52}-\frac{1}{13}\)
2. ముఖ కార్లు గల ముక్కలు J, Q, K.
ముఖ కార్డు పొందు అనుకూల పర్యవసానాలు = 4 × 3 = 12
సాధ్యపడు అన్ని పర్యవసానాల సంఖ్య = 52
∴ P(E) = అనుకూల పర్యవసానాల సంఖ్య/ సాధ్యపడు మొత్తం పర్యవసానాల సంఖ్య
= \(\frac{12}{52}-\frac{3}{13}\)
3. స్పేడ్ ముక్కల సంఖ్య = 13
మొత్తం కార్డుల సంఖ్య = 52
∴ కావలసిన సంభావ్యత = స్పేడ్ కార్డులగుటకు గల అనుకూల పర్యవసానాల సంఖ్య / సాధ్యపడు అన్ని పర్యవసానాల సంఖ్య
= \(\frac{13}{52}-\frac{3}{13}\)
![]()
4. స్పేడ్, ముఖకార్డు అగుటకు గల ‘అనుకూల పర్యవసానాల సంఖ్య = ![]() = 3
= 3
అన్ని పర్యవసానాల సంఖ్య = 52
∴ సంభావ్యత P(E) = \(\frac{3}{52}\)
5. స్పేడ్ ముఖ కార్డు అగుటకు సంభావ్యత P(E) = \(\frac{12}{52}\)
∴ స్పేడ్ ముఖ కార్డు కాకుండుటకు సంభావ్యత = P(\(\overline{\mathrm{E}}\)) = 1 – P(E)
= 1 – \(\frac{12}{52}\)
= \(\frac{52-12}{52}\)
= \(\frac{40}{52}\) = \(\frac{10}{13}\)
(లేదా)
స్పేడ్ ముఖ కార్డు కాకుండుటకు అనుకూల పర్య వసానాల సంఖ్య = 40 (52-12 = 40]
మొత్తం పర్యవసానాల సంఖ్య = 52
∴ సంభావ్యత = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం సాధ్యపడు పర్యవసానాల సంఖ్య _ 40 _ 10
= \(\frac{40}{52}\) = \(\frac{10}{13}\).
![]()
ఆలోచించి, చర్చించి, రాయండి:
ప్రశ్న 1.
ఏదైనా ఆటలో ఏ జట్టువారు మొదటి బంతిని తీసుకోవాలో నిర్ణయించడానికి నాణెమును వేయడమే నిష్పాక్షికం అంటారెందుకు? (పేజీ నెం. 312)
సాధన.
బొమ్మ పడుటకు గల సంభావ్యత = \(\frac{1}{2}\)
బొరుసు పడుటకు గల సంభావ్యత = \(\frac{1}{2}\)
రెండు ఘటనల సంభావ్యత సమానం. కనుక
∴ నాణెం ఎగురవేయుటయే నిష్పాక్షికం.
ప్రశ్న 2.
ఒక ఘటన యొక్క సంభావ్యత \(\frac{7}{2}\) ఉంటుందా? వివరించండి. (పేజీ నెం. 312)
సాధన.
ఒక ఘటన యొక్క సంభావ్యత \(\frac{7}{2}\) అగుట అసాధ్యం .
\(\frac{7}{2}\) = 3 \(\frac{1}{2}\), ఇది 1 కన్నా ఎక్కువ
∴ ఏ ఘటన యొక్క సంభావ్యతైనా ‘0’ నుండి ‘1’ వరకు ఉండును. [0 ≤ P(E) ≤ 1]. కావున అసాధ్యము.
![]()
ప్రశ్న 3.
క్రింది వాటిలో ఏయే వాదనలు సత్యములు?
(i) రెండు నాణెములు ఎగురవేసినప్పుడు 3 పర్యవసానాలు ఉంటాయి. రెండు బొమ్మలు, రెండు బొరుసులు, ఒక్కటి బొమ్మ మరొకటి బొరుసు. కనుక ఒక్కొక్క పర్యవసానము యొక్క సంభావ్యత \(\frac{1}{3}\).
(ii) ఒక పాచికను దొర్లించినపుడు పడేది సరిసంఖ్య లేక బేసి సంఖ్య. కావున బేసి సంఖ్య పడే సంభావ్యత (పేజీ నెం. 312)
సాధన.
(i) ఇది అసత్యము.
కారణం : అన్ని పర్యవసానాల సంఖ్య = 4. అవి, HH, HT, TH, TT.
∴ రెండు బొమ్మలు పడు సంభావ్యత = \(\frac{1}{4}\)
రెండు బొరుసులు పడు సంభావ్యత = \(\frac{1}{4}\)
ఒక బొమ్మ లేదా బొరుసు పడుటకు సంభావ్యత = \(\frac{2}{4}=\frac{1}{4}\)
(ii) సత్యం .
కారణం : సాధ్యపడే మొత్తం పర్యవసానాల సంఖ్య = 6 = {1, 2, 3, 4, 5, 6}
బేసిసంఖ్య పొందుటకు అనుకూల పర్యవసానాల సంఖ్య = 3 = {1, 3, 5}
సరిసంఖ్య పొందుటకు అనుకూల పర్యవసానాల సంఖ్య = (2, 4, 6) = 3
∴ బేసిసంఖ్య పడే సంభావ్యత P(E) = \(\frac{3}{6}=\frac{1}{2}\).
![]()
ఉదాహరణలు:
ప్రశ్న 1.
ఒక నాణెమును ఒకసారి ఎగురవేసినప్పుడు బొమ్మపడే సంభావ్యతను, బొరుసు పడే సంభావ్యతను లెక్కించండి. (పేజీ నెం. 309)
సాధన.
నాణెమును ఒకసారి ఎగురవేసినప్పుడు సాధ్యపడు పర్యవసానములు రెండు, బొమ్మ (H) లేక బొరుసు (T). బొమ్మ పడుట అనే ఘటన E అయితే అనుకూల పర్యవసానములు 1.
P(E) = P (బొమ్మ) = Eకు అనుకూల పర్యవసానాల సంఖ్య / సాధ్యపడు మొత్తం పర్యవసానాల సంఖ్య
= \(\frac{1}{2}\)
ఇదే విధంగా బొరుసు పడు అనే ఘటన F అయిన
P(F) = P (బొరుసు) = \(\frac{1}{2}\)
ప్రశ్న 2.
ఒక సంచిలో ఒక ఎరుపు బంతి, ఒక నీలం బంతి, ఒక పసుపు రంగు బంతి ఉన్నాయి. అన్ని బంతులు ఒకే పరిమాణము కలిగి ఉన్నాయి. సంచిలోనికి చూడకుండా మానస ఒక బంతిని తీస్తే ఆ బంతి
(i) పసుపు రంగు బంతి
(ii) ఎరుపు బంతి
(iii) నీలం బంతి అవడానికి ‘ సంభావ్యతలు కనుగొనండి. (పేజీ నెం. 309)
సాధన.
మానస చూడకుండా బంతిని తీసుకున్నది.
కావున అన్ని పర్యవసానములు సమసంభవములు. పసుపు రంగు బంతిని తీయు ఘటన Y, నీలం బంతి తీయు ఘటన B మరియు ఎరుపు బంతి తీయు ఘటన R అయిన ప్రతిరూప ఆవరణము {Y, B, R}.
పర్యవసానములు = 3.
(i) Y కి అనుకూల పర్యవసానములు = 1.
∴ P(Y) = \(\frac{1}{3}\)
అదే విధముగా P(R) = \(\frac{1}{3}\), P(B) = \(\frac{1}{3}\).
![]()
ప్రశ్న 3.
ఒక పాచికను ఒకసారి దొర్లించినపుడు
(i) 4 కన్నా ఎక్కువ పడు ఘటన సంభావ్యత
(ii) 4 లేక అంతకన్నా తక్కువ పడు ఘటన సంభావ్యతను కనుగొనండి. (పేజీ నెం. 310)
9985174864
సాధన.
(i) ఒక పాచికను దొర్లించినపుడు ప్రతిరూప ఆవరణము S = {1, 2, 3, 4, 5, 6}
మొత్తం పర్యవసానములు n(S)= 6
4 కన్నా ఎక్కువ’ అను ఘటనకు అనుకూల పర్యవసానాలు E = {5, 6}
E కు అనుకూల పర్యవసానాల సంఖ్య n(E) = 2
∴ ఘటన E యొక్క సంభావ్యత P(E) = \(\frac{2}{6}=\frac{1}{3}\)
![]()
(ii) F అనే ఘటన 4 లేక అంతకన్నా తక్కువ పడుట అయిన ప్రతిరూప ఆవరణము S = {1, 2, 3, 4, 5, 6 }
మొత్తం పర్యవసానాలు n(S) = 6
F కు అనుకూల పర్యవసానాలు F = {1, 2, 3, 4}
అనుకూల పర్యవసానాల సంఖ్య n(F)= 4
∴ ఘటన F యొక్క సంభావ్యత P(F) = \(\frac{4}{6}=\frac{2}{3}\)
ప్రశ్న 4.
బాగుగా కలుపబడిన పేకాట కార్డుల కట్టలో 52 కార్డుల నుండి’ ఒక్క కార్డు తీయుటలో అది
(i) ఏస్ అగుటకు
(ii) ఏస్ కాకపోవుటకు సంభావ్యతలను లెక్కించండి. (పేజీ నెం. 313)
సాధన.
కార్డులు బాగుగా కలుపబడ్డాయి. కావున పర్యవసానాలన్నీ సమసంభవములుగా పరిగణించాలి.
(i) ఒక కట్టలో 4 ఏన్లు ఉంటాయి. తీసుకొన్న కార్డు ఏస్ అవడం అనే ఘటన E అయితే E కు అనుకూల పర్యవసానాల సంఖ్య = 4
మొత్తం పర్యవసానాల సంఖ్య = 52
∴ కార్డు ఏస్ అగుటకు సంభావ్యత, .
P(E) = \(\frac{4}{52}=\frac{1}{13}\)
(ii) తీసుకున్న కార్డు ఏస్ కాదు అనే ఘటన F అయితే F కు అనుకూల పర్యవసానాల సంఖ్య = 52 – 4 = 48
మొత్తం పర్యవసానాల సంఖ్య = 52
∴ కార్డు ఏస్ కాకపోవుటకు సంభావ్యత P(F) = \(\frac{48}{52}=\frac{12}{13}\)
ప్రత్యామ్నాయ పద్ధతి :
ఘటన F అనగా E కానిది \(\overline{\mathrm{E}}\) కావున పూరక ఘటనలను ఉపయోగించి F యొక్క సంభావ్యత కనుగొనవచ్చు.
P(F) = P(\(\overline{\mathrm{E}}\)) = 1 – P(E)
= 1 – \(\frac{1}{13}\) = \(\frac{12}{3}\).
![]()
ప్రశ్న 5.
సంగీత, రేష్మాలు టెన్నిస్ ఆటను ఆడుతున్నారు. సంగీత గెలిచే సంభావ్యత 0.62 అయినప్పుడు రేష్మ గెలిచే సంభాష్యత కనుగొనండి. (పేజీ నెం. 314)
సాధన.
సంగీత, రేష్మాలు ఆటను గెలిచే ఘటనలను S, Rలు సూచిస్తున్నాయి అనుకొనుము.
సంగీత గెలిచే సంభావ్యత = P(S) = 0.62 (దత్తాంశం)
పూరక సంభావ్యతలను అనుసరించి, రేష్మ గెలిచే సంభావ్యత = P(R) = 1 – P(S)
= 1 – 0.62 = 0.38
ప్రశ్న 6.
శారద, హమీద మంచి స్నేహితులు. వారిద్దరి పుట్టిన రోజు పండుగలు సంవత్సరంలో (లీపు సంవత్సరం . కాదు)
(i) వేరువేరు రోజు రావడానికి?
(ii) ఒకే రోజు రావడానికి సంభాష్యతలు లెక్కించండి. (పేజీ నెం. 314)
సాధన.
సంవత్సరంలో 365 రోజులలో ఇద్దరిలో ఎవరి పుట్టిన రోజు అయినా ఏరోజు అయినా రావచ్చును. కావున మొత్తం 365 పర్యవసానాలు సమసంభవములని పరిగణించాలి.
(i) శారద, హమీదల పుట్టినరోజులు వేరువేరు రోజులు అవడానికి అనుకూల పర్యవసానాలు
= 365 – 1 = 364
∴ P (వేరువేరు పుట్టినరోజులు) = \(\frac{364}{365}\)
(ii) P (ఒకే రోజు పుట్టినరోజు) = 1 – P (వేరు వేరు పుట్టినరోజులు)
= 1 – \(\frac{364}{365}\) = \(\frac{1}{365}\)
![]()
ప్రశ్న 7.
40 మంది విద్యార్థులు గల తరగతిలో 25 మంది బాలికలు, 16 మంది బాలురు’ ఉన్నారు. తరగతి ప్రతినిధిని నియమించడానికై, వారి ఉపాధ్యాయురాలు అందరి పేర్లను విడివిడి కార్డులపై వ్రాసి, ఒక పెట్టెలో వేసి బాగా కలిపి, ఒక కార్డును తీశారు. ఆ కార్డుపై పేరు i) అమ్మాయి లేక ii) అబ్బాయిది కావడానికి సంభావ్యతలు లెక్కించండి. =(పేజీ నెం. 315)
సాధన.
కార్డులన్నీ. సమానం అయితే 40 మందిలో ఎవరి పేరు కార్డు అయినా రావచ్చును.
మొత్తం పర్యవసానాల సంఖ్య = 40
(i) తీసిన కార్డుపై అమ్మాయి పేరు ఉండడానికి అనుకూల పర్యవసానాల సంఖ్య = 25
∴ P(అమ్మాయి పేరుగల కార్డు) = P(అమ్మాయి)
= \(\frac{25}{40}=\frac{5}{8}\)
(ii) తీసిన కార్డుపై అబ్బాయి పేరు ఉండడానికి అనుకూల పర్యవసానాలు = 15
∴ P (అబ్బాయి పేరు గల కార్డు) = P (అబ్బాయి)
= \(\frac{15}{40}=\frac{3}{8}\)
(లేదా)
P (అబ్బాయి) = 1 – P (అబ్బాయి. కానిది)
= 1 – P (అమ్మాయి)
= 1 – \(\frac{5}{8}\) = \(\frac{3}{8}\)
![]()
ప్రశ్న 8.
ఒక పెట్టెలో 3 నీలం, 2 తెలుపు, 4 ఎరుపు గోళీలు కలవు. యాదృచ్ఛికంగా పెట్టె నుండి ఒక గోళీను తీసుకొంటే అది (i) తెలుపు
(ii) నీలం
(iii)ఎరుపు రంగు గోళీ అగుటకు సంభావ్యతలు గమనించండి. (పేజీ నెం. 316)
సాధన.
యాదృచ్ఛికంగా గోళీను తీసుకొనుట అనగా అన్ని పర్యవసానాలు సమసంభవాలు.
∴ ప్రతిరూప ఆవరణలోని పర్యవసానాల సంఖ్య = 3 + 2 + 4 = 9.
తెల్లని గోళీ తీయు ఘటనను W చే, నీలం గోళీ తీయు ఘటనను B చే, ఎరుపు గోళీ తీయు ఘటనను R చే గుర్తిస్తే
(i) W కు అనుకూల పర్యవసానాల సంఖ్య = 2
∴ P(W) = \(\frac{2}{9}\)
అదేవిధంగా,
(ii)P(B) = \(\frac{3}{9}=\frac{1}{3}\)
(iii) P(R) = \(\frac{4}{9}\)
∴ గమనిక P(W) + P(B) + P(R) = 1.
ప్రశ్న 9.
హర్ఫీత్ రెండు నాణెములను (₹ 1 మరియు ₹ 2) ఒకేసారి ఎగురవేసినాడు. కనీసం ఒక బొమ్మ పడుటకు సంభావ్యత కనుగొనండి. (పేజీ నెం. 317)
సాధన.
బొమ్మను Hతో, బొరుసును Tతో సూచిస్తే, రెండు నాణెములు ఎగురవేసినప్పుడు ఏర్పడు అన్ని , పర్యవసానములు (H, H), (H, T), (T, H), (T, T) ఇవి అన్నీ సమసంభవాలే. ఇందు (H, H) అనగా మొదటి నాణెం (₹ 1) బొమ్మ, రెండవ నాణెం (₹ 2) బొమ్మ అని అర్థం. అట్లే (H, T) అనగా మొదటి నాణెం బొమ్మ రెండవ నాణెం బొరుసు అని అర్థం. అట్లే మిగిలిన పర్యవసానాలు.
కనీసం ఒక బొమ్మకు అనుకూల పర్యవసానాలు E = {(H, H), (H, T), (T, H)}
E కు అనుకూల పర్యవసానాల సంఖ్య n(E) = 3.
∴ P(E) = \(\frac{3}{4}\)
(∵ ప్రతిరూప ఆవరణలో పర్యవసానాలు = 4)
అనగా హర్పీత్ కనీసం ఒక బొమ్మ పొందే సంభావ్యత = \(\frac{3}{4}\).
![]()
ప్రశ్న 10.
(వార్షిక పరీక్షలకు కాదు) మ్యూజికల్ చైర్స్ ఆటలో, ఆట మొదలైన 2 నిమిషాల లోపు ఏదో ఒక సమయంలో పాట ఆగుతుంది. ఆటగాళ్ళు ఆగాలి. అయితే ఆట మొదలైన \(\frac{1}{2}\) నిమిషంలోపు పాట ఆపు ఘటనకు సంభావ్యతను లెక్కించండి. (పేజీ నెం. 317)
సాధన.
పాట ఆపు సమయం యొక్క పర్యవసానాలు 0 మరియు 2ల మధ్య గల అన్ని వాస్తవ సంఖ్యలు. దీనిని సంఖ్యారేఖపై సూచిస్తే….

ఈ నిమిషంలోపు పాట ఆగును అను ఘటనకు E ను సూచిస్తే Eకు అనుకూల పర్యవసానములు అనగా సంఖ్యారేఖపై 0, \(\frac{1}{2}\), ల మధ్య గల అన్ని బిందువులు ) కు, 2కు మధ్యగల దూరం 2 అయిన 0, \(\frac{1}{2}\)ల మధ్య దూరం \(\frac{1}{2}\) అవుతుంది. ప్రయోగంలోని అన్ని పర్యవసానములన్నీ సమ సంభవములు కావున మొత్తం దూరం (కాలం) 2 అని, E కు అనుకూల దూరం (కాలం) అని పరిగణించవచ్చును.
∴ P(E) = E అనుకూల దూరము / మొత్తం దూరము
= \(\frac{\frac{1}{2}}{2}=\frac{1}{4}\)
ప్రశ్న 11.
క్రింది పటంలో చూపబడిన దీర్ఘచతురస్రాకార ప్రాంతంలో ఒక హెలికాప్టరు ‘ కూలిపోయిందని సమాచారం వచ్చింది. అది కొలను (lake)లో కూలిపోయి ఉండుటకు సంభావ్యత ఎంత? (పేజీ నెం. 318)
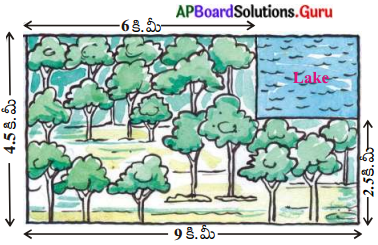
సాధన.
మొత్తం దీర్ఘచతురస్రాకార స్థలములో హెలికాప్టర్ ఏ, బిందువు వద్ద అయినా కూలి ఉండవచ్చును.
∴ ఘటన S జరుగుటకు పూర్తి స్థల వైశాల్యము
n(s) = (4.5 × 9) కి.మీ.2 = 40.5 కి.మీ.2
ఘటన E జరుగుటకు అనుకూల ప్రాంతము
n(E) = (2 × 3) కి.మీ.2 = 6 కి.మీ.2
∴ P (హెలికాప్టరు సరస్సులో కూలుట) = \(\frac{6}{40.5}=\frac{4}{27}\).
![]()
ప్రశ్న 12.
ఒక పెట్టెలోని 100 చొక్కాలలో 88 సరిగ్గా ఉన్నవి. 8 చొక్కాలు కొద్ది లోపాలను, 4 చొక్కాలు ఎక్కువ లోపాలను కలిగి ఉన్నాయి. జానీ అనే వ్యాపారి మంచి చొక్కాలను మాత్రమే కొంటాడు. సుజాత అను మరొక వ్యాపారి ఎక్కువ లోపాలున్న చొక్కాలను మాత్రమే నిరాకరిస్తుంది. (కొనదు). పెట్టెలో నుండి యాదృచ్ఛికంగా ఒక చొక్కాను తీస్తే ఎవరు కొనే సంభావ్యత ఎంత?
(i) జానీ
(ii) సుజాత. (పేజీ నెం. 318)
సాధన.
పెట్టెలోని 100 చొక్కాలలో నుండి 1 చొక్కా యాదృచ్ఛికంగా తీయబడినది అనగా పర్యవసానములన్నీ సమసంభవాలు.
(i) జానీ కొనుటకు అనుకూల పర్యవసానాలు = 88
P (జానీ చొక్కాను కొనుట) = \(\frac{88}{100}\) = 0.88
(ii)సుజాత చొక్కా కొనుటకు అనుకూల పర్యవసానాలు = 88 + 8 = 96
P(సుజాత చొక్కాను కొనుట) = \(\frac{96}{100}\) = 0.96.
ప్రశ్న 13.
రెండు పాచికలు, ఒకటి ఎర్రనిది, ఒకటి పసుపుది, ఒకేసారి దొర్లించడం జరిగింది. సాధ్యపడు అన్ని పర్యవసానములను పేర్కొనండి. రెండు పాచికలపై కనిపించే సంఖ్యల మొత్తం.
(i) 8
(ii) 13 మరియు
(iii) 12 లేక అంతకన్నా తక్కువ అవడానికి సంభావ్యతలు ఎంతెంత? (పేజీ నెం. 319)
సాధన.
ఎరుపు పాచికపై 1 ఉన్నప్పుడు తెలుపు పాచికపై 1, 2, 3, 4, 5 లేక. 6 ఏదయినా ఉండవచ్చును. అట్లే ఎరుపు పాచికపై ‘2’, ‘3’, ‘4’, ‘5’ లేక ‘6’ లు ఉన్నప్పుడు కూడా వివిధ పర్యవసానములు ఉంటాయి. ప్రయోగంలో సాధ్యపడు అన్ని పర్యవసానములు పట్టికలో క్రమయుగ్మాలుగా చూపబడ్డాయి. ప్రతి క్రమయుగ్మంలో మొదటిది ఎరుపు పాచికపై సంఖ్య, రెండవది తెలుపు పాచికపై సంఖ్య.
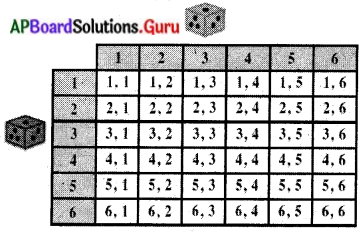
కావున ఉదాహరణకు (1,4), (4, 1) క్రమయుగ్మాలు సమానం కావు.
∴ మొత్తం సాధ్యపడు పర్యవసానాల సంఖ్య n(S) = 6 × 6 = 36.
(i) ఘటన E (రెండు సంఖ్యల మొత్తం 8) యొక్క అనుకూల పర్యవసానాలు = {{2, 6), (3, 5), (4, 4), (5, 3), (6, 2)}
E కు అనుకూల పర్యవసానాల సంఖ్య n(E) = 5
∴ P(E) = \(\frac{\mathrm{n}(\mathrm{E})}{\mathrm{n}(\mathrm{S})}=\frac{5}{36}\)
(ii) ఘటన F (రెండు సంఖ్యల మొత్తం 13) కు అనుకూల పర్యవసానాలు శూన్యము.
∴ P(F) = \(\frac{0}{36}\) = 0.
(iii) ఘటన G (12 లేక అంతకన్నా తక్కువ)కు అన్ని పర్యవసానాలు అనుకూలములే.
∴ P(G) = \(\frac{36}{36}\) = 1.