AP Board 10th Class Maths Solutions Chapter 3 బహుపదులు Exercise 3.4

SCERT AP 10th Class Maths Textbook Solutions Chapter 3 బహుపదులు Exercise 3.4 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 3rd Lesson బహుపదులు Exercise 3.4

ప్రశ్న 1.
కింద ఇవ్వబడిన బహుపదులలో p(x) బహుపదిని g(x) బహుపదిచే భాగించి భాగఫలాన్ని, శేషాన్ని కనుగొనండి.
(i) p(x) = x³ – 3x² + 5x – 3, g(x) = x² – 2
(ii) p(x) = x⁴ – 3x² + 4x + 5, g(x) = x² + 1 – x
(iii) p(x) = x⁴ – 5x + 6, g(x) = 2 – x²
సాధన.
(i) p(x) = x³ – 3x² + 5x – 3, g(x) = x² – 2

భాగఫలంలో మొదటి పదం = \(\frac{x^{3}}{x^{2}}\) = x

భాగఫలంలో రెండవ పదం = \(\frac{-3 x^{2}}{x^{2}}\) = – 3
భాగఫలం q(x) = x – 3
శేషం r (x) = 7x – 9

2వ పద్ధతి :
p(x) = x³ – 3x² + 5x – 3,
g(x) = x² – 2 = x² + 0x – 2

భాగఫలంలో మొదటి పదం = \(\frac{x^{3}}{x^{2}}\) = x

భాగఫలంలో రెండవ పదం = \(\frac{-3 x^{2}}{x^{2}}\) = – 3
భాగఫలం q(x) = x – 3
శేషము r(x) = 7x – 9

(ii) p(x) = x⁴ – 3x² + 4x + 5,
g(x) = x² + 1 – x
సాధారణ రూపంలో p(x) = x⁴ + 0x³ – 3x² + 4x + 5
అవరోహణ క్రమంలో g(x) = x² – x + 1

భాగఫలంలో మొదటి పదం = \(\frac{x^{4}}{x^{2}}\) = x

భాగఫలంలో రెండవ పదం =\(\frac{x^{3}}{x^{2}}\) = x

భాగఫలంలో మొదటి పదం = \(\frac{-3 x^{2}}{x^{2}}\) = – 3

భాగఫలం q(x) = x² + x – 3
శేషం r (x) = 8.

(iii) p(x) = x⁴ – 5x + 6, g(x) = 2 – x²
సాధారణ రూపంలో
p(x) = x⁴ + 0x³ + 0x² – 5x + 6
సాధారణ రూపంలో g(x) = – x² + 0x + 2

భాగఫలంలో మొదటి పదం = \(\frac{x^{4}}{-x^{2}}\) = – x²

భాగఫలంలో రెండవ పదం = \(\frac{2 x^{2}}{-x^{2}}\) = – 2

భాగఫలం q(x) = – x² – 2;
శేషం r (x) = – 5x + 10.

ప్రశ్న 2.
కింది బహుపదులలో రెండవ బహుపదిని, మొదటి బహుపదిచే భాగించి ప్రతి సందర్భంలో మొదటి బహుపది కారణాంకం అగునో, కాదో సరిచూడండి.
(i) t³ – 3, 2t⁴ + 3t³ – 2t² – 9t – 12
(ii) x² + 3x + 1, 3x⁴ + 5x³ – 7x² + 2x + 2
(iii) x³ – 3x + 1, x⁵ – 4x³ + x² + 3x + 1
సాధన.
(i) t² – 3, 2t⁴ + 3t³ – 2t² – 9t- 12

భాగఫలంలో మొదటి పదం = \(\frac{2 t^{4}}{t^{2}}\) = 2t²

భాగఫలంలో రెండవ పదం = \(\frac{3 \mathrm{t}^{3}}{\mathrm{t}^{2}}\) = 3t

భాగఫలంలో మూడవ పదం = \(\frac{4 \mathrm{t}^{2}}{\mathrm{t}^{2}}\) = 4

శేషం r (x) = 0
∴ t² – 3, 2t⁴ + 3t³ – 2t² – 9t – 12 కు కారణాంకము అవుతుంది.

(ii) x² + 3x + 1, 3x⁴ + 5x³ – 7x² + 2x + 2

భాగఫలంలో మొదటి పదం = \(\frac{3 x^{4}}{x^{2}}\) = 3 x²

భాగఫలంలో రెండవ పదం = \(\frac{-4 x^{3}}{x^{2}}\) = – 4 x

బాగఫలంలో మూడవ పదం = \(\frac{2 x^{2}}{x^{2}}\) = 2
శేషం r (x) = 0
∴ x² + 3x + 1, 3x⁴ + 5x³ – 7x² + 2x + 2 కారణాంకము అవుతుంది.

(iii) x³ – 3x + 1, x⁵ – 4x³ + x² + 3x + 1

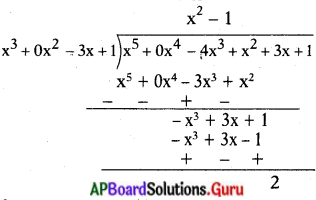
భాగఫలంలో మొదటి పదం = \(\frac{x^{5}}{x^{3}}\) = x²

భాగఫలంలో రెండవ పదం = \(\frac{-x^{3}}{x^{3}}\) = – 1
శేషం r (x) = 2
∴ x³ – 3x + 1, x⁵ – 4x³ + x² + 3x + 1 కు కారణాంకము కాదు.

ప్రశ్న 3.
3x⁴ + 6x³ – 2x² – 10x – 5 అను బహుపదికి రెండు శూన్యాలను \(\sqrt{\frac{5}{3}}\) మరియు – \(\sqrt{\frac{5}{3}}\) అయిన మిగిలిన రెండు శూన్యాలను కనుగొనండి.
సాధన.
p(x) = 3x⁴ + 6x³ – 2x² – 10x – 5
అయిన మిగిలిన రెండు
p(x) = \(\sqrt{\frac{5}{3}}\) మరియు – \(\sqrt{\frac{5}{3}}\) లు రెండు శూన్య విలువలు కావున (x – \(\sqrt{\frac{5}{3}}\)) (x + \(\sqrt{\frac{5}{3}}\))
= x² – \(\frac{5}{3}\) p(x) కు ఒక కారణాంకం అవుతుంది.

భాగఫలంలో మొదటి పదం = \(\frac{3 x^{4}}{x^{2}}\) = 3x²

భాగఫలంలో రెండవ పదం = \(\frac{6 x^{3}}{x^{2}}\) = 6x

భాగఫలంలో మూడవ పదం = \(\frac{3 x^{2}}{x^{2}}\) = 3

భాగహార అల్ గారిథమ్ ప్రకారం
3x⁴ + 6x³ – 2x² – 10x – 5
= (x² – \(\frac{5}{3}\)) (3x² + 6x + 3) + 0
= (x² – \(\frac{5}{3}\)) (3x² + 6x + 3)
p(x) = 0 అయిన
(x² – \(\frac{5}{3}\)) (3x² + 6x + 3) = 0
x² – \(\frac{5}{3}\) = 0 లేదా 3x² + 6x + 3 = 0
x² = \(\frac{5}{3}\) లేదా 3(x² + 2x + 1) = 0
x = ± \(\sqrt{\frac{5}{3}}\) లేదా 3(x + 1)² = 0
(x + 1)² = 0
x + 1 = 0
∴ x = – 1
p(x) యొక్క శూన్య విలువలు \(\sqrt{\frac{5}{3}}\), – \(\sqrt{\frac{5}{3}}\) మరియు – 1.

2వ పద్గతి:
p(x) = 3x⁴ + 6x³ – 2x² – 10x – 5 \(\sqrt{\frac{5}{3}}\) మరియు – \(\sqrt{\frac{5}{3}}\) లు p(x) యొక్క రెండు శూన్య విలువలు.
(x – \(\sqrt{\frac{5}{3}}\)) (x + \(\sqrt{\frac{5}{3}}\)) = x² – \(\frac{5}{3}\)
= \(\frac{3 x^{2}-5}{3}\)
= \(\frac{1}{3}\) (3x² – 5), p(x) కు కారణాంకం అవుతుంది. కాబట్టి p(x) కు 3x – 5 కారణాంకము

భాగఫలంలో మొదటి పదం = \(\frac{3 x^{4}}{3 x^{2}}\) = x²

భాగఫలంలో రెండవ పదం = \(\frac{6 x^{3}}{3 x^{2}}\) = 2x

భాగఫలంలో మూడవ పదం = \(\frac{3 x^{2}}{3 x^{2}}\) = 1

భాగహార అల్గారిథమ్ ప్రకారం p(x) = 3x⁴ + 6x³ – 2x² – 10x – 5
= (3x² – 5) (x² + 2x + 1) + 0
∴ p(x) = (3x² – 5) (x² + 2x + 1)
p(x) = 0 అయిన (3x² – 5) (x² + 2x + 1) = 0
3x² – 5 = 0 లేదా x² + 2x + 1 = 0
3x² = 5 లేదా (x + 1)² = 0
x² = , లేదా x + 1 = 0
x = ±\(\sqrt{\frac{5}{3}}\) లేదా x = – 1
∴ p(x) యొక్క శూన్య విలువలు \(\sqrt{\frac{5}{3}}\), – \(\sqrt{\frac{5}{3}}\) మరియు – 1.

ప్రశ్న 4.
x³ – 3x² + x + 2 అను బహుపదిని g(x) అనే బహుపదిచే భాగిస్తే భాగఫలము x – 2 మరియు శేషము – 2x + 4 అయిన g(x) ను కనుగొనండి.
సాధన.
p(x) = x³ – 3x² + x + 2
g(x) = ?
q(x) = x – 2
r(x) = – 2x + 4
భాగహార అల్ గారిథమ్ నుండి
p(x) = g(x) . q(x) + r(x)
p(x) – r(x) = g(x) . q(x)
x³ – 3x² + x + 2 – (- 2x + 4) = g(x) (x – 2)
x³ – 3x² + x + 2 + 2x – 4 = g(x) (x – 2)
x³ – 3x² + 3x – 2 = g(x) (x – 2)

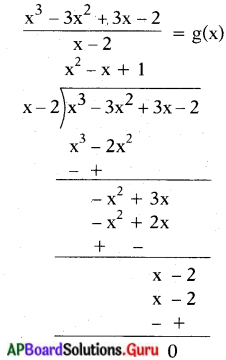
భాగఫలంలో మొదటి పదం = \(\frac{x^{3}}{x}\) = x²

భాగఫలంలో రెండవ పదం = \(\frac{-x^{2}}{x}\) = – x

భాగఫలంలో మూడవ పదం = \(\frac{x}{x}\) = 1
∴ g(x) = x = x + 1.

ప్రశ్న 5.
భాగహార నియమము మరియు దిగువ ఇవ్వబడిన నియమాలను తృప్తిపరిచే విధంగా p(x), g(x), q{x) మరియు r(x) బహుపదులకు తగిన ఉదాహరణలను ఇవ్వండి.
(i) p(x) పరిమాణము = q(x) పరిమాణము
(ii) q(x) పరిమాణము = r(x) పరిమాణము
(iii) r(x) పరిమాణము = 0
సాధన.
(i) p(x) పరిమాణం = q(x) పరిమాణం భాగహార అల్గారిథమ్
p(x) = g(x) q(x) + r(x)
ఉదా – 1: p(x) పరిమాణం = q(x) పరిమాణం కావాలంటే g(x) యొక్క పరిమాణం శూన్యం కావాలి అనగా g(x) స్థిర బహుపది.
3x³ – 15x² + 9x + 12
= 3(x³ – 5x² + 3x + 4) + 0
p(x) = 3x³ – 15x² + 9x + 12
g(x) = 3
q(x) = x³ – 5x² + 3x + 4
r(x) = 0

ఉదా – 2 : 15x² + 8x + 10
= 5 (3x² + \(\frac{8}{5}\) x + 2) + 0
p(x) = 15x² + 8x + 10
g(x) = 5
q(x) = 3x² + \(\frac{8}{5}\) x + 2
r(x) = 0

(ii) q(x) పరిమాణం = r(x) పరిమాణం భాగహార అల్ గారిథమ్ p(x) = g(x) q(x) + r(x) లెక్క ప్రకారం
q(x) పరిమాణం = r(x) పరిమాణం
r(x) పరిమాణం < g(x) పరిమాణము అని మనకు తెలుసు.
∴ q(x) పరిమాణం < g(x) పరిమాణం కావాలి

ఉదా -1 : p(x) = (x² + 5x + 6) (x + 3) + x – 4
= x³ + 5x² + 6x + 3x² + 15x + 18 + x – 4
p(x) = x³ + 8x + 22x + 14
g(x) = x² + 5x + 6
q(x) = x + 3
r(x) = x – 4

ఉదా – 2: p(x) = (3x³ – 4x + 5) (x² – 2) + x² + 2x + 5
= 3x⁵ – 4x³ + 5x² – 6x³ + 8x – 10 + x² + 2x + 5
p(x) = 3x⁵ – 10x³ + 6x² + 10x – 5
g(x) = 3x³ – 4x + 5
q(x) = x² – 2
r(x) = x² + 2x + 5

(iii) r(x) పరిమాణం = 0
r(x) పరిమాణం = 0 అనగా f(x) స్థిర బహుపది అవుతుంది.
ఉదా – 1: r(x) = 5
g(x) = x + 5
q(x) = x + 5x + 7
భాగహార అల్ గారిథమ్
p(x) = g(x) . q(x) + r(x) .
= (x + 5) (x² + 5x + 7) + 5
p(x) = x³ + 5x² + 7x + 5x² + 25x + 35 + 5
p(x) = x³ + 10x² + 32x + 40.

ఉదా – 2:
r(x) = 8
g(x) = x – 3
q(x) = x + 3
p(x) = g(x) . q(x) + r(x)
p(x) = (x – 3) (x + 3) +8
p(x) = x² – 9 + 8
p(x) = x² – 1