SCERT AP 10th Class Maths Textbook Solutions Chapter 7 నిరూపక రేఖాగణితం Exercise 7.1 Textbook Exercise Questions and Answers.
AP State Syllabus 10th Class Maths Solutions 7th Lesson నిరూపక రేఖాగణితం Exercise 7.1
ప్రశ్న 1.
కింద ఇవ్వబడిన బిందువుల మధ్య దూరంను కనుగొనండి.
(i) (2, 3) మరియు (4, 1)
సాధన.
A (2, 3) మరియు B (4, 1)
రెండు బిందువుల మధ్య దూరం
d = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
A, B ల మధ్య దూరం
d = \(\sqrt{(4-2)^{2}+(1-3)^{2}}\)
= \(\sqrt{2^{2}+(-2)^{2}}=\sqrt{4+4}=\sqrt{8}\)
∴ AB = 2√2 యూనిట్లు.
(ii) (- 5, 7) మరియు (- 1, 3)
సాధన.
A (- 5, 7) మరియు B (- 1, 3)
AB = d = \(\sqrt{\left(\mathrm{x}_{2}-\mathrm{x}_{1}\right)^{2}+\left(\mathrm{y}_{2}-\mathrm{y}_{1}\right)^{2}}\)
= \(\sqrt{(-1+5)^{2}+(3-7)^{2}}\)
= \(\sqrt{(-1+5)^{2}+(-4)^{2}}\)
= \(\sqrt{16+16}=\sqrt{32}=4 \sqrt{2}\)
∴ AB = 4√2 యూనిట్లు.
![]()
(iii) (- 2, – 3) మరియు (3, 2)
సాధన.
A (- 2, – 3) మరియు B (3, 2)
AB = d = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{[3-(-2)]^{2}+[2-(-3)]^{2}}\)
= \(\sqrt{(3+2)^{2}+(2+3)^{2}}\)
= \(\sqrt{25+25}=\sqrt{50}=5 \sqrt{2}\)
∴ AB = 5√2 యూనిట్లు.
(iv) (a, b) మరియు (-a, -b) . సాధన. A (a, b) మరియు B (-a, – b)
AB = d = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{(-a-a)^{2}+(-b-b)^{2}}\)
= \(\sqrt{(-2 a)^{2}+(-2 b)^{2}}=\sqrt{4\left(a^{2}+b^{2}\right)}\)
= \(2 \sqrt{a^{2}+b^{2}}\)
∴ AB = 2\(2 \sqrt{a^{2}+b^{2}}\) యూనిట్లు.
ప్రశ్న 2.
బిందువులు (0, 0) మరియు (36, 15) ల : మధ్య దూరాన్ని కనుగొనండి.
సాధన.
మూల బిందువు: (0, 0) నుండి (x, y ) బిందువు దూరం = \(\sqrt{x^{2}+y^{2}}\)
(0, 0), (36, 15) బిందువుల మధ్య దూరం = \(\sqrt{36^{2}+15^{2}}=\sqrt{1296+225}\)
= \(\sqrt{1521}\) = 39
(0, 0), (36, 15) బిందువుల మధ్య దూరం = 39 యూనిట్లు.
![]()
ప్రశ్న 3.
బిందువులు (1, 5), (2, 3) మరియు (- 2, – 1) లు సరేఖీయాలో, కాదో సరిచూడండి.
సాధన.
ఇచ్చిన బిందువులు
A (1, 5), B (2, 3), C (- 2, – 1) అనుకుందాం.
AB = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{(2-1)^{2}+(3-5)^{2}}\)
= \(\sqrt{1^{2}+(-2)^{2}}=\sqrt{1+4}=\sqrt{5}\)
BC = \(\sqrt{(-2-2)^{2}+(-1-3)^{2}}\)
= \(\sqrt{(-4)^{2}+(-4)^{2}}\)
= \(\sqrt{16+16}=\sqrt{32}=4 \sqrt{2}\)
AC = \(\sqrt{(-2-1)^{2}+(-1-5)^{2}}\)
= \(\sqrt{(-3)^{2}+(-6)^{2}}\)
= \(\sqrt{9+36}=\sqrt{45}=3 \sqrt{5}\)
ఏ రెండు కొలతలైనా (రేఖాఖండాల పొడవులు) మూడవ కొలతకు సమానం కాదు. కావున పై మూడు బిందువులు సరేఖీయాలు కావు.
![]()
ప్రశ్న 4.
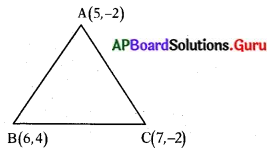
బిందువులు (5, -2), (6,4) మరియు (7, -2)లు ఒక సమద్విబాహు త్రిభుజం యొక్క శీర్షాలు అవుతాయో? కావో ? చూడండి.
సాధన.
ఇచ్చిన బిందువులు A = (5, – 2), B = (6, 4), C = (7, – 2) లు ∆ABC శీర్షాలు అనుకొందాం.
AB = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{(6-5)^{2}+(4-(-2))^{2}}\)
= \(\sqrt{1+36}=\sqrt{37}\)
BC = \(\sqrt{(7-6)^{2}+(-2-4)^{2}}\)
= \(\sqrt{1+36}=\sqrt{37}\)
∴ ∆ABC లో AB = BC
కావున ఇచ్చిన బిందువులు ఒక సమద్విబాహు త్రిభుజ శీర్షాలు అవుతాయి.
ప్రశ్న 5.
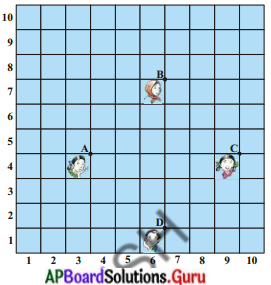
పటంలో చూపినట్లు, ఒక తరగతిలో నలుగురు స్నేహితురాళ్ళు A, B, C, D స్థానాల్లో తరగతిలో అటూ ఇటూ తిరుగుతూ కొన్ని నిమిషాలు పరిశీలించిన తర్వాత, జరీనా ఫణిని ఇలా అడిగింది. “ABCD ఒక చతురస్రం అవుతుందని నీవు భావించడం లేదా ?” అందుకు ఫణి ఒప్పుకోలేదు. ” బిందువుల మధ్య దూరంనకు సూత్రాన్నుపయోగించి – ఎవరి సమాధానం సరైనది ? ఎందుకు ? తెలపండి.
సాధన.
పై పటం నుండి A, B, C, D నిరూపకాలు A (3, 4), B (6, 7), C (9, 4), D (6, 1)
లు
AB = \(\sqrt{\left(\mathrm{x}_{2}-\mathrm{x}_{1}\right)^{2}+\left(\mathrm{y}_{2}-\mathrm{y}_{1}\right)^{2}}\)
= \(\sqrt{(6-3)^{2}+(7-4)^{2}}=\sqrt{3^{2}+3^{2}}\)
= \(\sqrt{9+9}=\sqrt{18}=3 \sqrt{2}\)
BC = \(\sqrt{(9-6)^{2}+(4-7)^{2}}\)
= \(\sqrt{3^{2}+(-3)^{2}}=\sqrt{9+9}=\sqrt{18}=3 \sqrt{2}\)
CD = \(\sqrt{(6-9)^{2}+(1-4)^{2}}\)
= \(\sqrt{(-3)^{2}+(-3)^{2}}\)
= \(\sqrt{9+9}=\sqrt{18}=3 \sqrt{2}\)
DA = \(\sqrt{(6-3)^{2}+(1-4)^{2}}\)
= \(\sqrt{3^{2}+(-3)^{2}}\)
= \(\sqrt{9+9}=\sqrt{18}=3 \sqrt{2}\)
AB = BC = CD = DA
కర్ణాలు AC = \(\sqrt{(9-3)^{2}+(4-4)^{2}}\)
= \(\sqrt{6^{2}+0}=\sqrt{36}\) = 6 యూనిట్లు.
BD = \(\sqrt{(6-6)^{2}+(1-7)^{2}}\)
= \(\sqrt{0+(-6)^{2}}=\sqrt{36}\) = 6 యూనిట్లు.
AC = BD
□ ABCD యొక్క నాలుగు భుజాలు సమానం మరియు కర్ణాలు కూడా సమానాలు. కావున ABCD ఒక చతురస్రం అవుతుంది. కాబట్టి జరీనా సమాధానము సరైనది.
(లేదా)
AB2 + BC2 = 18 + 18 = 36 = AC2
పైథాగరస్ సిద్దాంత విషర్యము నుండి ∠B = 90° అవుతుంది. AB = BC = CD = DA మరియు ∠B = 90°.
కావున □ ABCD ఒక చతురస్రము.
![]()
ప్రశ్న 6.
బిందువులు A(a, 0), B(- a, 0), C(0, a√3) అనునవి ఒక సమబాహు త్రిభుజాన్ని ఏర్పరచగలవని చూపండి.
సాధన.
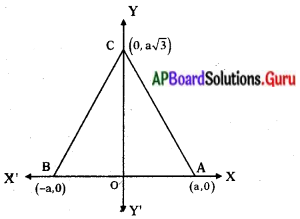
త్రిభుజ శీర్షాలు A (a, 0), B (- a, 0), C (o, a√3).
AB = | – a – a| = |- 2a| = 2a యూనిట్లు
BC = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{[0-(-a)]^{2}+(a \sqrt{3}-0)^{2}}\)
= \(\sqrt{a^{2}+3 a^{2}}=\sqrt{4 a^{2}}\) = 2a యూనిట్లు.
AC = \(\sqrt{(0-a)^{2}+(a \sqrt{3}-0)^{2}}\)
= \(\sqrt{a^{2}+3 a^{2}}=\sqrt{4 a^{2}}\) = 2a యూనిట్లు.
∴ AB = BC = CA = 2a
∴ ∆ABC ఒక సమబాహు త్రిభుజం.
(∵ సమబాహు త్రిభుజంలో అన్ని భుజాలు సమానాలు).
![]()
ప్రశ్న 7.
బిందువులు (- 7, – 3), (5, 10), (15, 8) మరియు (3, – 5) లు వరుసగా ఒక సమాంతర చతుర్భుజానికి శీర్షాలు అవుతాయని చూపండి.
సాధన.
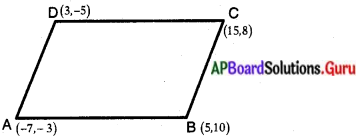
ఇచ్చిన బిందువులు A (- 1, – 3), B (5, 10), C (15, 8), D (3, – 5)
రెండు బిందువుల మధ్య దూరం = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
AB = \(\sqrt{[5-(-7)]^{2}+[10-(-3)]^{2}}\)
= \(\sqrt{12^{2}+13^{2}}=\sqrt{144+169}\)
= √313 యూనిట్లు
BC = \(\sqrt{(15-5)^{2}+(8-10)^{2}}\)
= \(\sqrt{(10)^{2}+(-2)^{2}}=\sqrt{100+4}\)
= \(\sqrt{100+4}=\sqrt{104}\) యూనిట్లు.
CD = \(\sqrt{(3-15)^{2}+[8-(-5)]^{2}}\)
= \(\sqrt{(-12)^{2}+13^{2}}=\sqrt{144+169}\)
= √313 యూనిట్లు
DA = \(\sqrt{(-7-3)^{2}+[-3-(-5)]^{2}}\)
= \(\sqrt{(-10)^{2}+2^{2}}\)
= \(\sqrt{100+4}=\sqrt{104}\) యూనిట్లు
పై కొలతల నుండి □ABCD చతుర్భుజంలో AB = CD మరియు BC = DA.
∴ □ABCD ఒక సమాంతర చతుర్భుజం అవుతుంది.
![]()
ప్రశ్న 8.
బిందువులు (- 4, – 7), (- 1, 2), (8, 5) మరియు (5, 4) లు వరుసగా ఒక సమచతుర్భుజం (రాంబస్) యొక్క శీర్షాలు అవుతాయని చూపండి. దాని వైశాల్యం కనుగొనండి. (సూచన : రాంబస్ వైశాల్యం = \(\frac{1}{2}\) × కర్ణముల లబ్ధం)
సాధన.
ఇచ్చిన బిందువులు AC(- 4, – 7), B (- 1, 2), C (8, 5), D (5, – 4)
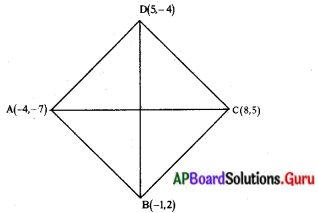
రెండు బిందువుల మధ్య దూరం = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
AB = \(\sqrt{[-1-(-4)]^{2}+[2-(-7)]^{2}}\)
= \(\sqrt{(3)^{2}+9^{2}}=\sqrt{9+81}\)
= √90 యూనిట్లు,
BC = \(\sqrt{[8-(-1)]^{2}+(5-2)^{2}}\)
= \(\sqrt{9^{2}+3^{2}}=\sqrt{81+9}\)
= √90 యూనిట్లు,
CD = \(\sqrt{(5-8)^{2}+(-4-5)^{2}}\)
= \(\sqrt{(-3)^{2}+(-9)^{2}}\)
= \(\sqrt{9+81}=\sqrt{90}\) యూనిట్లు.
DA = \(\sqrt{[5-(-4)]^{2}+[-7-(-4)]^{2}}\)
= \(\sqrt{9^{2}+(-3)^{2}}\)
= \(\sqrt{9+81}=\sqrt{90}\) యూనిట్లు.
పై కొలతల నుండి AB = BC = CD = DA.
కావున ఇచ్చిన నాలుగు బిందువులు వరుసగా ఒక సమచతుర్భుజం (రాంబస్)ను ఏర్పరుస్తాయి.
d1 = BD = \(\sqrt{5-(-1)^{2}+(-4-2)^{2}}\)
= \(\sqrt{6^{2}+(-6)^{2}}=\sqrt{36 \times 2}\)
= 6√2
d2 = AC = \(\sqrt{[8-(-4)]^{2}+[5-(-7)]^{2}}\)
= \(\sqrt{12^{2}+12^{2}}=\sqrt{144+144}\)
= \(\sqrt{2 \times 144}\) = 12√2
రాంబస్ వైశాల్యము = \(\frac{1}{2}\) × కర్ణాల లబ్ధం
= \(\frac{1}{2}\) d1d2
= \(\frac{1}{2}\) × 6√2 × 12√2
= 36 × 2 = 72 చ.యూ.
![]()
ప్రశ్న 9.
క్రింద ఇవ్వబడిన బిందువులతో ఏర్పడే చతుర్భుజం ఏ రకమైనది ? దాని పేరును తెలపండి. మీ సమాధానానికి సరైన కారణం తెలపండి.
(i) (- 1, – 2), (1, 0), (- 1, 2), (- 3, 0)
సాధన.
ఇచ్చిన బిందువులు A (- 1, – 2), B (1, 0), C (- 1, 2), D (- 3, 0)
రెండు బిందువుల మధ్య దూరం , d = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
AB = \(\sqrt{[1-(-1)]^{2}+[0-(-2)]^{2}}\)
= \(\sqrt{2^{2}+2^{2}}=\sqrt{4+4}=\sqrt{8}=2 \sqrt{2}\)
BC = \(\sqrt{(-1-1)^{2}+(2-0)^{2}}\)
= \(\sqrt{2^{2}+2^{2}}=\sqrt{4+4}=\sqrt{8}=2 \sqrt{2}\)
CD = \(\sqrt{[-3-(-1)]^{2}+(0-2)^{2}}\)
= \(\sqrt{2^{2}+2^{2}}=\sqrt{4+4}=\sqrt{8}=2 \sqrt{2}\)
DA = \(\sqrt{[-1-(-3)]^{2}+[0-(-2)]^{2}}\)
= \(\sqrt{2^{2}+2^{2}}=\sqrt{4+4}=\sqrt{8}=2 \sqrt{2}\)
∴ AB = BC = CD = DA.
ఇప్పుడు AC = \(\sqrt{[-1-(-1)]^{2}+[2-(-2)]^{2}}\)
= \(\sqrt{0^{2}+4^{2}}=\sqrt{16}\) = 4 యూనిట్లు
BD = \(\sqrt{(-3-1)^{2}+(0-0)^{2}}\)
= \(\sqrt{(-4)^{2}}=\sqrt{16}\) = 4 యూనిట్లు
∴ AC = BD.
ABCD బిందువులు ఏర్పరిచే చతుర్భుజంలో నాలుగు భుజాలు సమానం మరియు కర్ణాలు కూడా సమానము.
కావున ABCD ఒక చతురస్రం అవుతుంది.
![]()
(ii) (- 3, 5), (1, 10), (3, 1), (- 1, – 4)
సాధన.
ఇచ్చిన బిందువులు
A(- 3, 5), B(1, 10), C(3, 1), D(- 1, – 4)
\(\overline{\mathrm{AB}}=\sqrt{(1+3)^{2}+(10-5)^{2}}\)
= \(\sqrt{16+25}=\sqrt{41}\)
\(\overline{\mathrm{BC}}=\sqrt{(3-1)^{2}+(1-10)^{2}}\)
= \(\sqrt{4+81}=\sqrt{85}\)
\(\overline{C D}=\sqrt{(-1-3)^{2}+(-4-1)^{2}}\)
= \(\sqrt{16+25}=\sqrt{41}\)
\(\overline{\mathrm{AD}}=\sqrt{(-1+3)^{2}+(-4-5)^{2}}\)
= \(\sqrt{4+81}=\sqrt{85}\)
\(\overline{\mathrm{AC}}=\sqrt{(3+3)^{2}+(1-5)^{2}}\)
= \(\sqrt{36+16}=\sqrt{52}\)
\(\overline{\mathrm{BD}}=\sqrt{(-1-1)^{2}+(-4-10)^{2}}\)
= \(\sqrt{4+196}=\sqrt{200}=10 \sqrt{2}\)
□ABCD లో \(\overline{\mathrm{AB}}\) = \(\overline{\mathrm{CD}}\) మరియు \(\overline{\mathrm{BC}}\) = \(\overline{\mathrm{AD}}\) (∵ ఎదురెదురు భుజాలు సమానం) మరియు \(\overline{\mathrm{AC}}\) ≠ \(\overline{\mathrm{BD}}\).
కావున, □ABCD ఒక సమాంతర చతుర్భుజం. ఇచ్చిన బిందువులతో సమాంతర చతుర్భుజం ఏర్పడుతుంది.
□ABCD లో AB = CD, BC = AD మరియు AC ≠ BD.
![]()
(iii) (4, 5), (7, 6), (4, 3), (1, 2)
సాధన.
ఇచ్చిన బిందువులు
A (4, 5), B (7, 6), C (4, 3), D (1, 2)
d = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
AB = \(\sqrt{(7-4)^{2}+(6-5)^{2}}\)
= \(\sqrt{3^{2}+1^{2}}\)
= \(\sqrt{9+1}=\sqrt{10}\) యూనిట్లు
BC = \(\sqrt{(4-7)^{2}+(3-6)^{2}}\)
= \(\sqrt{(-3)^{2}+(-3)^{2}}\)
= \(\sqrt{9+9}=\sqrt{18}\)
= 3√2 యూనిట్లు
CD = \(\sqrt{(1-4)^{2}+(2-3)^{2}}\)
= \(\sqrt{(-3)^{2}+(-1)^{2}}\)
= \(\sqrt{9+9}\)
= √10 యూనిట్లు
DA = \(\sqrt{(4-1)^{2}+(5-2)^{2}}\)
= \(\sqrt{9+9}=\sqrt{18}=3 \sqrt{2}\) = 3√2 యూనిట్లు
AB = CD మరియు BC = DA
ఇప్పుడు కర్ణాలు AC = \(\sqrt{(4-4)^{2}+(3-5)^{2}}\)
= \(\sqrt{0+(-2)^{2}}=\sqrt{4}\) = 2 యూనిట్లు
BD = \(\sqrt{(1-7)^{2}+(2-6)^{2}}\)
= \(\sqrt{(-6)^{2}+(-4)^{2}}\)
= \(\sqrt{36+16}=\sqrt{52}\) యూనిట్లు
AC ≠ BD
∴ ABCD బిందువులతో ఏర్పడే చతర్భుజం యొక్క ఎదురెదురు భుజాలు సమానం మరియు కర్ణాలు అసమానాలు. కావున □ ABCD దీర్ఘచతురస్రం కానటువంటి సమాంతర చతుర్భుజాన్ని ఏర్పరుస్తుంది.
![]()
ప్రశ్న 10.
x-అక్షంపై ఉంటూ బిందువులు (2, – 5) మరియు (- 2, 9) లకు సమాన దూరంలోనున్న బిందువును కనుగొనండి.
సాధన.
x-అక్షంపై గల బిందువు (x, 0) రూపంలో ఉంటుంది.
P (x, 0) బిందువు A (2, – 5) మరియు B (- 2, 9) లకు సమాన దూరంలో కలదు అనుకొనుము.
∴ AP = BP ⇒ AP2 = BP2
AP = \(\sqrt{(2-x)^{2}+(-5-0)^{2}}\)
= \(\sqrt{4-4 x+x^{2}+25}\)
= \(\sqrt{x^{2}-4 x+29}\)
AP2 = x2 – 4x + 29
BP = \(\sqrt{(-2-x)^{2}+(9-0)^{2}}\)
= \(\sqrt{4+4 x+x^{2}+81}\)
= \(\sqrt{x^{2}+4 x+85}\)
BP2 = x2 + 4x + 85
AP2 = BP2.
x2 – 4x + 29 = x2 + 4x + 85
x2 – 4x – x2 – 4x = 85 – 29
– 8x = 56
8x = – 56 ⇒ x = \(\frac{-56}{8}\) = – 7
∴ కావలసిన బిందువు P= (- 7, 0)
సరిచూచుకోవడం :
AP = \(\sqrt{[2-(-7)]^{2}+(-5-0)^{2}}\)
= \(\sqrt{9^{2}+(-5)^{2}}=\sqrt{81+25}\)
= √107 యూనిట్లు
BP = \(\sqrt{[-2-(-7)]^{2}+(9-0)^{2}}\)
= \(\sqrt{5^{2}+9^{2}}=\sqrt{25+81}\)
= √107 యూనిట్లు.
![]()
ప్రశ్న 11.
బిందువులు (x, 7) మరియు (1, 15) ల మధ్య దూరం 10 యూనిట్లు, అయిన x విలువ ఎంత ?
సాధన.
ఇచ్చిన బిందువులు A (x, 7), B (1, 15)
AB = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{(1-x)^{2}+(15-7)^{2}}\)
= \(\sqrt{1-2 x+x^{2}+64}\)
AB = \(\sqrt{x^{2}-2 x+65}\)
లెక్క ప్రకారం AB = 10 యూనిట్లు
= \(\sqrt{x^{2}-2 x+65}\) = 10
ఇరువైపులా వర్గం చేయగా,
∴ x2 – 2x + 65 = 100
x2 – 2x + 65 – 100 = 0
x2 – 2x – 35 = 0
x2 – 7x + 5x – 35 = 0
x (x -7) + 5 (x – 7) = 0
(x – 7) (x + 5) = 0
x – 7 = 0 లేదా x + 5 = 0
x = 7 లేదా x = – 5
∴ x = 7 లేదా – 5.
![]()
ప్రశ్న12.
బిందువులు P(2, – 3) మరియు Q(10, y) ల మధ్య దూరం 10 యూనిట్లు, అయిన y విలువ ఎంత?
సాధన.
ఇచ్చిన బిందువులు P (2, – 3) మరియు Q (10, y)
PQ = \(\sqrt{(10-2)^{2}+[y-(-3)]^{2}}\)
= \(\sqrt{8^{2}+(y+3)^{2}}\)
= \(\sqrt{64+y^{2}+6 y+9}\)
= \(\sqrt{y^{2}+6 y+73}\)
లెక్క ప్రకారం PQ = 10 యూనిట్లు
\(\sqrt{y^{2}+6 y+73}\) = 10
y2 + 6y + 73 = 100 (∵ ఇరువైపులా వర్గం చేయగా)
y2 + 6y – 27 = 0
y2 + 9y – 3y – 27 = 0
y (y + 9) – 3 (y + 9) = 0
(y + 9) (y – 3) = 0 .
y + 9 = 0 లేదా y – 3 = 0
y = – 9 లేదా y = 3
∴ y = – 9 లేదా 3.
![]()
ప్రశ్న 13.
బిందువు, (- 5, 6) గుండా పోవు వృత్తం యొక్క కేంద్రం (3, 2) అయిన దాని వ్యాసార్ధంను కనుగొనండి.
సాధన.
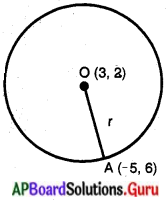
వృత్తకేంద్రం O = (3, 2)
వృత్తంపై ఒక బిందువు A = (- 5, 6)
వృత్త వ్యాసార్థం OA = \(\sqrt{(-5-3)^{2}+(6-2)^{2}}\)
= \(\sqrt{(-8)^{2}+4^{2}}=\sqrt{64+16}\) = √80
= \(\sqrt{16 \times 5}=\sqrt{4 \times 4 \times 5}\) = 4√5
వృత్త వ్యాసార్థం r = 4√5 యూనిట్లు.
![]()
ప్రశ్న 14.
బిందువులు (1, 5), (5, 8) మరియు (13, 14)లతో త్రిభుజమును గీయగలమా ? కారణం తెల్పండి.
సాధన.
ఇచ్చిన బిందువులు
A (1, 5), B (5, 8), C (13, 14)
∴ రెండు బిందువుల మధ్య దూరం
d = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
∴ AB = \(\sqrt{(5-1)^{2}+(8-5)^{2}}\)
= \(\sqrt{4^{2}+3^{2}}=\sqrt{16+9}\)
= √25 = 5
BC = \(\sqrt{(13-5)^{2}+(14-8)^{2}}\)
= \(\sqrt{8^{2}+6^{2}}=\sqrt{64+36}\)
= √100 = 10
AC = \(\sqrt{(13-1)^{2}+(14-5)^{2}}\)
= \(\sqrt{12^{2}+9^{2}}=\sqrt{144+81}\)
= √225 = 15
పై కొలతల నుండి, AB + BC = AC కావున A, B, C లు సరేఖీయాలు.
కాబట్టి A, B, C బిందువులగుండా త్రిభుజాన్ని గీయలేము.
![]()
ప్రశ్న 15.
బిందువు (x, y), (- 2, 8) మరియు (- 3, – 5) లకు సమాన దూరంలో ఉన్నది. అయిన x మరియు y ల
మధ్య సంబంధమును కనుక్కోండి.
సాధన.
ఇచ్చిన బిందువులు
P (x, y), A (- 2, 8), B (- 3, – 5) అనుకొనుము.
లెక్క ప్రకారం,
∴ AP = BP = AP2 = BP2 ……… (1)
∴ AP = \(\sqrt{[(-2-x)]^{2}+(8-y)^{2}}\)
= \(\sqrt{x^{2}+4 x+4+y^{2}-16 y+64}\)
AP2 = x2 + y2 + 4x – 16y + 68
BP = \(\sqrt{[x-(-3)]^{2}+[y-(-5)]^{2}}\)
= \(\sqrt{(x+3)^{2}+(y+5)^{2}}\)
= \(\sqrt{x^{2}+6 x+9+y^{2}+10 y+25}\)
BP = x2 + y2 + 6x + 10y + 34
AP = BP
∴ x2 + y2 + 4x – 16y + 68 = x2 + y2 + 6x + 10y + 34
x2 + y2 + 4x – 16y + 68 – x2 – y2 – 6x – 10y – 34 = 0
– 25 – 26y + 34 = 0
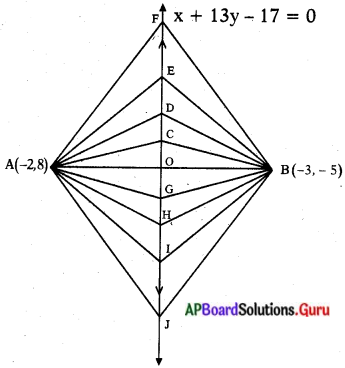
∴ – 2[x + 13y – 17] = 0
X + 13y = 17.
![]()
గమనిక : (- 3, – 5) మరియు (- 2, 8) లకు సమానదూరంలో గల బిందువులు C, D, E, F, G, H, I, J, ……. x + 13y – 17 = 0 సరళరేఖపై ఉంటాయి.
ఈ సరళరేఖ AB రేఖాఖండాన్ని లంబ సమద్విఖండన చేస్తుంది. ఒక రేఖండం యొక్క లంబ సమద్విఖండన రేఖపై గల బిందువులు ఆ రేఖాఖండం యొక్క చివరి బిందువులకు సమాన దూరంలో ఉంటాయి.