AP Board 10th Class Maths Solutions Chapter 8 సరూప త్రిభుజాలు Exercise 8.1

SCERT AP 10th Class Maths Textbook Solutions Chapter 8 సరూప త్రిభుజాలు Exercise 8.1 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 8th Lesson సరూప త్రిభుజాలు Exercise 8.1

ప్రశ్న 1.
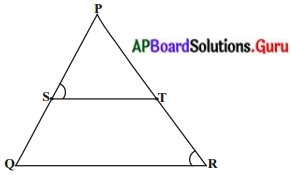
∆PQRS లో \(\frac{\mathbf{P S}}{\mathbf{S Q}}=\frac{\mathbf{P T}}{\mathbf{T R}}\) అగునట్లు ST ఒక సరళరేఖ, ఇంకనూ ∠PST = ∠PRQ అయిన ∆PQR ఒక సమద్విబాహు త్రిభుజమని చూపండి.

సాధన.
దత్తాంశము : ∆PQR లో \(\frac{\mathbf{P S}}{\mathbf{S Q}}=\frac{\mathbf{P T}}{\mathbf{T R}}\) మరియు
∠PST = ∠PRQ.
సారాంశము : ∆POR ఒక సమద్విబాహు త్రిభుజము.
ఉపపత్తి : \(\frac{\mathbf{P S}}{\mathbf{S Q}}=\frac{\mathbf{P T}}{\mathbf{T R}}\) కావున ST || QR
(థమిక సిద్ధాంతపు విపర్యయము నుండి)
∴ ∠PST = ∠POR ………… (1) (ST || QR కావున వాటి సదృశ్య కోణాలు)
మరియు, ∠PST = ∠PRQ……….. (2) (దత్తాంశము)
(1), (2) ల నుండి, ∠PQR = ∠PRQ
∴ PR = PQ [త్రిభుజంలో సమాన కోణాలకు ఎదురుగా ఉన్న భుజాలు సమానము)
కావున ∆PQR సమద్విబాహు త్రిభుజము.

ప్రశ్న 2.
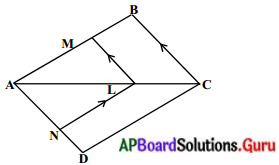
ఇచ్చిన పటంలో, LM || CB మరియు LN || CD అయిన AM = AN అని చూపండి.

సాధన.
దత్తాంశము : LM || CB మరియు LN || CD
∆ABC లో, LM || BC కావున

ప్రశ్న 3.
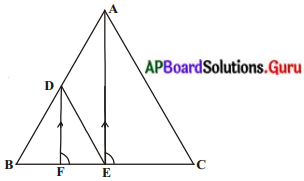
ఇచ్చిన పటంలో, DE || AC మరియు DF || AE అయిన BF = BE అని చూపండి.

సాధన.
∆ABC లో, DE || AC కావున
\(\frac{\mathrm{BE}}{\mathrm{EC}}=\frac{\mathrm{BD}}{\mathrm{DA}}\) …………. (1)
(థమిక సిద్ధాంతం నుండి) మరలా ∆ABE లో, DF || AE కావున
\(\frac{\mathrm{BF}}{\mathrm{FE}}=\frac{\mathrm{BD}}{\mathrm{DA}}\) …………. (2)
(1) మరియు (2) ల నుండి
\frac{B E}{E C}=\frac{B F}{F E}\(\) అని నిరూపించబడినది.

ప్రశ్న 4.
ఒక త్రిభుజములో ఒక భుజము మధ్య బిందువు గుండా పోయేరేఖ, రెండవ భుజానికి సమాంతరంగా ఉంటే అది మూడవ భుజాన్ని సమద్విఖండన చేస్తుందని చూపండి. (ప్రాథమిక అనుపాత సిద్ధాంతము నుపయోగించి)
సాధన.

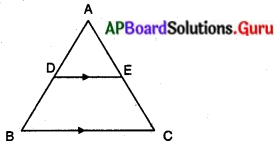
దత్తాంశము : AB మధ్య బిందువు D మరియు DE || BC
సారాంశము : AE = EC
నిరూపణ : ∆ABC లో DE || BC
∴ \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\) (ప్రాథమిక అనుపాత సిద్ధాంతము)

\(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\) [AB మధ్య బిందువు D ∴ AD = DB]
1 = \(\frac{\mathrm{AE}}{\mathrm{EC}}\)
∴ AE = EC
కావున DE, AC ని సమద్విఖండన చేస్తుంది.

ప్రశ్న5.
ఒక త్రిభుజములో రెండు భుజాల మధ్య బిందువులను కలిపే రేఖాఖండము మూడవ భుజానికి సమాంతరంగా ఉంటుందని చూపండి. (ప్రాథమిక అనుపాత సిద్ధాంత విపర్యయము నుపయోగించి)
సాధన.
దత్తాంశము : ∆ABC లో AB మధ్య బిందువు ‘D’
మరియు AC మధ్య బిందువు ‘E’.
సారాంశం : DE || BC.
ఉపపత్తి :

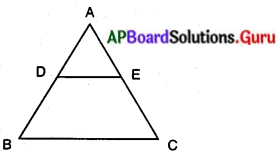
AB మధ్య బిందువు ‘D’,
AD = DB
⇒ \(\frac{\mathrm{AD}}{\mathrm{DB}}\) = 1 ………. (1)
మరియు AC మధ్య బిందువు ‘E’ అయిన
AE = EC
⇒ \(\frac{\mathrm{AE}}{\mathrm{EC}}\) = 1 ………… (2)
(1), (2) ల నుండి
\(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)
ఒక త్రిభుజంలో ఏవైనా రెండు భుజాలను ఒకే నిష్పత్తిలో విభజించు సరళరేఖ, మూడవ భుజానికి సమాంతరంగా నుండును.
∴ DE || BC [∴ ప్రాథమిక అనుపాత సిద్ధాంత విపర్యం నుండి నిరూపించబడినది].

ప్రశ్న 6.
ఇచ్చిన పటములో, DE || OQ మరియు DF || OR అయిన EF || QR అని చూపండి.

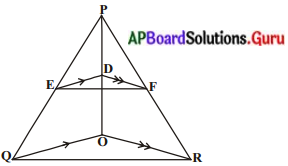
సాధన.
దత్తాంశము : ∆PQRలో DE || OQ; DF || OR
సారాంశము : EF || QR
ఉపపత్తి : ∆POQ లో DE || OQ, కావున ప్రాథమిక అనుపాత సిద్ధాంతమును అనుసరించి
\(\frac{\mathrm{PE}}{\mathrm{EQ}}=\frac{\mathrm{PD}}{\mathrm{DO}}\) ………………(1)
∆PQR లో DF || OR కావున ప్రాథమిక అనుపాత సిద్ధాంతమును అనుసరించి
\(\frac{\mathrm{PF}}{\mathrm{FR}}=\frac{\mathrm{PD}}{\mathrm{DO}}\) ……….. (2)
(1), (2) ల నుండి, \(\frac{\mathrm{PE}}{\mathrm{EQ}}=\frac{\mathrm{PF}}{\mathrm{FR}}\)
(1), (4) అంతు EQ , FR ఆ విధముగా APQR ను EF రేఖ PQ మరియు
PR లను ఒకే నిష్పత్తిలో విభజించుచున్నది.. కావున EF || QR. (ప్రాథమిక సిద్ధాంతపు విపర్యయం నుండి).

ప్రశ్న 7.
ఇచ్చిన పటంలో A, B, C లు వరుసగా OP, OQ మరియు OR లపై బిందువులు. AB || PQ మరియు AC || PR అయిన BC || QR అని చూపండి.

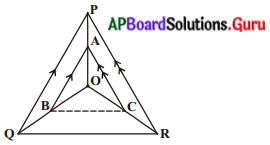
సాధన.
దత్తాంశము : ∆PQRలో AB || PQ; AC || PR.
సారాంశము : BC || QR
ఉపపత్తి : ∆POQలో AB || PQ కావున
\(\frac{\mathrm{OA}}{\mathrm{AP}}=\frac{\mathrm{OB}}{\mathrm{BQ}}\) ………… (1)
∆OPRలో AC || PR కావున
\(\frac{\mathrm{OA}}{\mathrm{AP}}=\frac{\mathrm{OC}}{\mathrm{CR}}\) ………… (2)
(1) మరియు (2) ల నుండి \(\frac{\mathrm{OB}}{\mathrm{BQ}}=\frac{\mathrm{OC}}{\mathrm{CR}}\)
ఆ విధముగా ∆OQR ను BC రేఖ OQ మరియు OR అను సమాన నిష్పత్తిలో విభజిస్తుంది.
∴ BC || QR.
[ప్రాథమిక సిద్ధాంత విపర్యయము నుండి)

ప్రశ్న 8.
ట్రెపీజియం ABCD లో AB||DC. దాని కర్ణములు పరస్పరం బిందువు ‘0’ వద్ద ఖండించుకొంటాయి. అయిన \(\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}\) అని చూపండి.
సాధన.
దత్తాంశము : ట్రెపీజియము ABCD లో AB || CD మరియు AC, BD కర్ణాలు ‘O’ వద్ద ఖండించుచున్నవి.
సారాంశము : \(\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}\)

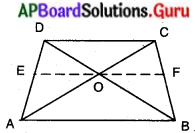
నిర్మాణము : EF అనురేఖను CD మరియు AB లకు సమాంతరంగా ఉంటూ ‘O’ గుండా పోవు విధంగా గీయుము.
ఉపపత్తి: ∆ACDలో EO // CD కావున AO _ AE
\(\frac{\mathrm{AO}}{\mathrm{CO}}=\frac{\mathrm{AE}}{\mathrm{DE}}\) …………… (1) [ప్రాథమిక అనుపాత సిద్ధాంతం నుండి]

∆ABD లో, EO || AB కావున
\(\frac{\mathrm{DE}}{\mathrm{AE}}=\frac{\mathrm{DO}}{\mathrm{BO}}\) [ప్రాథమిక అనుపాత సిద్ధాంతం నుండి)

\(\frac{\mathrm{BO}}{\mathrm{DO}}=\frac{\mathrm{AE}}{\mathrm{DE}}\) ……………… (2) [విలోమము చేయగా )
(1), (2) ల నుండి
\(\frac{\mathrm{AO}}{\mathrm{CO}}=\frac{\mathrm{BO}}{\mathrm{DO}}\)

⇒ \(\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}\) నిరూపించబడినది.

ప్రశ్న 9.
7.2 సెం.మీ పొడవు గల ఒక రేఖాఖండమును గీసి దానిని 5 : 3 నిష్పత్తిలో విభజించండి. ఏర్పడిన రెండు భాగముల పొడవులను కొలిచి రాయండి.
సాధన.

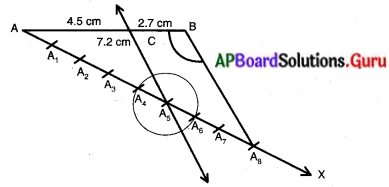
నిర్మాణ సోపానాలు :
(1) \(\overline{\mathrm{AB}}\) = 7.2 సెం. మీతో ఒక రేఖాఖండంను గీయుము.
2) ‘A’ వద్ద ∠BAX అను అల్పకోణంను గీయుము.
3) \(\stackrel{\leftrightarrow}{\mathrm{AX}}\) పై సమాన వ్యాసార్ధ కొలతలతో 5 + 3 = 8కి సమాన చాపములు (A₁, A₂, A₃, …… A₈) లను గీయుము.
4) A₈ మరియు B ను కలుపుము.
5) A₅ బిందువు గుండా \(\stackrel{\leftrightarrow}{A_{8} B}\) కి సమాంతర రేఖను గీయుము.
6) AB రేఖాఖండంను ‘C’ రేఖ 5 : 3 నిష్పత్తిలో ఖండించుచున్నది.
7) AC మరియు BC లను కొలవగా AC = 4.5 సెం.మీ. మరియు BC = 2.7 సెం.మీ.