AP SCERT 6th Class Maths Textbook Solutions Chapter 10 ప్రాయోజిక జ్యామితి Ex 10.4 Textbook Exercise Questions and Answers.
AP State Syllabus 6th Class Maths Solutions 10th Lesson దత్తాంశ నిర్వహణ Exercise 10.4
ప్రశ్న 1.
కోణమానిని ఉపయోగించకుండా \(\angle \mathrm{ABC}\) = 60° నిర్మించండి.
సాధన.
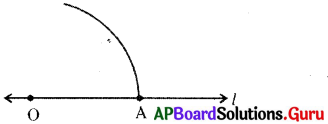
సోపానం – 1 : ‘l’ రేఖను గీచి దానిపై బిందువు ‘O’ ను గుర్తించాలి.
![]()
సోపానం – 2 : వృత్తలేఖిని లోహముల్లు ‘O’ మీద ఉంచి, కొంత వ్యాసార్ధంతో l ను A వద్ద ఖండించినట్లు ఒక చాపం గీయాలి.
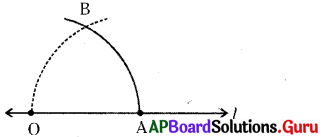
సోపానం – 3 : A కేంద్రంగా సోపానం 2 లోని వ్యాసార్ధంతో పై చాపాన్ని B వద్ద ఖండించేలా మరో చాపం గీయాలి.
సోపానం – 4 : OB లు కలపాలి. 60° కొలత గల \(\angle \mathrm{BOA}\) ఏర్పడింది.
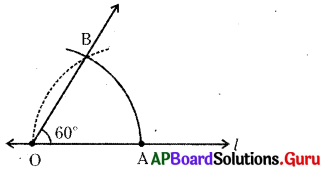
![]()
ప్రశ్న 2.
కోణమానిని మరియు వృత్తలేఖినిల సాయంతో 120° కోణం నిర్మించండి.
సాధన.
సోపానం – 1: OA కిరణం గీయాలి.
![]()
సోపానం – 2 : 0 కేంద్రంగా కొంత వ్యాసార్ధంతో OA ను M వద్ద ఖండించేలా ఒక చాపం గీయాలి.
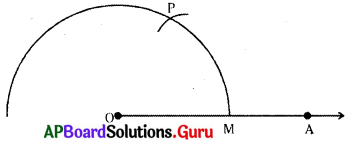
సోపానం – 3 : M కేంద్రంగా అదే వ్యాసార్ధంతో పై చాపాన్ని P వద్ద ఖండించేలా మరో చాపం గీయాలి.
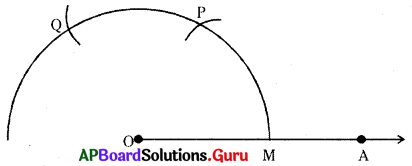
సోపానం – 4 : P కేంద్రంగా మరలా అదే వ్యాసార్ధంతో మొదటి చాపాన్ని Q వద్ద ఖండించేలా మరో చాపం గీయాలి.
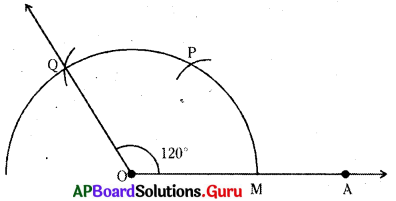
సోపానం – 5 : OQ లు కలపాలి. \(\angle \mathrm{AOQ}\) కావలసిన కోణం.
3. వృత్తలేఖిని, స్కేలు సాయంతో క్రింది కోణాలు నిర్మించి, నిర్మాణక్రమం రాయండి.
ప్రశ్న (అ)
75°
సాధన.
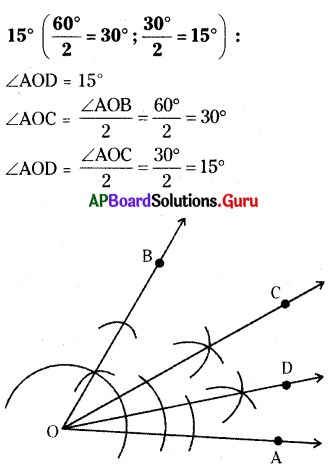
75° (60 + 15) :
\(\angle \mathrm{AOX}\) = 75°
\(\angle \mathrm{AOC}\) + \(\angle \mathrm{COX}\) = 60° + 15° = 75° .
నిర్మాణక్రమం :
- \(\angle \mathrm{AOC}\) = 60° మరియు \(\angle \mathrm{AOB}\) = 120° కోణాలను పై 2వ సమస్యలో వలె నిర్మించాలి.
- \(\angle \mathrm{COB}\) యొక్క కోణ సమద్విఖండన కిరణం \(\overrightarrow{\mathrm{OD}}\) ని నిర్మించాలి.
- ఇప్పుడు \(\angle \mathrm{AOD}\) = 90° (\(\angle \mathrm{AOC}\) + \(\angle \mathrm{COD}\) = 60° + 30° = 90°)
- \(\angle \mathrm{COD}\) = 30° యొక్క కోణ సమద్విఖండన కిరణం \(\overrightarrow{\mathrm{OX}}\) ని నిర్మించాలి.
- మనకు కావలసిన కోణం \(\angle \mathrm{AOX}\) = \(\angle \mathrm{AOC}\) + \(\angle \mathrm{COX}\) = 60° + 15° = 75° ఏర్పడినది.
![]()
ప్రశ్న (ఆ)
15°
సాధన.
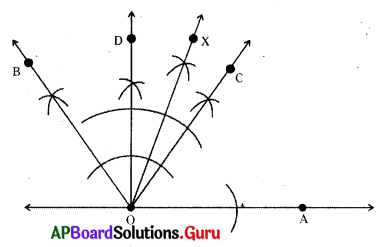
నిర్మాణక్రమం :
- \(\angle \mathrm{AOB}\) = 60° కోణాన్ని నిర్మించాలి.
- \(\angle \mathrm{AOB}\) యొక్క కోణ సమద్విఖండన కిరణం
- \(\overrightarrow{\mathrm{OC}}\) ని నిర్మించాలి.
- \(\angle \mathrm{AOC}\) = \(\angle \mathrm{COB}\) = 30° అవుతుంది.
- \(\angle \mathrm{AOC}\) యొక్క కోణ’ సమద్విఖండన కిరణం
- \(\overrightarrow{\mathrm{OD}}\) ని నిర్మించాలి.
- ఇప్పుడు మనకు కావలసిన కోణం \(\angle \mathrm{AOD}\) = \(\frac {30°}{2}\) = 15° ఏర్పడినది.
![]()
ప్రశ్న (ఇ)
105°
సాధన.
105° (90° + 15° = 105°) :
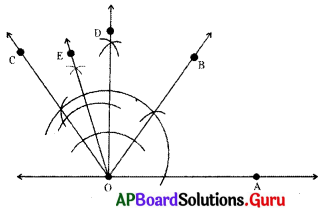
\(\angle \mathrm{AOE}\) = 105°
\(\angle \mathrm{AOB}\) + \(\angle \mathrm{BOD}\) + \(\angle \mathrm{DOE}\) = 60°+ 30° + 15° = 105°
నిర్మాణ క్రమం :
- \(\angle \mathrm{AOB}\) = 60° మరియు \(\angle \mathrm{AOC}\) = 120° ల కోణాలను నిర్మించాలి.
- \(\angle \mathrm{BOC}\) = 60° యొక్క కోణ సమద్విఖండన కిరణం
- \(\overrightarrow{\mathrm{OD}}\) ని నిర్మించాలి.
- ఇప్పుడు \(\angle \mathrm{AOD}\) = \(\angle \mathrm{AOB}\) + \(\angle \mathrm{BOD}\) = 60° + 30° = 90° అవుతుంది. అలాగే \(\angle \mathrm{DOC}\) = 30°
- \(\angle \mathrm{DOC}\) యొక్క కోణ సమద్విఖండన కిరణం \(\overrightarrow{\mathrm{OE}}\) ని నిర్మించాలి.
- ఇప్పుడు \(\angle \mathrm{DOE}\) = \(\frac {30°}{2}\) = 15° అవుతుంది.
- కావలసిన కోణం \(\angle \mathrm{AOE}\) = \(\angle \mathrm{AOD}\) + \(\angle \mathrm{DOE}\) = 90° + 15° = 105° ఏర్పడినది.