AP SCERT 6th Class Maths Textbook Solutions Chapter 10 ప్రాయోజిక జ్యామితి Ex 10.3 Textbook Exercise Questions and Answers.
AP State Syllabus 6th Class Maths Solutions 10th Lesson దత్తాంశ నిర్వహణ Exercise 10.3
1. కోణమానిని సాయంతో కింది కోణాలు నిర్మించండి.
ప్రశ్న (అ)
\(\angle \mathbf{A B C}\) = 65°
సాధన.
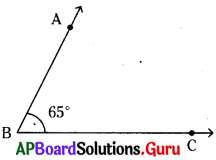
నిర్మాణము :
1. కొంత పొడవు గల \(\overrightarrow{\mathrm{BC}}\) కిరణం గీయవలెను.
2. కోణమానిని మధ్య బిందువును ‘B’ వద్ద ఉంచి \(\overrightarrow{\mathrm{BC}}\) ఆధారరేఖతో ఏకీభవించునట్లు చేయాలి.
3. 65° వద్ద ‘A’ బిందువును గుర్తించాలి.
4. BA లు కలపాలి. \(\angle \mathbf{A B C}\) = 65°.
![]()
ప్రశ్న (ఆ)
\(\angle \mathbf{P Q R}\) = 136°
సాధన.
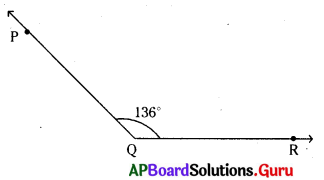
నిర్మాణము :
1. కొంత పొడవు గల \(\overrightarrow{\mathrm{QR}}\) కిరణం గీయవలెను.
2. కోణమానిని మధ్య బిందువును ‘Q’ వద్ద ఉంచి \(\overrightarrow{\mathrm{QR}}\) ఆధారరేఖతో ఏకీభవించునట్లు చేయాలి.
3. 136° వద్ద ‘P’ బిందువును గుర్తించాలి.
4. PQలు కలపాలి. \(\angle \mathbf{P Q R}\) = 136°.
ప్రశ్న (ఇ)
\(\angle \mathbf{Y}\) = 45°
సాధన.
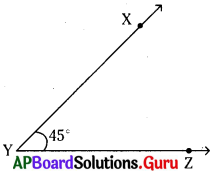
నిర్మాణము :
1. కొంత పొడవు గల \(\overline{\mathrm{YZ}}\) కిరణం గీయవలెను.
2. కోణమానిని మధ్య బిందువును ‘Y’ వద్ద ఉంచి \(\overline{\mathrm{YZ}}\) ఆధారరేఖతో ఏకీభవించునట్లు చేయాలి.
3. 45° వద్ద ‘X’ బిందువును గుర్తించాలి.
4. YXలు కలపాలి. \(\angle \mathrm{XYZ}\) = 45°.
![]()
ప్రశ్న (ఈ)
\(\angle \mathbf{O}\) = 172°
సాధన.

నిర్మాణము :
1. కొంత పొడవు గల \(\overline{\mathrm{OT}}\) కిరణం గీయవలెను.
2. కోణమానిని మధ్య బిందువును ‘O’ వద్ద ఉంచి \(\overline{\mathrm{OT}}\) ఆధారరేఖతో ఏకీభవించునట్లు చేయాలి.
3. 172° వద్ద ‘D’ బిందువును గుర్తించాలి.
4. OD లు కలపాలి. \(\angle \mathrm{DOT}\) = 172°.
ప్రశ్న 2.
కింది కోణాలను నీ నోట్ పుస్తకంలో కాపీ చేసి, వాటి కోణ సమద్విఖండన కిరణాలు గీయండి.
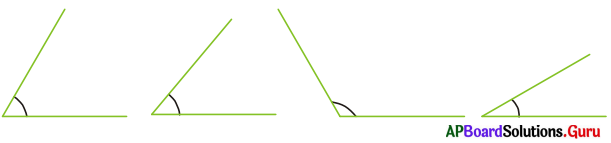
సాధన.
(i)
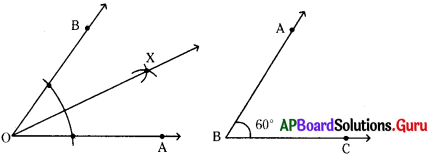
\(\angle \mathrm{AOB}\) యొక్క కోణ సమద్విఖండన కిరణం \(\overrightarrow{\mathrm{OX}}\).
\(\angle \mathrm{AOX}\) = \(\angle \mathrm{XOB}\)
(ii)
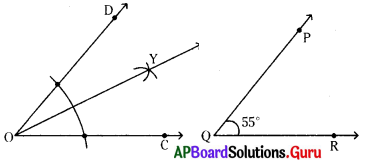
\(\angle \mathrm{COD}\) యొక్క కోణ సమద్విఖండన కిరణం \(\overrightarrow{\mathrm{OY}}\).
\(\angle \mathrm{COY}\) = \(\angle \mathrm{YOD}\)
![]()
(iii)
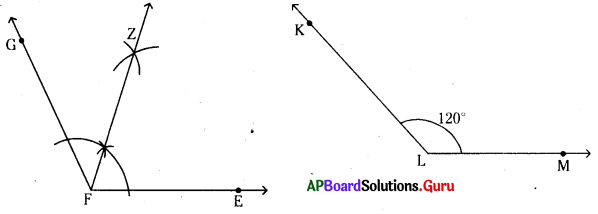
\(\angle \mathrm{EFG}\) యొక్క కోణ సమద్విఖండన కిరణం \(\overrightarrow{\mathrm{FZ}}\).
\(\angle \mathrm{EFZ}\) = \(\angle \mathrm{ZFG}\)
(iv)
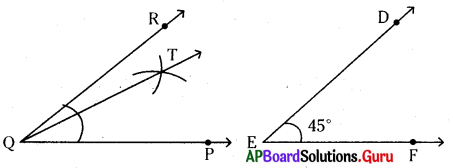
\(\angle \mathrm{PQR}\) యొక్క కోణ సమద్విఖండన కిరణం \(\overrightarrow{\mathrm{QT}}\)
\(\angle \mathrm{PQT}\) = \(\angle \mathrm{TQR}\)