SCERT AP 6th Class Maths Solutions Chapter 2 పూర్ణాంకాలు InText Questions and Answers.
AP State Syllabus 6th Class Maths Solutions 2nd Lesson పూర్ణాంకాలు InText Questions
[పేజి నెం. 17]
ఇప్పుడు ఇచ్చిన సంఖ్యలకు పూర్వ సంఖ్య, ఉత్తర సంఖ్యలతో కింది పట్టికను పూరించండి.
| క్ర.సం. | సహజసంఖ్య | దానిముందు సంఖ్య (పూర్వ సంఖ్య) | దాని తర్వాత సంఖ్య (ఉత్తర సంఖ్య) |
| 1. | 135 | ||
| 2. | 237 | ||
| 3. | 999 |
సాధన.
| క్ర.సం. | సహజసంఖ్య | దానిముందు సంఖ్య (పూర్వ సంఖ్య) | దాని తర్వాత సంఖ్య (ఉత్తర సంఖ్య) |
| 1. | 135 | 134 | 136 |
| 2. | 237 | 236 | 238 |
| 3. | 999 | 998 | 1000 |
చర్చించండి [పేజి నెం. 17]
ప్రశ్న 1.
ఏ సహజ సంఖ్యకు ఉత్తర సంఖ్య లేదు?
సాధన.
ప్రతి పూర్ణాంకానికి ఉత్తర సంఖ్య ఉంది.
ప్రశ్న 2.
ఏ సహజ సంఖ్యకు పూర్వ సంఖ్య లేదు ?
సాధన.
పూర్ణాంకాలన్నింటిలో ‘0’ (సున్నా)కి పూర్వ సంఖ్య లేదు.
![]()
నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 18]
కనిష్ఠ పూర్ణాంకమేది?
సాధన.
కనిష్ఠ పూర్ణాంకము ‘0’.
ఆలోచించండి [పేజి నెం. 18]
ప్రశ్న 1.
సహజ సంఖ్యలన్నీ పూర్ణాంకాలు అవుతాయా?
సాధన.
సహజ సంఖ్యలు అన్నీ పూర్ణాంకాలు అవుతాయి.
ప్రశ్న 2.
పూర్ణాంకాలన్నీ సహజసంఖ్యలు అవుతాయా?
సాధన.
పూర్ణాంకాలన్నీ సహజసంఖ్యలు కావు. ‘0’ పూర్ణాంకము.
కాని సహజ సంఖ్య కాదు. అనగా ‘0’ తప్ప మిగిలిన అన్ని పూర్ణాంకాలు సహజ సంఖ్యలు అవుతాయి.
ఇవి చేయండి [పేజి నెం. 19]
కింది వాటిని సంఖ్యారేఖపై సూచించండి.
అ) 5 + 3
సాదన.
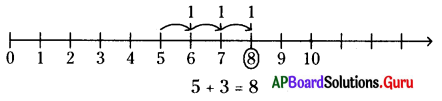
ఆ) 5 – 3
సాధన.
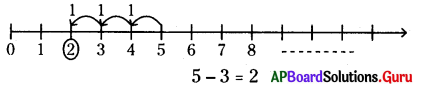
ఇ) 3 + 5
సాదన.
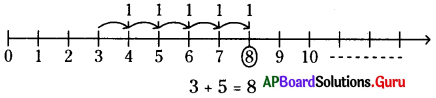
ఈ) 10 + 1
సాదన.
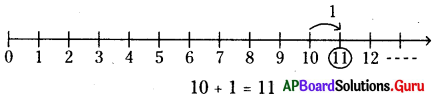
ఉ) 8 – 5
సాధన.

![]()
ప్రయత్నించండి [పేజి నెం. 19]
సంఖ్యారేఖను ఉపయోగించి కింది వాటిని కనుగొనండి.
ప్రశ్న 1.
5 రావాలంటే 8 నుండి ఏ సంఖ్యను తీసివేయాలి?
సాధన.

ప్రశ్న 2.
1 రావాలంటే 6 నుండి ఏ సంఖ్యను తీసివేయాలి?
సాధన.
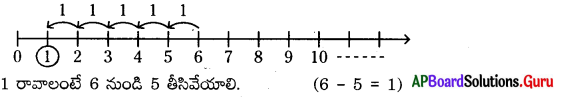
ప్రశ్న 3.
8 రావాలంటే 6 కి ఏ సంఖ్యను కలపాలి?
సాధన.

ప్రశ్న 4.
30 రావాలంటే ఎన్ని 6 లు అవసరం?
సాధన.

రాజు, గాయత్రిలు కలిసి సంఖ్యారేఖను తయారుచేసి దానిపై ఒక ఆట ఆడుతున్నారు.
సంఖ్యారేఖపై సున్న వద్ద ప్రారంభించి మొదటిసారి 3 ప్రమాణాలు, రెండవసారి 8 ప్రమాణాలు, మూడవసారి 5 ప్రమాణాల చొప్పున దూకితే నీవు చివరకు సంఖ్యారేఖపై ఎక్కడికి చేరుకుంటావు అని గాయత్రిని రాజు అడిగాడు. మొదటిసారి 3ని, రెండవసారి 11ని, చివరగా 16ని చేరుకుంటానని గాయత్రి సమాధానం చెప్పింది.
గాయత్రి సమాధానం సరియైనదని నీవు భావిస్తున్నావా ? గాయత్రి మార్గంను సంఖ్యారేఖపై సూచించండి.
సంకలన, వ్యవకలనాల ఆధారంగా ఈ ఆటను నీ మిత్రునితో కలిసి ఆడుము.
సాధన.
అవును. గాయత్రి సమాధానం సరియైనది.

![]()
ఆలోచించండి [పేజి నెం. 21]
ప్రశ్న 1.
పూర్ణాంకాల సమితి వ్యవకలనంలో సంవృత ధర్మాన్ని పాటిస్తుందా?
సాధన.
8, 5 లు పూర్ణాంకాలు. 8 – 5 = 3 ఒక పూర్ణాంకము.
5 – 8 = -3 పూర్ణాంకము కాదు.
కావున పూర్ణాంకాల సమితి వ్యవకలనంలో సంవృత ధర్మాన్ని పాటించదు.
ప్రశ్న 2.
పూర్ణాంకాల సమితి భాగహారంలో సంవృత ధర్మాన్ని పాటిస్తుందా?
సాధన.
6, 3 లు రెండు పూర్ణాంకాలు.
6 ÷ 3 = 2 ఒక పూర్ణాంకము
3 ÷ 6 = \(\frac {3}{6}\) పూర్ణాంకం కాదు.
కావున, పూర్ణాంకాల సమితి భాగహారంలో సంవృత ధర్మాన్ని పాటించదు.
నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 21]
ప్రశ్న 1.
12 ÷ 3 మరియు 42 ÷ 7 లను కనుగొనండి.
సాధన.
12 ÷ 3
12 – 3 = 9 → 1వ సారి
9 – 3 = 6 → 2వ సారి
6 – 3 = 3 → 3వ సారి
3 – 3 = 0 → 4వ సారి
12 ÷ 3 = 4
42 ÷ 7
42 – 7 = 35 → 1వ సారి
35 – 7 = 28 → 2వ సారి
28 – 7 = 21 → 3వ సారి
21 – 7 = 14 → 4వ సారి
14 – 7 = 7 → 5వ సారి
7 – 7 = 0 → 6వ సారి
కావున 42 ÷ 7 = 6
ప్రశ్న 2.
6 ÷ 0 మరియు 9 ÷ 0 సమానాలు అవుతాయా?
సాధన.
0 తో భాగహారం నిర్వచించబడదు. కావున 6 ÷ 0 మరియు 9 ÷ 0 సమానం అవుతాయని చెప్పలేము.
![]()
ప్రయత్నించండి [పేజి నెం. 22]
పూర్ణాంకాల సమితి వ్యవకలనం దృష్ట్యా స్థిత్యంతర ధర్మాన్ని పాటిస్తుందా?
సాధన.
6, 4 లు రెండు పూర్ణాంకాలు.
6 – 4 = 2 మరియు 4 – 6 = -2 పూర్ణాంకము కాదు.
కావున 6 – 4 ≠ 4 – 6
పూర్ణాంకాల సమితి వ్యవకలనం దృష్ట్యా స్థిత్యంతర ధర్మాన్ని పాటించదు.
పూర్ణాంకాల సమితి భాగహారం దృష్ట్యా స్థిత్యంతర ధర్మాన్ని పాటిస్తుందా?
సాధన.
6, 4 లు రెండు పూర్ణాంకాలు
6 ÷ 4 = \(\frac{6}{4}=\frac{3}{2}\) మరియు 4 ÷ 6 = \(\frac {2}{3}\) పూర్ణాంకము కాదు.
కావున 6 ÷ 4 ≠ 4 ÷ 6
కావున పూర్ణాంకాల సమితి భాగహారం దృష్ట్యా స్థిత్యంతర ధర్మాన్ని పాటించదు.
నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 23]
సరిచూడండి.
i) (5 × 6) × 2 = 5 × (6 × 2)
సాధన.
ఎడమచేతివైపు (L.H.S) = (5 × 6) × 2
= 30 × 2 = 60
కుడిచేతివైపు (R.H.S) = 5 × (6 × 2)
= 5 × 12 = 60
∴ L.H.S = R.H.S
కావున (5 × 6) × 2 = 5 × (6 × 2) సరైనదే.
ii) (3 × 7) × 5= 3 × (7 × 5)
సాధన.
ఎడమచేతివైపు (L.H.S) = (3 × 7) × 5
= 21 × 5 = 105
కుడిచేతివైపు (R.H.S) = 3 × (7 × 5)
= 3 × 35 = 105
∴ L.H.S = R.H.S
కావున (3 × 7) × 5 = 3 × (7 × 5) సరైనదే.
నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 24]
స్థిత్యంతర, సహచరధర్మాలను ఉపయోగించి కింది వాటిని సూక్ష్మీకరించండి.
అ) 319 + 69 +81
సాధన.
319 + 69 + 81 = 319 + (81 + 69) (స్థిత్యంతర ధర్మం )
= (319 +81) + 69 (సహచర ధర్మం )
= 400 + 69 = 469
ఆ) 431 + 37 + 69 + 63
సాధన.
431 + 37 + 69 + 63 = 431 + (37 + 69) + 63
= 431 + (69 + 37) + 63 (స్థిత్యంతర ధర్మం )
= (431 + 69) + (37 + 63) (సహచర ధర్మం )
= 500 + 100 = 600
ఇ) 2 × (71 × 5)
సాధన.
2 × (71 × 5) = 2 × (5 × 71) (స్థిత్యంతర ధర్మం )
= (2 × 5) × 71 (సహచర ధర్మం )
= 10 × 71 = 710
ఈ) 50 × 17 × 2
సాధన.
50 × (17 × 2) = 50 × (2 × 17) (స్థిత్యంతర ధర్మం)
= (50 × 2) × 17 (సహచర ధర్మం )
= 100 × 17 = 1700
![]()
ఆలోచించండి [పేజి నెం. 24]
(8 ÷ 2) ÷ 4 = 8 ÷ (2 ÷ 4) అవుతుందా ?
భాగహారానికి సహచరధర్మం వర్తిస్తుందా?
అలాగే వ్యవకలనానికి సహచరధర్మం వర్తిస్తుందేమో సరిచూడండి.
సాధన.
ఎడమచేతివైపు (L.H.S) = (8 ÷ 2) ÷ 4
= 4 ÷ 4 = 1
కుడిచేతివైపు (R.H.S) = 8 ÷ (2 ÷ 4)
= 8 ÷ (\(\frac {1}{2}\))
= 8 × 2 = 16
L.H.S ≠ R.H.S
కావున (8 ÷ 2) ÷ 4 = 8 ÷ (2 ÷ 4) కాదు.
అనగా భాగహారానికి సహచరధర్మం వర్తించదు.
ఇప్పుడు వ్యవకలనానికి సహచరధర్మం వర్తిస్తుందేమో ఒక ఉదాహరణతో పరిశీలిద్దాము.
(8 – 2) – 4 = 6 – 4 = 2
8 – (2 – 4) = 8 – (-2) = 8+ 2 = 10
∴ (8 – 2) – 4 ≠ 8 – (2 – 4)
కావున వ్యవకలనానికి సహచరధర్మం వర్తించదు.
[పేజి నెం. 24]
గుణకార విభాగ న్యాయం ఉపయోగించి కింది వాటిని సూక్ష్మీకరించండి.
అ) 2 × (5+ 6)
ఆ) 5 × (7 + 8)
ఇ) 19 × 7 + 19 × 3
సాధన.
అ) 2 × (5 + 6)
ఇచ్చినది 2 × (5 + 6) = (2 × 5) + (2 × 6)
సంకలనం మీద గుణకార విభాగన్యాయం ఉపయోగించి
2 × 11 = 10 + 12
22 = 22
L.H.S. = R.H.S
ఆ) 5 × (7 + 8)
ఇచ్చినది 5 × (7 + 8) = (5 × 7) + (5 × 8)
సంకలనం మీద గుణకార విభాగన్యాయం ఉపయోగించి
5 × 15 = 35 + 40
75 = 75
L.H.S : R.H.S
ఇ) 19 × 7 + 19 × 3
ఇచ్చినది (19 × 7) + (19 × 3) = 19 × (7 + 3)
సంకలనం మీద గుణకార విభాగన్యాయం ఉపయోగించి
133 + 57 = 19 × 10
190 = 190
L.H.S = R.H.S
![]()
ఇవి చేయండి [పేజి.నెం. 24]
అ) 25 × 78 ఆ) 17 × 26 ఇ) 49 × 68 + 32 × 49 విభాగ న్యా యాన్ని ఉపయోగించి కనుగొనండి.
సాధన.
అ) 25 × 78
(20 + 5) × 78 = (20 × 78) + (5 × 78) (విభాగ న్యా యం )
= 1560 + 390 = 1950
ఆ) 17 × 26 = 17 × (20 + 6)
= (17 × 20) + (17 × 6) (విభాగ న్యాయం)
= 340 + 102 = 442
ఇ) 49 × 68 + 32 × 49
= 49 × (68 + 32) (విభాగ న్యాయం)
= 49 × 100 = 4900
[పేజి నెం. 26]
కింది పట్టికను పూరించండి.
| సంఖ్య | రేఖ | దీర్ఘ చతురస్రం | చతురస్రం | త్రిభుజం |
| 2 | అవును | కాదు | కాదు | కాదు |
| 3 | అవును | కాదు | కాదు | అవును |
| 4 | అవును | కాదు | అవును | కాదు |
| 5 | ||||
| ….. | ||||
| 25 |
సాధన.
| సంఖ్య | రేఖ | దీర్ఘ చతురస్రం | చతురస్రం | త్రిభుజం |
| 2 | అవును | కాదు | కాదు | కాదు |
| 3 | అవును | కాదు | కాదు | అవును |
| 4 | అవును | కాదు | అవును | కాదు |
| 5 | అవును | కాదు | కాదు | కాదు |
| 6 | అవును | అవును | కాదు | అవును |
| 7 | అవును | కాదు | కాదు | కాదు |
| 8 | అవును | అవును | కాదు | కాదు |
| 9 | అవును | కాదు | అవును | కాదు |
| 10 | అవును | అవును | కాదు | అవును |
| 11 | అవును | కాదు | కాదు | కాదు |
| 12 | అవును | అవును | కాదు | కాదు |
| 13 | అవును | కాదు | కాదు | కాదు |
| 14 | అవును | అవును | కాదు | కాదు |
| 15 | అవును | అవును | కాదు | అవును |
| 16 | అవును | అవును | అవును | కాదు |
| 17 | అవును | కాదు | కాదు | కాదు |
| 18 | అవును | అవును | కాదు | కాదు |
| 19 | అవును | కాదు | కాదు | కాదు |
| 20 | అవును | అవును | కాదు | కాదు |
| 21 | అవును | అవును | కాదు | అవును |
| 22 | అవును | అవును | కాదు | కాదు |
| 23 | అవును | కాదు | కాదు | కాదు |
| 24 | అవును | అవును | కాదు | కాదు |
| 25 | అవును | కాదు | అవును | కాదు |
![]()
ప్రయత్నించండి [పేజి నెం. 27]
ప్రశ్న 1.
ఏ సంఖ్యలను రేఖగా మాత్రమే చూపవచ్చు ?
సాధన.
2, 3, 4, 5, 6, 7, ………… సంఖ్యలను రేఖగా చూపవచ్చు.
2 గాని అంతకన్నా ఎక్కువగాని సంఖ్యలు కలిసి రేఖను ఏర్పరుస్తాయి.
ప్రశ్న 2.
ఏఏ సంఖ్యలను దీర్ఘచతురస్రాలుగా చూపవచ్చు?
సాధన.
6, 8, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, ……… సంఖ్యలను దీర్ఘచతురస్రాలుగా చూపవచ్చును.
పై సంఖ్యలన్నీ సంయుక్త సంఖ్యలని గమనించగలము.
ప్రశ్న 3.
ఏఏ సంఖ్యలను చతురస్రాలుగా చూపవచ్చు?
సాధన.
4, 9, 16, 25, ………. సంఖ్యలను చతురస్రాలుగా చూపవచ్చును.
పై సంఖ్యలను రెండు సమాన సంఖ్యల లబ్ధంగా రాయవచ్చును.
4 = 2 × 2
9 = 3 × 3
16 = 4 × 4
25 = 5 × 5
పై సంఖ్యలు 4, 9, 16, 25, ……….. లు పరిపూర్ణ వర్గ సంఖ్యలు.
ప్రశ్న 4.
ఏఏ సంఖ్యలమ త్రిభుజాలుగా చూపవచ్చు?
సాధన.
3, 6, 10, 15, 21, …………. సంఖ్యలను త్రిభుజాలుగా చూపవచ్చును.
పై సంఖ్యలను మొదటి వరుస సహజ సంఖ్యల మొత్తంగా రాయవచ్చును.
3 = 1 + 2
6 = 1 + 2 + 3
0 = 1 + 2 + 3 + 4
15 = 1 + 2 + 3 + 4 + 5
21 = 1 + 2 + 3 + 4 + 5 + 6
పై సంఖ్యలను 3, 6, 10, 15, 21, ……….. త్రిభుజ సంఖ్యలు అంటారు.
![]()
ఉదాహరణలు
ప్రశ్న 1.
196 + 57 + 4 కనుగొనండి.
సాధన.
196 + (57 + 4)
= 196 + (4 + 57) [స్థిత్యంతర ధర్మం]
= (196 + 4) + 57 [సహచర ధర్మం]
= 200 + 57 = 257
ప్రశ్న 2.
5 × 9 × 2 × 2 × 3 × 5 ని కనుగొనండి.
సాధన.
5 × 9 × 2 × 2 × 3 × 5
= 5 × 2 × 9 × 2 × 5 × 3 [స్థిత్యంతర ధర్మం]
= (5 × 2) × 9 × (2 × 5) × 3 [సహచర ధర్మం]
= 10 × 9 × 10 × 3
= 90 × 30 = 2700
ప్రశ్న 3.
12 × 75 విభాగన్యాయాన్ని ఉపయోగించి కనుక్కోండి.
సాధన.
12 × 75 = 12 × (70 + 5) = 12 × (80 – 5)
= (12 × 70) + (12 × 5) లేదా = (12 × 80) – (12 × 5)
= 840 + 60 = 900 = 960 – 60 = 900