SCERT AP 6th Class Maths Solutions Chapter 3 గ.సా.కా – క.సా.గు Ex 3.5 Textbook Exercise Questions and Answers.
AP State Syllabus 6th Class Maths Solutions 3rd Lesson గ.సా.కా – క.సా.గు Exercise 3.5
ప్రశ్న 1.
కింద ఇవ్వబడిన సంఖ్యల గ.సా.భాను ప్రధాన కారణాంక విభజన పద్ధతి ద్వారా మరియు నిరంతర భాగహార పద్ధతి ద్వారా కనుగొనుము.
అ) 48, 64
ఆ) 126, 216
ఇ) 40, 60, 56
ఈ) 10, 35, 40
సాధన.
అ) 48, 64
ప్రధాన కారణాంక విభజన పద్ధతి :
\(\begin{array}{c|c}
2 & 48 \\
\hline 2 & 24 \\
\hline 2 & 12 \\
\hline 2 & 06 \\
\hline 3 & 3 \\
\hline & 1
\end{array}\)
\(\begin{array}{l|l}
2 & 64 \\
\hline 2 & 32 \\
\hline 2 & 16 \\
\hline 2 & 08 \\
\hline 2 & 4 \\
\hline 2 & 2 \\
\hline & 1
\end{array}\)
48 = 2 × 2 × 2 × 2 × 3
64 = 2 × 2 × 2 × 2 × 2 × 2
(48, 64)ల ఉమ్మడి కారణాంకాలు 2,2,2,2
∴ 48, 64 ల గ.సా.భా = 2 × 2 × 2 × 2 = 16
నిరంతర భాగహార పద్ధతి :

శేషం ‘0’ వచ్చినపుడు చివరి భాజకం 16.
∴ 48, 64 గ.సా.భా = 16
ఆ) 126, 216
ప్రధాన కారణాంక విభజన పద్ధతి :
\(\begin{array}{l|l}
2 & 126 \\
\hline 3 & 063 \\
\hline 3 & 21 \\
\hline 7 & 07 \\
\hline & 1
\end{array}\)
\(\begin{array}{l|r}
2 & 216 \\
\hline 2 & 108 \\
\hline 2 & 054 \\
\hline 3 & 27 \\
\hline 3 & 09 \\
\hline 3 & 3 \\
\hline & 1
\end{array}\)
126 = 2 × 3 × 3 × 7
216 = 2 × 2 × 2 × 3 × 3 × 3
126, 216 ల గ.సా.భా = 2 × 3 × 3 = 18
నిరంతర భాగహార పద్ధతి :
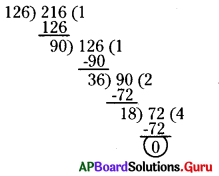
126, 216 ల గ.సా.భా = 18
ఇ) 40, 60, 56
ప్రధాన కారణాంక విభజన పద్ధతి :
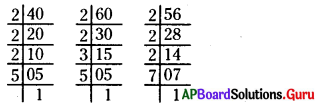
40 = 2 × 2 × 2 × 5
60 = 2 × 2 × 3 × 5
56 = 2 × 2 × 2 ×7
40,60,56 ల ఉమ్మడి కారణాంకాలు 2, 2
∴ 40,60,56 ల గ.సా.భా = 2 × 2 = 4
నిరంతర భాగహార పద్ధతి :

40, 60 ల గ.సా.భా = 20
ఇపుడు 20, 56 ల గ.సా.భా

20, 56 ల గ.సా.భా = 4
∴ 40, 60, 56 ల గ.సా.భా = 4
ఈ) 10, 35, 40
ప్రధాన కారణాంక విభజన పద్ధతి :
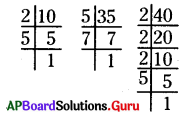
10 = 2 × 5
35 = 5 × 7
40 = 2 × 2 × 2 × 5
ఉమ్మడి కారణాంకం = 5
10, 35, 40 ల గ.సా.భా = 5
నిరంతర భాగహార పద్ధతి :
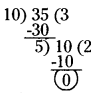
10, 35 ల గ.సా.భా = 5

5, 40 ల గ.సా.భా = 5
∴ 10, 35, 40 ల గ.సా.భా = 5.
![]()
ప్రశ్న 2.
రెండు పాలక్యాన్లలో వరుసగా 60 లీటర్లు, 165 లీటర్ల పాలు ఉన్నవి. రెండు క్యాన్లలోని పాలను కొలవగలిగే గరిష్ఠ పరిమాణం కలిగిన క్యానను కనుగొనండి.
సాధన.
రెండు పాలక్యాన్లలో గల పాలు = 60 లీటర్లు మరియు 165 లీటర్లు
రెండు క్యాన్లలోని పాలను కొలవగలిగే గరిష్ఠ పరిమాణం కలిగిన క్యాన్ = 60, 165 ల గ.సా.భా.
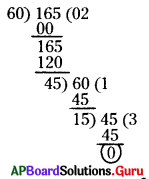
60, 165 ల గ.సా.భా = 15
∴ పాలను కొలవగలిగే గరిష్ఠ పరిమాణం కలిగిన క్యాన్ = 15 లీటర్లు.
ప్రశ్న 3.
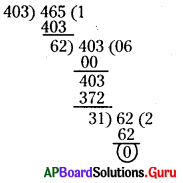
మూడు వేర్వేరు కొలతలు గల కంటైనర్లలో వరుసగా 403 లీటర్లు, 465 లీటర్లు, 527 లీటర్లు పరిమాణాలలో పాలు ఉన్నవి. వేర్వేరు పరిమాణాలలో గల కంటైనర్లలోని పాలను పూర్తిగా కొలవగలిగే గరిష్ఠ పరిమాణం గల కొలత ఎంత?
సాధన.
మూడు కంటైనర్లలో గల పాల పరిమాణం = 403 లీటర్లు, 465 లీటర్లు, 527 లీటర్లు
కంటైనర్లలోని పాలను పూర్తిగా కొలవగలిగే
గరిష్ట పరిమాణం గల కొలత = 403, 465, 527 ల గ.సా.భా = 31