SCERT AP 6th Class Maths Solutions Chapter 3 గ.సా.కా – క.సా.గు Ex 3.6 Textbook Exercise Questions and Answers.
AP State Syllabus 6th Class Maths Solutions 3rd Lesson గ.సా.కా – క.సా.గు Exercise 3.6
1. ప్రధాన కారణాంక విభజన పద్ధతి ప్రకారం కింది సంఖ్యల క.సా.గును కనుగొనండి.
అ) 12 మరియు 15
అ) 15 మరియు 25
ఇ) 14 మరియు 21
సాధన.
అ) 12 మరియు 15
\(\begin{array}{l|l}
2 & 12 \\
\hline 2 & 6 \\
\hline 3 & 3 \\
\hline & 1
\end{array}\)
\(\begin{array}{l|l}
3 & 15 \\
\hline 5 & 5 \\
\hline & 1
\end{array}\)
12 = 2 × 2 × 3; 15 = 3 × 5
ఉమ్మడి కారణాంకాలు = 3
మిగిలిన కారణాంకాలు = 2 × 2 × 5
∴ 12 మరియు 15 ల క.సా.గు = ఉమ్మడి కారణాంకాలు × మిగిలిన కారణాంకాలు = 3 × 2 × 2 × 5 = 60
ఆ) 15 మరియు 25
\(\begin{array}{l|l}
3 & 15 \\
\hline 5 & 5 \\
\hline & 1
\end{array}\)
\(\begin{array}{c|c}
5 & 25 \\
\hline 5 & 5 \\
\hline & 1
\end{array}\)
15 = 3 × 5; 25 = 5 × 5
ఉమ్మడి కారణాంకాలు = 5
మిగిలిన కారణాంకాలు = 3 × 5
∴ 15 మరియు 25 ల క.సా.గు = 5 × 3 × 5 = 75
ఇ) 14 మరియు 21
\(\begin{array}{l|l}
2 & 14 \\
\hline 7 & 7 \\
\hline & 1
\end{array}\)
\(\begin{array}{l|l}
3 & 21 \\
\hline 7 & 7 \\
\hline & 1
\end{array}\)
14 = 2 × 7; 21 = 3 × 7
ఉమ్మడి కారణాంకాలు = 7
మిగిలిన కారణాంకాలు = 2 × 3
14 మరియు 21 ల క.సా.గు = 7 × 2 × 3 = 42
![]()
2. భాగహార పద్ధతిని ఉపయోగించి కింది సంఖ్యల క.సా.గును కనుగొనండి.
అ) 84, 112, 196
ఆ) 102, 119, 153
ఇ) 45, 99, 132, 165
సాధన.
అ) 84, 112, 196

∴ 84, 112, 196 ల క.సా.గు = 2 × 2 × 7 × 3 × 4 × 7 = 2352
ఆ) 102, 119, 153

102, 119, 153 ల క.సా.గు = 3 × 17 × 2 × 7 × 3 = 2142
ఇ) 45, 99, 132, 165
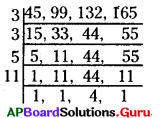
45, 99, 132, 165 ల క.సా.గు
= 3 × 3 × 5 × 11 × 4 = 1980
3. ఏ కనిష్ఠ సంఖ్యను 5 కు కలిపిన అది 12, 14 మరియు 18 ల చేత నిశ్శేషంగా భాగించబడునో కనుగొనండి.
సాధన.
12, 14 మరియు 18 ల క.సా.గు

2 × 3 × 2 × 7 × 3 = 252
252 – 5 = 247
12, 14 మరియు 18 ల చేత నిశ్శేషంగా భాగింపబడుటకు 5 కు కలపవలసిన కనిష్ఠ సంఖ్య = 247.
4. ఏ గరిష్ఠ మూడంకెల సంఖ్యను 75, 45 మరియు 60 లచే భాగిస్తే
అ) శేషం సున్న వస్తుంది. ఆ) శేషం ప్రతి సందర్భంలో 4 వచ్చును.
సాధన.
75, 45 మరియు 60 ల క.సా.గు
= 3 × 5 × 5 × 3 × 4 = 900
(900 కన్న పెద్దది మరియు 75, 45, 60 లతో భాగింపబడే సంఖ్య = 900 × 2 = 1800 కాని ఇది నాలుగంకెల సంఖ్య)

అ) 75, 45, 60 లచే భాగిస్తే శేషం ‘0’ వచ్చే గరిష్ఠ మూడంకెల సంఖ్య = 900
ఆ) శేషం ప్రతి సందర్భంలోను 4 వచ్చే గరిష్ఠ మూడంకెల సంఖ్య = 900 + 4 = 904
![]()
5. రెండు గంటలు వరుసగా 3 నిమిషాలు మరియు 4 నిమిషాలకు మోగుతాయి. ఒకసారి రెండు గంటలు కలిసి మోగిన తర్వాత, తిరిగి అవి రెండూ కలిసి మోగడానికి ఎంత సమయం పడుతుంది?
సాధన.
3, 4 ల క.సా.గు = 2 × 2 × 3 = 12

ఒకసారి రెండు గంటలు కలిసి మోగిన తర్వాత, తిరిగి అవి రెండూ కలిసి మోగడానికి 12 నిమిషాల సమయం పడుతుంది.