AP State Syllabus AP Board 6th Class Maths Solutions Chapter 3 HCF and LCM Ex 3.7 Textbook Questions and Answers.
AP State Syllabus 6th Class Maths Solutions 3rd Lesson HCF and LCM Ex 3.7
Question 1.
Find the LCM and HCF of the following numbers and check their relationship.
i) 15, 24
ii) 8, 25
iii) 12, 48
iv) 30, 48
Answer:
i) 15,24
The given numbers are 15 and 24.
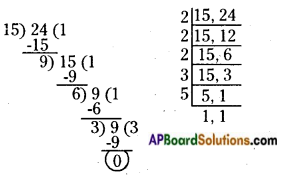
LCM of 15 and 24 = 2 × 2 × 2 × 3 × 5 = 120
HCF of 15 and 24 = 3
Now, LCM × HCF = 120 × 3 = 360
Product of two numbers = 15 × 24 = 360,
∴ LCM × HCF = Product of the numbers.
![]()
ii) 8,25
The given numbers are 8 and 25.
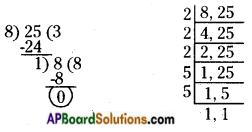
LCM of 8 and 25 = 2 × 2 × 2 × 5 × 5 = 200
HCF of 8 and 25 = 1
Now LCM × HCF = 200 × 1 = 200
Product of two numbers = 8 × 25 = 200
∴ LCM × HCF = Product of the numbers
iii) 12, 48
The given numbers are 12 and 48.
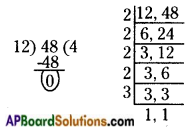
LCM of 12 and 48 = 2 × 2 × 2 × 2 × 3 = 48
HCF of 12 and 48 = 12
Now LCM × HCF = 48 × 12 = 576
Product of two numbers = 12 × 48 = 576
∴ LCM × HCF = Product of the numbers
iv) 30, 48
Given numbers are 30 and 48.

LCM of 30 and 48 = 2 × 2 × 2 × 2 × 3 × 5 = 240
HCF of 30 and 48 = 6
LCM × HCF = 240 × 6 = 1440
Product of the numbers = 30 × 48 = 1440
∴ LCM × HCF = Product of the numbers.
![]()
Question 2.
If the LCM of two numbers is 290 and their product is 7250, what will be its HCF?
Answer:
Given LCM of two numbers = 290
Product of two numbers = 7250
HCF of two numbers = ?
We know that, LCM × HCF = Product of two numbers
290 × HCF = 7250
HCF = \(\frac{7250}{290}\) = 25
∴ HCF of two numbers = 25
Question 3.
The product of two numbers is 3276. If their HCF is 6, find their LCM.
Answer:
Given HCF of two numbers = 6
Product of two numbers = 3276
LCM of two numbers = ?
We know that, LCM × HCF = Product of two numbers
LCM × 6 = 3276
LCM = \(\frac{3276}{6}\) = 546
∴ LCM of two numbers = 546
Question 4.
The HCF of two numbers is 6 and their LCM is 36. If one of the numbers is 12, find the other.
Answer:
Given LCM of two numbers = 36
HCF of two numbers = 6
One of the numbers a = 12
Let second number b = ?
We know that, product of two numbers = LCM × HCF
a × b = LCM × HCF
12 × b = 36 × 6
b = \(\frac{36 × 6}{12}\) = 18
∴ Second number b = 18
Question 5.
Can two numbers have 16 as their HCF and 384 as their LCM? Give reason.
Answer:
Here, if we divide 384 by 16
\(\frac{384}{16}\) = 24 (No remainder)
If HCF is the factor LCM of two numbers, then it is possible.
![]()
Question 6.
Can two numbers have 14 as their HCF and 204 as their LCM? Give reasons in support of your answer.
Answer:
Here, if we divide 204 by 14
\(\frac{204}{14}\) = 14 and the remainder is 8.
HCF is not the factor of LCM to two numbers. So, it is not possible.