Students can go through AP Board 8th Class Maths Notes 1st Lesson అకరణీయ సంఖ్యలు to understand and remember the concept easily.
AP Board 8th Class Maths Notes 1st Lesson అకరణీయ సంఖ్యలు
→ p, q లు పూర్ణసంఖ్యలయి, q ≠ 0 అయితే \(\frac{p}{q}\) రూపంలో రాయగల సంఖ్యలను అకరణీయ సంఖ్యలు అంటారు. అకరణీయ సంఖ్యా సమితిని ‘Q’ అనే అక్షరంచే సూచిస్తారు.
Q = {x/x ∈ \(\frac{p}{q}\),q ≠ 0}
→ అకరణీయ సంఖ్యలు సంకలనం, వ్యవకలనం దృష్ట్యా సంవృత ధర్మాన్ని పాటిస్తాయి.
→ అకరణీయ సంఖ్యలు గుణకారం దృష్ట్యా సంవృత ధర్మాన్ని పాటిస్తాయి. కానీ భాగహారం దృష్ట్యా సంవృత ధర్మాన్ని పాటించవు.
![]()
→ పూర్ణాంకాలు :
| పరిక్రియలు | ఉదాహరణలు | వ్యాఖ్య |
| సంకలనం | 2, 3 లు పూర్ణాంకాలు 2 + 3 = 5 మరియు 3 + 2 = 5 ∴ 2 + 3 = 3 + 2 | పూర్ణాంకాలు సంకలనం దృష్ట్యా వినిమయ ధర్మాన్ని పాటిస్తాయి. |
| వ్యవకలనం | 3 – 2 మరియు 2 – 3 లు సమానమేనా ? కాదు | వ్యవకలనం దృష్ట్యా స్థిత్యంతర ధర్మాన్ని పాటించవు. |
| గుణకారము | 3 × 2 = 2 × 3 = 6 | గుణకారం దృష్ట్యా స్థిత్యంతర ధర్మాన్ని పాటిస్తాయి. |
| భాగహారము 4 + 2 = ? 2 : 4 = ? 4 |
2, 2 + 4 లు సమానమేనా ? కాదు | భాగహారం దృష్ట్యా స్థిత్యంతర ధర్మాన్ని పాటించవు. |
→ పూర్ణాంకాలు :
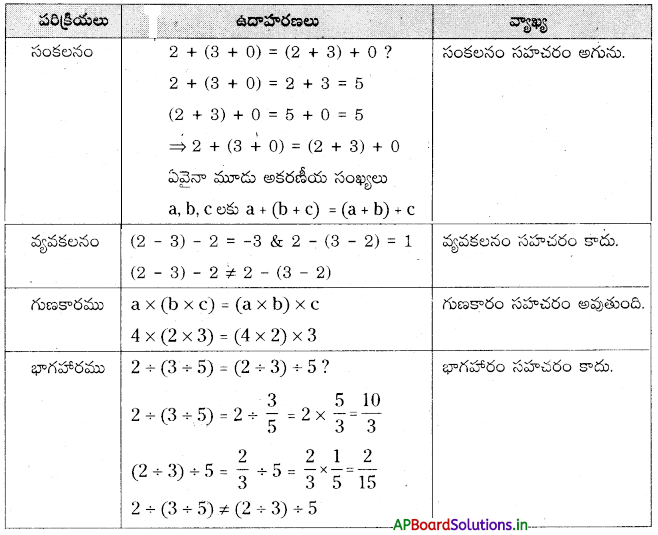
→ a యొక్క సంకలన విలోమం = – a [∵ a + (-a) = 0 ]
→ a యొక్క గుణకార విలోమం = \(\frac{1}{a}\) [a × \(\frac{1}{a}\) = 1]
→ ‘0’ అకరణీయ సంఖ్యల సంకలన తత్సమాంశం.
→ 1 అకరణీయ సంఖ్యల గుణకార తత్సమాంశం.
→ ఒక అకరణీయ సంఖ్య మరియు దాని సంకలన విలోమములు వ్యతిరేక గుర్తులు కలిగి ఉంటాయి.
→ ఒక కరణీయ సంఖ్య లవహారాలను తారుమారు చేయగా (వ్యుతమం చేయగా) లభించేది దాని గుణకార విలోమం.
→ విభాగన్యాయం : a, b, c లు ఏవైనా మూడు అకరణీయ సంఖ్యలు అయితే a(b + C) = ab + ac మరియు a (b – C) = ab – ac
![]()
→ ప్రతి అకరణీయ సంఖ్యను సంఖ్యారేఖ పై చూపవచ్చు.
→ ఏవైనా రెండు అకరణీయ సంఖ్యల మధ్య అనంతమైన అకరణీయ సంఖ్యలు ఉండును. రెండు అకరణీయ సంఖ్యల మధ్య మరో అకరణీయ సంఖ్యను ఉంచటానికి సగటు భావన ఉపయోగపడుతుంది.
→ ఒక అకరణీయ సంఖ్యను అంతంగల దశాంశంగాను లేదా అంతం లేని ఆవర్తిత దశాంశంగాను వ్రాయవచ్చు.