AP SCERT 6th Class Maths Textbook Solutions Chapter 7 బీజ గణిత పరిచయం InText Questions and Answers.
AP State Syllabus 6th Class Maths Solutions 7th Lesson బీజ గణిత పరిచయం InText Questions
ప్రయత్నించండి [పేజి నెం. 107, 108]
ప్రశ్న 1.
రెండు అగ్గిపుల్లలను అమర్చి పక్క అమరికను ఏర్పరచండి.

ఇలాంటి రూపాలు 2సార్లు, 3సార్లు, 4సార్లు ఏర్పరచి, ఈ అమరికకు తగిన సూత్రంను కనుగొనండి.
సాధన.
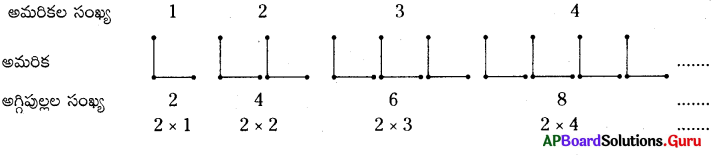
సూత్రం : n వ అమరికకు కావలసిన అగ్గిపుల్లల సంఖ్య = 2 × n = 2n
![]()
ప్రశ్న 2.
రీటా అగ్గిపుల్లలతో పక్క అమరికను ఏర్పరచింది. ఆమె దీనిని కొనసాగించి కావలసిన అగ్గిపుల్లల సంఖ్య = 6y, y అనునది ఏర్పరచబడే పక్కరూపాలు అనే నియమం కనుగొన్నది? దీనిని నీవు అంగీకరిస్తావా? వివరిస్తూ, ఇలాంటి 5 అమరికలను ఏర్పరచటానికి కావలసిన అగ్గిపుల్లల సంఖ్యను కనుగొనండి.

సాధన.
రీటా కనుగొన్న నియమంతో ఏకీభవిస్తాను.
వివరణ:
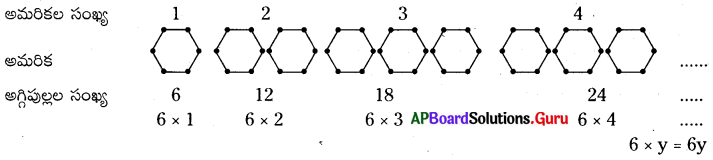
సూత్రం : 5 అమరికలను ఏర్పరచటానికి కావలసిన అగ్గిపుల్లల సంఖ్య = 5 × 6 = 30
6 × y = 6y
ప్రశ్న 3.
కింది ఆకారాలను అమర్చడానికి అగ్గిపుల్లల సంఖ్యను పరిశీలించండి.
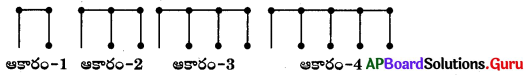
(i) పై అమరికలో ప్రతీ ఆకారాల సమూహానికి కావలసిన అగ్గిపుల్లల సంఖ్యకు సూత్రం కనుగొనండి.
(ii) పై విధంగా ఉండే12 ఆకారాల సమూహాల అమరికకు కావలసిన అగ్గిపుల్లల సంఖ్యను తెల్పండి.
సాధన.
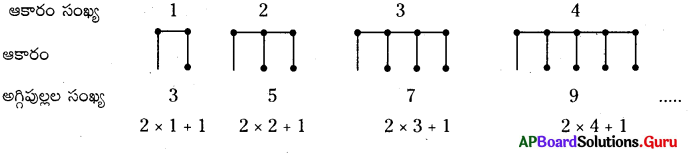
(i) సూత్రం : n వ ఆకారంలో అగ్గిపుల్లల సంఖ్య = 2 × n + 1
(ii) 12 ఆకారాల సమూహాల అమరికకు కావలసిన అగ్గిపుల్లల సంఖ్య = 2 × 12 + 1 = 24 + 1 = 25.
![]()
నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 110]
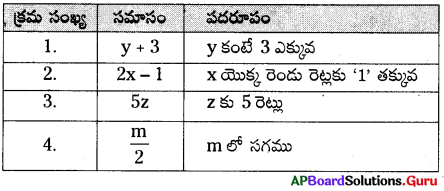
ఇచ్చిన ఉదాహరణ ప్రకారం కింది పట్టికలో మిగిలిన వాటిని రాయండి.
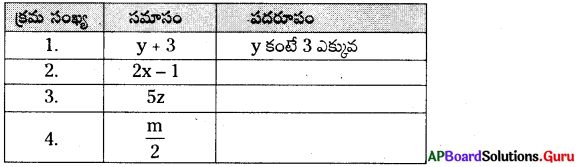
సాధన.
ప్రయత్నించండి [పేజి నెం. 111]
ప్రశ్న 1.
దీర్ఘచతురస్ర చుట్టుకొలత కనుక్కోవడానికి సాధారణ సూత్రం కనుగొనండి. (పొడవుకు ‘l’, వెడల్పుకు ‘b’ అనే చరరాశులను తీసుకోండి)
సాధన.
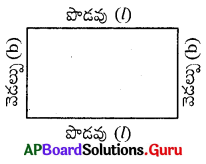
దీర్ఘచతురస్రము చుట్టుకొలత
= పొడవు + వెడల్పు + పొడవు + వెడల్పు
= 2 పొడవులు + 2 వెడల్పులు
= 2l + 2b (ఇక్కడ పొడవును l, వెడల్పును b గా తీసుకొన్నాము)
= 2(l + b) (విభాగన్యాయం)
∴ దీర్ఘచతురస్ర చుట్టుకొలత = 2(l + b)
![]()
ప్రశ్న 2.
చతురస్ర వైశాల్యం కనుగొనడానికి సాధారణ సూత్రం రాయండి. (చతురస్ర భుజాన్ని 8 అనే చరరాశితో గుర్తించండి)
సాధన. చతురస్ర వైశాల్యం = భుజం × భుజం
= s × s (చతురస్రభుజాన్ని S గా గుర్తించాము)
పేజి నెం. 112
1. కింది సంఖ్యల అమరికకు nవ పదం రాయండి.
ప్రశ్న (అ)
3, 6, 9, 12, ………….
సాధన.
ఇవ్వబడిన సంఖ్యల అమరిక 3, 6, 9, 12, ……………….

మొదటి సంఖ్య = 3 × 1
రెండవ సంఖ్య = 3 × 2
‘n’ వ సంఖ్య : 3 × n = 3n
కావున, 3, 6, 9, 12, …….. అమరికలో ‘n’ వ పదం = 3n
ప్రశ్న (ఆ)
2, 5, 8, 11, …………..
సాధన.
ఇవ్వబడిన సంఖ్యల అమరిక 2, 5, 8, 11, ……

మొదటి సంఖ్య = 2 = 3 × 1 – 1
రెండవ సంఖ్య = 5 = 3 × 2 – 1
మూడవ సంఖ్య = 8 = 3 × 3 – 1
‘n’ వ సంఖ్య = n = 3 × n – 1 = 3n – 1
కావున, 2, 5, 8, 11, ….. అమరికలో ‘n’ వ పదం = 3n – 1
![]()
ప్రశ్న (ఇ)
21, 4, 9, 16, …………
సాధన.
ఇవ్వబడిన సంఖ్యల అమరిక 1, 4, 9, 16, …….

మొదటి సంఖ్య = 1 = 1 × 1
రెండవ సంఖ్య = 4 = 2 × 2
మూడవ సంఖ్య = 9 = 3 × 3
‘n’వ సంఖ్య = n = n × n = n2
కావున, 1, 4, 9, 16….. అమరికలో ‘n’ వ పదం = n2
నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 113]
ప్రశ్న 1.
కింది పట్టికను పూర్తిచేసి \(\frac {P}{3}\) = 4 అనే సమీకరణంను సంతృప్తి పరిచే ‘p’.
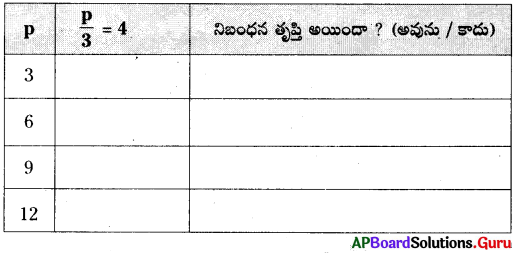
సాధన.
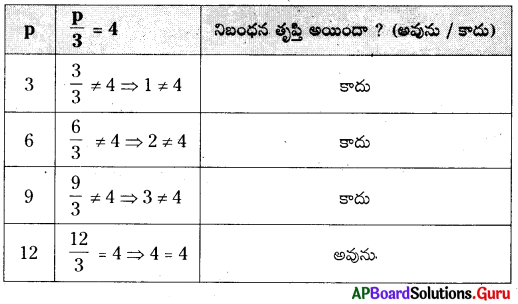
\(\frac {P}{3}\) = 4 అనే సమీకరణంను సంతృప్తిపరిచే p విలువ = 12
2. కింది సమీకరణాలలో LHS మరియు RHS లను గుర్తించి, రాయండి.
ప్రశ్న (అ)
2x + 1 = 10
సాధన.
2x + 1 = 10
L.H.S = 2x + 1
R.H.S = 10
![]()
ప్రశ్న (ఆ)
9 = y – 2
సాధన.
9 = y – 2
LHS = 9
RHS = y – 2
ప్రశ్న (ఇ)
3p + 5 = 2p + 10
సాధన.
LHS = 3p + 5
RHS = 2p + 10
ప్రశ్న 3.
ఏవైనా రెండు సామాన్య సమీకరణాలు రాసి, వాటి యొక్క LHS మరియు RHS లను తెలపండి.
సాధన.
(i) 3x + 4 = 19
L.H.S = 3x + 4
RHS = 19
(ii) 8 = 7y – 6
LHS = 8
RHS = 7y – 6
![]()
ప్రయత్నించండి [పేజి నెం. 114]
ప్రశ్న 1.
3m = 15 అనే సమీకరణాన్ని పరిశీలించి, m అనే చరరాశి యొక్క ఏ విలువకు సమీకరణంలో LHS మరియు RHS లు సమానమైనాయో చూడండి.
సాధన.
m = 5 అయినప్పుడు ఇచ్చిన సమీకరణంలో LHS మరియు RHS లు సమానం అవుతాయి.
∴ 3m = 15 సమీకరణ సాధన m = 5.
ఉదాహరణలు
ప్రశ్న 1.
రాము వద్ద రహీం వద్ద కన్నా 3 పెన్సిళ్ళు ఎక్కువ ఉన్నాయి. రహీం వద్ద గల పెన్సిళ్లను బట్టి రాము వద్ద గల పెన్సిళ్ల సంఖ్యకు సూత్రం రాయండి.
సాధన.
రహీం వద్ద 2 పెన్సిళ్లు ఉంటే రాము వద్ద ఉండేవి 2 + 3 = 5 పెన్సిళ్లు.
రహీం వద్ద 5 పెన్సిళ్లు ఉంటే రాము వద్ద ఉండేవి 5 + 3 = 8 పెన్సిళ్లు.
రహీం వద్ద ఎన్ని పెన్సిళ్లున్నవో తెలియదు.
కాని మనకు తెల్సింది రాముని వద్ద గల పెన్సిళ్లు = రహీం పెన్సిళ్లు + 3
అందుచే రహీం వద్దగల పెన్సిళ్ల సంఖ్యను ‘n’ అనుకుంటే రాము వద్ద గల పెన్సిళ్ల సంఖ్య = n + 3 అగును.
ఇచ్చట n = 1, 2, 3, …………… అగును. అందుచే ‘n’ అనేది ఒక చరరాశి.
ప్రశ్న 2.
హేమ, మాధవి ఇద్దరు అక్కచెల్లెళ్లు. మాధవి, హేమకన్నా 3 సంవత్సరాలు చిన్నది. మాధవి వయస్సును, హేమ వయస్సుతో పోల్చి సూత్రం రాయండి.
సాధన.
మాధవి, హేమకన్నా 3 సంవత్సరాలు ‘చిన్నది’ అని ఇవ్వబడింది.
హేమ వయస్సు 10 సంవత్సరాలు అయితే మాధవి వయస్సు 10 – 3 = 7 సంవత్సరాలు.
హేమ వయస్సు 16 సంవత్సరాలు అయితే మాధవి వయస్సు 16 – 3 = 13 సంవత్సరాలు.
హేమ వయస్సు కచ్చితంగా తెలియనప్పుడు, ఏ వయస్సును తీసుకున్ననూ, మాధవి వయస్సు తెలుసుకోవాలి.
హేమ వయస్సు ‘p’ సంవత్సరాలు అయితే మాధవి వయస్సు “p – 3” సంవత్సరాలు అగును.
ఇచ్చట ‘p’ అనేది చరరాశికి ఉదాహరణ. దీనికి 3, 4, 5, …… వంటి విలువలు ఇస్తాం.
దీని నుండి ‘p’ = 10 అయిన ‘p – 3’ = 7 అయిన p = 16 అయితే p – 3 = 13 అని తెలుస్తుంది.
![]()
ప్రశ్న 3.
కింది సమాసాలకు వాక్యాలను రాయండి.
(i) 2p
(ii) 7 + x
సాధన.
(i) సీమ వద్ద ఉన్న డబ్బుకు రెట్టింపు డబ్బు రాజు వద్ద ఉంది.
(ii) దిలిప్ వద్ద కంటే నా వద్ద 7 గోళీలు ఎక్కువగా ఉన్నాయి.
ప్రశ్న 4.
మనోజ్ చిక్కుడు విత్తనాల కన్నా, వేరుశనగ విత్తనాలను 5 ఎక్కువగా నాటాడు. అయిన వేరుశనగ విత్తనాలు ఎన్ని?
సాధన.
నాటిన చిక్కుడు విత్తనాలు = m అనుకొనండి. అందుచే నాటిన వేరుశనగ విత్తనాల సంఖ్య = ‘m + 5’ అగును.