AP State Syllabus AP Board 6th Class Maths Solutions Chapter 7 Introduction to Algebra InText Questions and Answers.
AP State Syllabus 6th Class Maths Solutions 7th Lesson Introduction to Algebra InText Questions
![]()
Let’s Explore (Page No. 102)
Question 1.
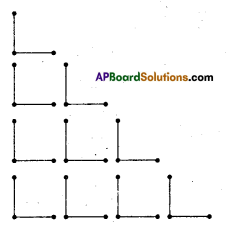
Arrange 2 matchsticks to form the shape 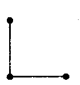 Continue the same shape for 2 times, 3 times and 4 times. Frame the rule for repeating the pattern.
Continue the same shape for 2 times, 3 times and 4 times. Frame the rule for repeating the pattern.
Solution:
To make the given shape 2 matchsticks are needed.
To make the given 2 shapes 4 matchsticks are needed.
To make the given 3 shapes 6 matchsticks are needed.
To make the given 4 shapes 8 matchsticks are needed.
Continue and arrange the information in the following table.

Number of matchsticks required = 2 × Number of shapes to be formed
= 2 × x = 2x
Question 2.
Rita took matchsticks to form the shape
She repeated the pattern and gave a rule.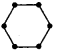
Number of matchsticks needed = 6.y, where y is the number of shapes to be formed. Is it correct ? Explain.
What is the number of sticks needed to form 5 such shapes ?
Solution:
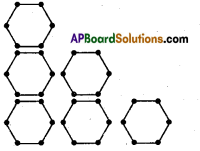
To make the given shape 6 matchsticks are needed.
To make the given 2 shapes 12 matchsticks are needed.
To make the given 3 shapes 18 matchsticks are needed.
Continue and arrange the information in the following table.

Yes, it is correct.
Number of matchsticks required = 2 × Number of shapes to be formed
= 2 × y = 2y
Number of matchsticks needed to form 5 such shapes = 6 × 5 = 30
Let’s Explore (Page No. 103)
Question 1.
A line of shapes is constructed using matchsticks.

Shape-1 Shape-2 Shape-3 Shape-4
i) Find the rule that shows how many sticks are needed to make a line of such shapes ?
ii) How many matchsticks are needed to form shape -12 ?
Solution:

Number of matchsticks 3 5 7 9
i) Let us know the pattern
S1 = 3 = 2 + 1 = (1 × 2) + 1
S2 = 5 = 4 + 1 = (2 × 2) + 1
S3 = 7 = 6 + 1 = (3 × 2) + 1
S4 – 9 = 8 + 1 = (4 × 2) + 1
Now the rule for this pattern is number of matchsticks.
ii) Used to make ‘n’ number of shapes is Sn = (n × 2) + 1 = 2n + 1
Number of matchsticks needed to form shape – 12 is
S12 = 2(12) + 1 = 24 + 1 = 25 sticks.
Check Your Progress (Page No. 105)
Question 1.
Fill the following table as instructed. One is shown for you.
| S.No. | Expression | Verbal Form |
| 1. | y + 3 | Three more than y |
| 2. | 2x – 1 | |
| 3. | 5z | |
| 4. | \(<table border=”2″>\) |
Solution:
| S.No. | Expression | Verbal Form |
| 1. | y + 3 | Three more than y |
| 2. | 2x – 1 | One less than the double of x |
| 3. | 5z | 5 times of z |
| 4. | \(<table border=”2″>\) | Half of the m |
Let’s Explore ? (Page No. 106)
Question 1.
Find the general rule for the perimeter of a rectangle. Use variables T and ‘b’ for length and breadth of the rectangle respectively.
Solution:
Given length of rectangle = l
breadth of rectangle = b
We know that the perimeter of rectangle is twice the sum of its length and breadth.
Sum of length and breadth = l + b
Twice the sum of length and breadth = 2 × (l + b)
Rule for the perimeter of a rectangle = 2(l + b)
Question 2.
Find the general rule for the area of a square by using the variable ‘s’ for the side of a square.
Answer:
Given side of a square = s
We know that the area of a square is the product of side and side.
Area of a square = side × side
Rule for the area of a square = s.s
| Side | Area |
| 1 | 1 × 1 |
| 2 | 2 × 2 |
| 3 | 3 × 3 |
| 4 | 4 × 4 |
| ……….. | ………… |
| s | S × s |
(Page No. 107)
Question 1.
Find the nth term in the following sequences.
0 3, 6, 9, 12, ii) 2, 5, 8, 11, iii) 1, 4, 9, 16,
Solution:
i) Given number pattern is 3, 6, 9, 12,……………..
To find the nth term in the given pattern, we put the sequence in a table.

First number = 3 × 1
Second number = 3 × 2
nth number = 3 × n = 3n
So, the nth term of the pattern 3, 6, 9, 12, is 3n.
ii) Given number pattern is 2, 5, 8, 11,
To find the nth term in the given pattern, we put the sequence in a table.

First number = 2 = 3 × 1 – 1
Second number = 5 = 3 × 2 – 1
Third number = 8 = 3 × 3 – 1
nth number = 3 × n – 1 = 3n – 1
So, the nth term of the pattern 2, 5, 8, 11 is 3n – 1.
iii) Given number pattern is 1, 4, 9, 16,
To find the nth term in the given pattern, we put the sequence in a table.

First number =1 = 1 × 1
Second number = 4 = 2 × 2
Third number =9 = 3 × 3
nth number = n × n = n2
So, the nth term of the pattern 1, 4, 9, 16 is n2.
Check Your Progress (Page No. 108)
Question 1.
Complete the table and find the value of ‘p’ for the equation \(\frac{\mathbf{p}}{\mathbf{3}}\) = 4
| p | \(\frac{\mathbf{p}}{3}\) = 4 | Condition satisfied ? Yes/ No |
| 3 | ||
| 6 | ||
| 9 | ||
| 12 |
Solution:
| p | \(\frac{\mathbf{p}}{3}\) = 4 | Condition satisfied ? Yes/ No |
| 3 | \(\frac{3}{3}\) ≠1 ≠ 4 | No |
| 6 | \(\frac{6}{3}\) ≠2 ≠ 4 | No |
| 9 | \(\frac{9}{3}\) ≠ 3 ≠ 4 | No |
| 12 | \(\frac{12}{3}\) ≠ 4 ≠ 4 | Yes |
Question 2.
Write LHS and RHS of following simple equations.
i) 2x + 1 = 10
ii) 9 = y – 2
iii) 3p + 5 = 2p + 10
Solution;
i) 2x+ 1 = 10
Given equation is 2x + 1 = 10
L.H.S = 2x + 1
R.H.S = 10
ii) 9 = y – 2
Given equation is 9 = y – 2
LHS = 9
RHS = y – 2
iii) 3p + 5 = 2p + 10
Given equation is 3p + 5 = 2p + 10
LHS = 3p + 5
RHS = 2p + 10
Question 3.
Write any two simple equations and write their LHS and RHS.
Solution:
i) Consider 8x + 3 = 4 is a simple equation.
L.H.S = 8x + 3
RHS = 4
ii) Consider 5a + 6 = 8a – 3 is a simple equation.
LHS = 5a + 6
RHS = 8a – 3
Let’s Explore (Page No. 109)
Observe for what value of m, the equation 3m = 15 has both LHS and RHS become equal.
Solution:
Given equation is 3m = 15
If m = 1, then the value of 3m = 3(1) = 3≠15 ∴ LHS ≠RHS
If m = 2, then the value of 3m = 3(2) = 6 ≠ 15 ∴ LHS ≠ RHS
If m = 3, then the value of 3m = 3(3) = 9≠15 ∴ LHS ≠ RHS
If m = 4, then the value of 3m = 3(4) = 12 ≠ 15 ∴ LHS ≠ RHS
If m = 5, then the value of 3m = 3(5) = 15 = 15 ∴ LHS = RHS
From the above when m = 5 the both LHS and RHS are equal