Students can go through AP Board 7th Class Maths Notes Chapter 6 Ratio – Applications to understand and remember the concepts easily.
AP State Board Syllabus 7th Class Maths Notes Chapter 6 Ratio – Applications
→ Ratio: A ratio is an ordered comparison of quantities of the same units.
We use the symbol ‘:’ to represent a ratio. The ratio of two quantities ‘a’ and ‘b’ is a : b and we read it as “a is to b”. The two quantities ‘a’ and ‘b’ are called the terms of the ratio. The first quantity ‘a’ is called first term or antecedent and the second quantity ‘b’ is called consequent.
→ Proportion: If two ratios are equal, then the four terms of the ratios are said to be in proportion. We use the symbol : : (is as)
If two ratios a : b and c : d are equal, we write a : b :: c : d or a : b = c : d
Here ‘a’, ‘d’ are called extremes and b, c are called means.
![]()
→ Unitary Method: The method in which we first find the value of one unit and then the value of the required number of units is known as unitary method.
Eg: If the cost of 5 pens is Rs. 85; then the cost of 12 pens is ……… ?
Solution. Cost of 5 pens = Rs. 85
Cost of 1 pen = \(\frac{85}{5}\) = Rs. 17
∴ Cost of 12 pens = 12 × 17 = Rs. 204
→ Direct proportion: If in two quantities, when one quantity increases, the other also increase or vice-versa then the two quantities are said to be in direct proportion.
Eg: The number of books and their cost are in direct proportion.
As the number of books increases, the cost also increases.
→ Ratios also appear in the form of percentages.
→ The word percent means “per every hundred” or for a hundred. The symbol % is used to denote percentage.
→ To convert a quantity into its equivalent percentage
- express it as a fraction.
- multiply it with 100.
- assign % symbol.
Eg: A man purchased an article for Rs. 80 and sells it for Rs. 100. Find his gain percent.
Solution. Cost price = Rs. 80
Selling price = Rs. 100
gain = Rs. 20
gain as a fraction = \(\frac{20}{80}\)
gain as percent = \(\frac{20}{80}\) × 100 = 25%
![]()
→ When C.P > S.P there incurs loss.
→ When C.P < S.P there is gain.
→ When C.P = S.P neither loss nor gain.
→ Loss = C.P – S.P gain = S.P – C.P
→ Discount is always expressed as some percentage of marked price.
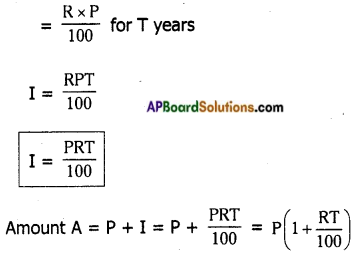
→ In general when P is principle; R% is rate of interest per annum and I is the interest, then
I = R% of P
I = R% of P for T years