SCERT AP 7th Class Maths Solutions Pdf Chapter 11 Area of Plane Figures Ex 11.4 Textbook Exercise Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 11th Lesson Area of Plane Figures Ex 11.4
Question 1.
The radius of a circular-shaped park is 40 m. A path of width 7 m. is played around outside the park. Find the area of the circular path.
Answer:
Given the radius of a park r = 40 m
Area of inner circle = πr2
= \(\frac{22}{7}\) × 40 × 40
= \(\frac{35200}{7}\)
Area of outer circle = πr2
= \(\frac{22}{7}\) × 47 × 47
= \(\frac{48,598}{7}\) = 6942.57 sq.m
Area of the path = Outer circle area – Inner circle area
= 6942.57 – 5028.57
∴ Area of circular path = 1914 sq.m
![]()
Question 2.
Bhuvanesh builds a circular lawn of radius 28 m. in front of his house. A path of 7 m. width is laid around outside the lawn. Find the area of the circular path.
Answer:
Radius of circular lawn r = 28 m
Area of inner circle = πr2
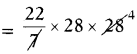
= 2464 sq.m
A path laid outside the lawn.
Width of the path = 7 m.
Radius of the outer circle
= Inner radius + width of path
= 28 + 7 = 35 m
Area of the outer circle = πr2
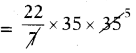
= 3850 sq.m.
Question 3.
A water fountain is in circular shaped whose radius is 12 m. Its inner portion 5 m. arranged for fountain remaining part cemented. Find the area of that cemented part. Find the cost for cementing, if the rate is ₹ 150 per Sq. m.
Answer:
Radius of water fountain r = 12 m
Area of the outer circle = πr2
= \(\frac{22}{7}\) × 12 × 12
= \(\frac{3168}{7}\)
= 452.57 sq.m
Path laid inner side.
So, width of the path = 7 m
Radius of inner circle = Outer radius – width of the path
= 12 – 7 = 5m
Area of the inner circle = πr2
= \(\frac{22}{7}\) × 5 × 5
= 78.57 sq.m.
Width of the path = 5 m
Area of the path = Outer area – Inner area = 452.57 – 78.57.
Area of the circular path = 374 sq.m
Cost of cementing per sq.m = ₹ 150
Cost of cementing per 374 sq.m = 374 × 150
Total cost of cementing = ₹ 56,100
![]()
Question 4.
The radius of circular shaped cricket ground is 55 m. A lobby of 5 m width has been constructed around the ground for spectators. Find the area of lobby. Find the cost of construction of the lobby for seating arrangement, if the rate of construction is ₹ 1500 per Sq. m.
Answer:
Radius of the cricket ground r = 55 m
Area of the cricket ground = πr2
= \(\frac{22}{7}\) × 55 × 55
= \(\frac{66550}{7}\)
= 9507.14 sq.m
Lobby in constructed around the ground.
Radius of the inner circle = Outer radius – width of the path
= 55 – 5 = 50m
Area of the inner circle = πr2
Area of the path = Outer area – Inner area
= 9507.14 – 7857.14 = 1650 sq.m
Cost of constructing seating arrangement per sq.m = ₹ 1500
Cost of seating arrangement per 1650 sq.m = 1650 × 1500 = ₹ 24,75,000