AP State Syllabus AP Board 7th Class Maths Solutions Chapter 13 Area and Perimeter Ex 2 Textbook Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 13th Lesson Area and Perimeter Exercise 2
![]()
Question 1.
Find the area of the each of the following parallelograms.
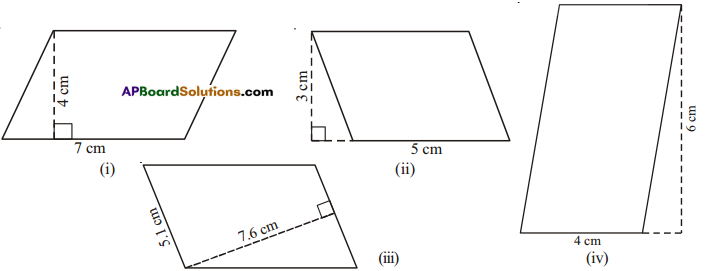
Solution:
| Fig | Base | Height | A = Base x Height |
| (i) | 7 | 4 | 7 x 4 = 28cm2 |
| (ii) | 5 | 3 | 5 x 3 = 15 cm2 |
| (iii) | 5.1 | 7.6 | 5.1 x 7.6 = 38.76 cm2 |
| (iv) | 4 | 6 | 4 x 6 = 24cm2 |
![]()
Question 2.
PQRS is a parallelogram. PM is the height from P to \(\overline{\mathrm{SR}}\) and PN is the height from P to \(\overline{\mathrm{QR}}\). If SR = 12cm and PM = 7.6 cm.
(i) Find the area of the parallelogram PQRS
(ii) Find PN, if QR = 8 cm.
Solution:
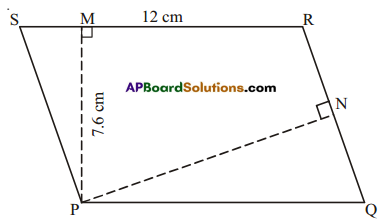
i) Given:SR = 12cm
PM = 7.6cm
∴ Area = base × height
= 12 × 7.6 = 91.2 cm2
ii) Also area = base × height
91.2 = QR × PN
91.2 = 8 × PN
∴ PN = \(\frac{91.2}{8}\) = 11.4cm
Question 3.
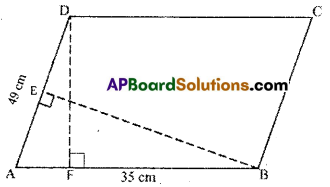
DF and BE are the height on sides AB and AD respectively in parallelogram ABCD. Ifthe area of the parallelogram is 1470 cm2, AB = 35 cm and AD = 49 cm, find the length of BE and DF.
Solution:
Given : AB = 35 cm, AD = 49 cm
area of 🖾ABCD = 1470 cm2
Area of a parallelogram = base × height
AB × DF = area of 🖾ABCD
35 × DF = 1470
DF = \(\frac{1470}{35}\) = 42cm
Also AD × BE = 1470
49 × BE = 1470
∴ BE= \(\frac{1470}{49}\) = 30cm
![]()
Question 4.
The height of a parallelogram is one third of its base. If the area of the parallelogram is 192cm2, find its height and base.
Solution:
Area of the parallelogram = 192 cm2
Area of parallelogram = base × height = 192 cm2 (given)
Let the base of the parallelogram be x.
height = \(\frac{x}{3}\)
Area = base × height = x x \(\frac{x}{3}=\frac{x^{2}}{3}\) = 192
⇒ x2 = 192 × 3 = 576
x = \(\sqrt{576}\) = 24
∴ base = 24 cm
height = \(\frac{x}{3}=\frac{24}{3}\) = 8cm.
![]()
Question 5.
In a parallelogram the base and height are is in the ratio of 5:2. If the area of the parallelogram is 360m2, find its base and height.
Solution:
Let the base of the parallelogram be 5x and height of the parallelogram be 2x.
Area = height x base = 5x × 2x = 10x2 = 360 cm2 (given)
10x2 = 360
x2 = \(\frac{360}{10}\) = 36
x = √36 = 6
base = 5x = 5(6) = 30 cm
height = 2x = 2(6) = 12 cm
Question 6.
A square and a parallelogram have the same area. If a side of the square is 40m and the height of the parallelogram is 20m, find the base of the parallelogram.
Solution:
Given: Side of a square = 40m
Height of a parallelogram = 20m
Area of parallelogram = Area of the square
base × height side × side
base × 20 40 × 40
∴ base = \(\frac{40 \times 40}{20}\) = 80 m.