SCERT AP 7th Class Maths Solutions Pdf Chapter 5 Triangles Ex 5.3 Textbook Exercise Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 5th Lesson Triangles Exercise 5.3
Question 1.
Write the exterior angles of ∆XYZ.
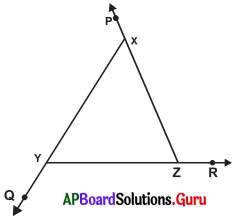
Answer:
Exterior angles of ∆XYZ are ∠PXY, ∠ZYQ and ∠XZR.
Exterior angle of X is ∠PXY. Exterior angle of Y is ∠QYZ.
Exterior angle of Z is ∠XZR.
![]()
Question 2.
Find the exterior angles in each of the following triangles :
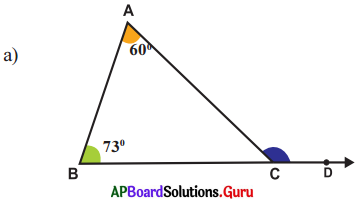
Answer:
From the figure
∠A = 60°, ∠B = 73°
Exterior angle of a triangle is equal to the sum of its opposite interior angles.
Exterior angle at
C = ∠A + ∠B
= 600 + 730
= 133°
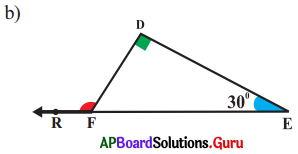
Answer:
From the figure,
∠D = 90°, ∠E = 30°
Exterior angle of a triangle is equal to the sum of its opposite interior angles.
Exterior angle at
F = ∠D + ∠E
= 90° +.30°
= 120°
Question 3.
Find the value of ‘x’ in the following figures.
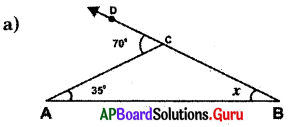
Answer:
From the figure, ∠A = 35°, ∠B = x° and exterior angle at C = 70°
Exterior angle of a triangle is equal to the sum of its opposite interior angles. Exterior anjpNtt
C = ∠A + ∠B = 70°
⇒ 35° + x= 70°
⇒ 35° + x – 35° = 70° – 35°
∴ x = 35°
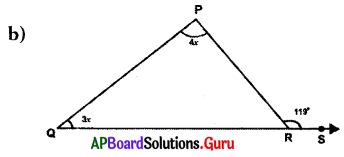
Answer:
From the figure, ∠P = 4x, ∠Q = 3x and exterior angle at R = 119°
Exterior angle of a triangle is equal to the sum of its opposite interior angles.
Exterior angle at R = ∠P + ∠Q = 119°
⇒ 4x + 3x = 119°
⇒ 7x = 119°
⇒ \(\frac{7 x}{7}=\frac{119^{\circ}}{7}\)
∴ x = 17°
![]()
Question 4.
If the exterior angle of a triangle is 110° and it’s interior opposite angles are x° and (x + 10)°, then find the value of ‘x’.
Answer:
Given interior opposite angles are x° and (x + 10)°.
Exterior angle =110° .
Exterior angle of a triangle is equal to the sum of its opposite interior angles.
x + x + 10° = 110°
⇒ 2x + 10°- 10° = 110°- 10°
⇒ 2x = 100°
⇒ \(\frac{2 x}{2}=\frac{100^{\circ}}{2}\)
∴ x = 50°
Question 5.
Find the values of V and ‘y’ in each of the following figures.
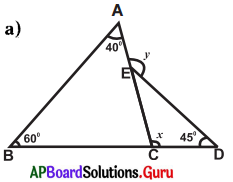
Answer:
From the figure, ∠A = 40°, ∠B = 60°, ∠D = 45°
Exterior angle at C = x°
Exterior angle at E = y°
Exterior angle of a triangle is equal to the sum of its opposite interior angles.
Exterior angle at C = ∠A + ∠B
x = 40° + 60°
∴ x = 100°
Exterior angle at E = ∠C + ∠D
y = x + 45°
y = 100° + 45°
∴ y = 145°
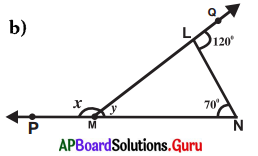
Answer:
From the figure, ∠M = y, ∠N = 70°
Exterior angle at M = x°
Exterior angle at L = 120°
Exterior angle of a triangle is equal to the sum of its opposite interior angles.
Exterior angle at L = ∠M + ∠N = 120°
⇒ y + 70° = 120°
⇒ y + 70 – 70 = 120 – 70
∴ y = 50°
∠QLN + ∠MLN = 180° (linear pair of angles)
120° + ∠MLN = 180°
120° + ∠MLN – 120° = 180°- 120°
∠MLN = 60°
∴ ∠L = 60°
Exterior angle at M = ∠L + ∠N
x = 60° + 70° = 130°
∴ x = 130°
∴ x = 130° and y = 50°