SCERT AP 7th Class Maths Solutions Pdf Chapter 9 Algebraic Expressions InText Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 9th Lesson Algebraic Expressions InText Questions
Check your progress [Page No. 49]
Question 1.
How many number of terms are there in each of the following expressions ?
(i) 5x2 + 3y + 7
Answer:
Given expression is 5x2 + 3y + 7 Number of terms = 3
![]()
(ii) 5x2y + 3
Answer:
Given expression is 5x2y + 3
Number of terms = 2
(iii) 3x2y
Answer:
Given expression is 3x2y
Number of terms = 1
(iv) 5x – 7
Answer:
Given expression is 5x – 7
Number of terms = 2
(v) 7x3 – 2x
Answer:
Given expression is 7x3 – 2x
Number of terms = 2
Question 2.
Write numeric and algebraic terms in ‘ the above expressions.
(i) 5x2 + 3y + 7
Answer:
Given expression is 5x2 + 3y + 7
Numerical terms = 7
Algebraic terms = 5x2, 3y
(ii) 5x2y + 3
Answer:
Given expression is 5x2y + 3
Numerical terms = 3
Algebraic terms = 5x2y
(iii) 3x2y
Answer:
Given expression is 3x2y
Numerical terms = No
Algebraic terms = 3x2y
(iv) 5x – 7
Answer:
Given expression is 5x – 7
Numerical terms = – 7
Algebraic terms = 5x
![]()
(v) 7x3 – 2x
Answer:
Given expression is 7x3 – 2x
Numerical terms = No
Algebraic terms = 7x3, – 2x
Question 3.
Write the terms in the following expressions.
– 3x + 4, 2x – 3y, \(\frac{4}{3}\)a2 + \(\frac{5}{2}\)b,
1.2ab + 5.1b – 3.2a
Answer:
| Expressions | Terms |
| – 3x+4 | – 3x, 4 |
| 2x – 3y | 2x, – 3y |
| \( \frac{4}{3} \)a2 + \( \frac{5}{2} \)b | \( \frac{4}{3} \)a2 + \( \frac{5}{2} \)b |
| 1.2 ab + 5.1 b – 3.2 a | 1.2 ab, 5.1 b, – 3.2a |
Let’s Explore (Page No: 50)
Question 1.
Identify the terms which contain m2 and write the coefficients of m2.
(i) mn2 + m2n
Answer:
Given expression is mn2 + m2n
| m2 term | Coefficeint |
| m2n | n |
(ii) 7m2 – 5m – 3
Answer:
Given expression is 7m2 – 5m – 3
| m2 term | Coefficeint |
| 7m2 | 7 |
![]()
(iii) 11 – 5m2 + n + 8 mn
Answer:
Given expression is 11 – 5m2 + n + 8 mn
| m2 term | Coefficeint |
| – 5m2 | -5 |
Check Your Progress [Page No. 52]
Question 1.
Write like terms from the following :
– xy2, – 4yx, 8x, 2xy2, 7y, – 11x2, – 100x, – 11yx, 20x2y, – 6x2, y, 2xy, 3x
Answer:
Given – xy2, – 4yx, 8x, 2xy2, 7y, – 11x2, – 100x, – 11yx, 20x2y, – 6x2, y, 2xy, 3x
- – xy2, 2xy2 are like terms because they contain same algebraic factor xy2.
- – 4yx, – 11yx, 2xy are like terms because they contain same algebraic factor xy.
- 8x, – 100x, 3x are like terms because they contain same algebraic factor x.
- 7y, y are like terms because they contain same algebraic factor y.
- – 11x2, – 6x2. are like terms because they contain same algebraic factor x2.
Question 2.
Write 3 like terms for
(i) 3x2y
Answer:
Like terms of 3x2y are – 8x2y, \(\frac{5}{3}\) x2y, 2.9 x2y
(ii) – ab2c
Answer:
Like terms of – ab2c are 3ab2c, 5.8 ab2c, \(\frac{-1}{4}\) ab2c.
Let’s Explore [page No: 52]
Question 1.
Jasmin says that 3xyz is a trinomial. Is she right ? Give reason.
Answer:
Given expression 3xyz.
In this expression only one term is there. So, it is a monomial only. But, not trinomial.
So, Jasmin is wrong.
![]()
Question 2.
Give two examples each for Monomial and Binomial algebraic expression.
Answer:
| Type of Expressions | Expressions |
| Monomial | x, b2c, xy2z, ……………….. |
| Binomial | x + 2y, 4b – 3c, x2y – yz, …………… |
Check Your progress [Page No. 54]
Question 1.
Add the following like terms.
(i) 12ab, 9ab, ab
Answer:
Sum of 12ab, 9ab, ab
= 12ab + 9ab + ab
= (12 + 9 + 1) ab
= 22 ab.
(ii) 10x2, – 3x2, 5x2
Answer:
Sum of 10x2, – 3x2, 5x2
= 10x2 + (- 3x2) + 5x2
= 10x2 – 3x2 + 5x2
= (10 – 3 + 5) x2
= 12x2
(iii) – y2, 5y2, 8y2, – 14y2
Answer:
Sum of – y2, 5y2, 8y2, – 14y2
= – y2 + 5y2 + 8y2 + (- 14y2)
= – 1y2 + 5y2 + 8y2 – 14y2
= (- 1 + 5 + 8 – 14) y2
= – 2y2
(iv) 10mn, 6mn, – 2mn, – 7mn
Answer:
Sum of 10mn, 6mn, – 2mn, – 7mn
= 10mn + 6mn + (- 2mn) + (- 7mn)
= 10mn + 6mn – 2mn – 7mn
= (10 + 6 – 2 – 7) mn
= 7mn
![]()
Let’s Think [Page No: 54]
Reshma simplified the expression
4p + 6p + p like this.
4p + 6p + p = 10p. Is she correct ?
Answer:
4p + 6p + p = (4 + 6 + 1)p
= 11p ≠ 10p
So, Reshma simplified is wrong.
Check Your Progress [Page No: 54]
Question 1.
Write the standard form of the following expressions :
(i) – 5l + 2l2 + 4
Answer:
2l2 – 5l + A
(ii) 4b2 + 5 – 3b
Answer:
4b2 – 3b + 5
(iii) z – y – x
Answer:
– x – y + z.
![]()
Check Your Progress [Page No. 56]
Question 1.
Add the following expressions in both Row and Column methods:
(i) x – 2y, 3x + 4y
Answer:

(ii) 4m2 – 7n2 + 5mn, 3n2 + 5m2 – 2mn
Answer:
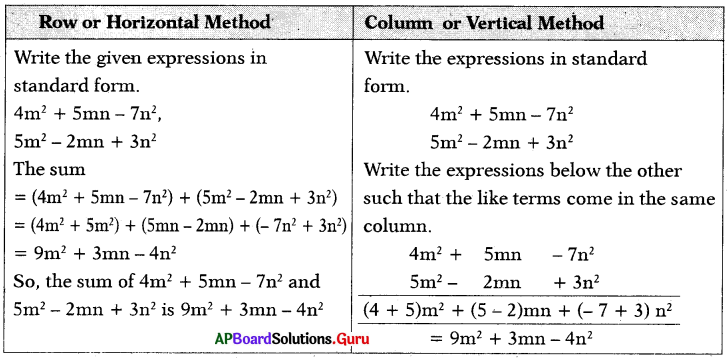
(iii) 3a – 4b, 5c – 7a + 2b
Answer:

![]()
Let’s Explore [Page No. 56]
Think of at least two situations in each of which you need to form two algebraic expressions and add them.
(i) Aditya and Madhu went to a store. Aditya bought 6 books and Madhu bought 2 books. All the books are same cost. How much money did both spend ₹
Answer:
Let the cost of each book ₹a.
Number of books Aditya bought = 6
Cost of 6 books = 6 × a = ₹ 6a
Number of books Madhu bought = 2
Cost of 2 books = 2 × a = ₹ 2a
Money spend on books bought by Aditya and Madhu
= 6a + 2a
= (6 + 2)a
= ₹ 8a
(ii) Sreeja and Sreekari went to icecream parlour. Sreeja bought Vineela icecreams 2 and Sreekari bought Butter Scotch 3. Cost of icecreams are different. How much money they gave to the shop keeper ₹
Answer:
Let the cost of Vineela is ₹x and cost of Butter Scotch is ₹y.
Number of Vineela icecreams Sreeja bought = 2
Cost of 2 iceqreams = 2 × x = ₹ 2x
Number of Butter Scotch icecreams Sreekari bought = 3
Cost of 3 icecreams = 3 × y = ₹ 3y
Money given to shopkeeper = 2x + 3y
= ₹(2x + 3y)
![]()
Check Your Progress [Page No. 57]
Question 1.
Subtract the first term from second term :
(i) 2xy, 7xy
Answer:
7xy – 2xy
= (7 – 2) xy
= 5xy
![]()
(ii) 4a2, 10a2
Answer:
10a2 – 4a2 = (10 – 4)a2 = 6a2
(iii) 15p, 3p
Answer:
3p – 15p = (3 – 15)p = – 12p
(iv) 6m2n, – 20m2n
Answer:
– 20 m2n – 6m2n = (- 20 – 6) m2n
= – 26m2n
(v) a2b2, – a2b2
Answer:
– a2b2 – a2b2 = (- 1 – 1)a2b2 = – 2a2b2
Let’s Explore [Page No. 58]
Add and subtract the following expressions in both Horizontal and Vertical method x – 4y + z, 6z – 2x + 2y
Answer:
Addition

Subtraction:

![]()
Let’s Explore [Page No. 60]
Question 1.
Write an expression whose value is – 15 when x = – 5.
Answer:
Given x = – 5 and value = – 15
Value = – 15 ,
= 3 × – 5 ,
= – 3 × x (∵ x = – 5)
∴ Expression = 3x
Question 2.
Write an expression whose value is 15 when x = 2.
Answer:
Given x = 2 and value = 15
Value = 15
= \(\frac{30}{2}\)
= \(\frac{1}{2}\) × 15 × 2
= \(\frac{1}{2}\) × 15 × x (∵ x = 2)
∴ Expression = \(\frac{15 x}{2}\)
Lets Think [Page No. 60]
While finding the value of an algebraic expression 5x when x = – 2, two stu¬dents solved as follows:

Can you guess who has done it correctly? Justify!
Answer:
Given expression is 5x when x = – 2
5x = 5(- 2) = – 10
Chaitanya is correct.
Here we have to multiply 5 and,- 2.
But Reeta subtracted.
So, Reeta is wrong.
Examples
Question 1.
How many number of terms are there in each of the following expressions ?
(i) a + b
Answer:
a + b ……….. 2 terms
(ii) 3t2
Answer:
3t2 ……….. 1 term
(iii) 9p3 + 10q – 15
Answer:
9p3 + 10q – 15 ……….. 3 terms
(iv) \(\frac{5 \mathrm{~m}}{3 \mathrm{n}}\)
Answer:
\(\frac{5 \mathrm{~m}}{3 \mathrm{n}}\) ……….. 1 term
(v) 4x + 5y – 3z – 1
Answer:
4x + 5y – 3z – 1 ……….. 4 terms
![]()
Question 2.
In the following expressions, write the number of terms and identify numeri¬cal and algebraic expressions in them.
(i) 8p
Answer:
8p = 1 term – Algebraic expression
(ii) 5c + s – 7
Answer:
5c + s – 7 = 3 terms – Algebraic expression
(iii) – 6
Answer:
– 6 = 1 term – Numerical expression
(iv) (2 + 1) – 6
Answer:
(2 + 1) – 6 = 2 terms – Numerical expression
(v) 9t + 15
Answer:
9t + 15 = 2 terms – Algebraic expression
Question 3.
Write the coefficients of
(i) p in 8pq
Answer:
8pq = p(8q)
so, coefficient of p in 8pq is 8q.
(ii) x in \(\frac{x y}{3}\)
Answer:
\(\frac{x y}{3}\) = x\(\left(\frac{\mathrm{y}}{3}\right)\)
so, coefficient of x in \(\frac{x y}{3}\) is \(\left(\frac{\mathrm{y}}{3}\right)\)
(iii) abc in (- abc)
Answer:
(- abc) = – (abc)
so, coefficient of abc is – 1.
Question 4.
Identify like terms among the following and group them:
10ab, 7a, 8b, – a2b2, – 7ba, – 105b, 9b2a2, – 5a2, 90a.
Answer:
(7a, 90a) are like terms because they
contain same algebraic factor ‘a’.
(10ab, – 7ba) are like terms as they have same algebraic factor ’ab’.
(8b, -105b) are like terms because they contain same algebraic factor ‘b’.
(- a2b2, 9b2a2) are like terms because they contain same algebraic factor ‘a2b2‘.
![]()
Question 5.
State with reasons, classify the following expressions into monomials, binomials, trinomials.
a + 4b, 3x2y, px2 + qx + 2, qz2, x2 + 2y, 7xyz, 7x2 + 9y3 – 10z4, 3l2 – m2, x, – abc.
Answer:
| Expressions | Type of the Expression | Reason |
| x, 7xyz, 3x2y, qz2, – abc | Monomial | One term |
| a + 4b, x2 + 2y, 3l2 – m2 | Binomial | Two unlike terms |
| px2 + qx + 2, 7x2 + 9y3 – 10z4 | Trinomial | Three unlike terms |
Question 6.
Find the sum of the following like terms :
(i) 3a, 9a
Answer:
Sum of 3a, 9a = 3a + 9a
= (3 + 9)a = 12a
(ii) 5p2q, 2p2q
Answer:
Sum of 5p2q, 2p2q = 5p2q + 2p2q
= (5 – 2) p2q = 7p2q
(iii) 6m, – 15m, 2m
Answer:
Sum of 6m, – 15m, 2m
= 6m + (- 15m) + 2m
= 6m – 15m + 2m
= (6 – 15 + 2)m = – 7m
Question 7.
Write the perimeter of the given figure.
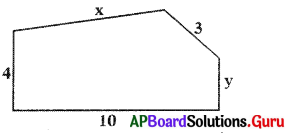
Answer:
The perimeter of the figure
= 10 + 4 + x + 3+ y
= x + y + (10 + 4 + 3)
= x + y + 17
![]()
Question 8.
Simplify:
6a2 + 3ab + 5b2 – 2ab – b2 + 2a2 + 4ab + 2b2 – a2
Answer:
6a2 + 3ab + 5b2 – 2ab – b2 + 2a2 + 4ab + 2b2 – a2
= (6a2 + 2a2 – a2) + (3ab – 2ab + 4ab) + (5b2 – b2 + 2b2)
= [(6 + 2 – 1) a2] + [(3 – 2 + 4)ab] + [(5 – 1 + 2)b2]
= 7a2 + 5ab + 6b2
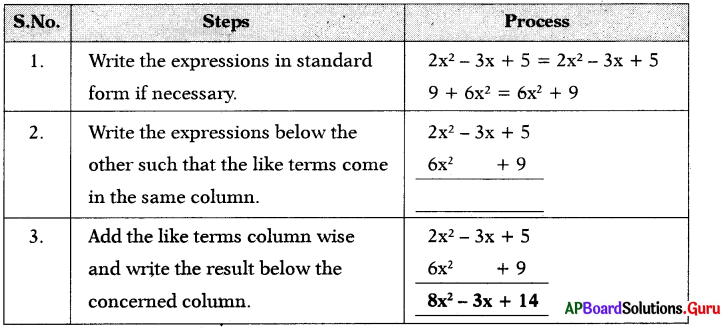
Question 9.
Add 2x2 – 3x + 5 and 9 + 6x2 in vertical method.

Answer:
Question 10.
Find the additive inverse of the follow-ing expressions:
(i) 35
Answer:
Additive inverse of 35 = – 35
![]()
(ii) – 5a
Answer:
Additive inverse of – 5a = – (-5a) = 5a
(iii) 3p – 7
Answer:
Additive inverse of 3p – 7 = – (3p – 7) = – 3p + 7
(iv) 6x2 – 4x + 5
Answer:
Additive inverse of 6x2 – 4x + 5
= (6x2 – 4x + 5) = – 6x2 + 4x – 5
Question 11.
Subtract 2p2 – 3 from 9p2 – 8.
Answer:
9p2 – 8 – (2p2 – 3) = 9p2 – 8 – 2p2 + 3
= (9 – 2) p2 – 8 + 3
= 7p2 – 5
Question 12.
Subtract 3a + 4b – 2c from 6a – 2b + 3c in row method.
Answer:
Let A = 6a – 2b + 3c, B = 3a + 4b – 2c
Subtracting 3a + 4b – 2c from 6a – 2b + 3c is equal to adding additive inverse of 3a + 4b – 2c to 6a – 2b + 3c
i.e., A – B = A + (-B)
additive inverse of (3a + 4b – 2c) = – (3a + 4b – 2c) = – 3a – 4b + 2c
A – B = A + (-B)
= 6a – 2b + 3c + (- 3a – 4b + 2c)
= 6a – 2b + 3c – 3a – 4b +2c = (6 – 3)a – (2 + 4)b + (3 + 2)c
Thus, the required answer = 3a – 6b + 5c
Question 13.
Subtract 3m3 + 4 from 6m3 + 4m2 + 7m – 3 in stepwise method.
Answer:
Let us solve this in stepwise.
Step 1: 6m3 + 4m2 + 7m – 3 – (3m3 + 4)
Step 2: 6m3 + 4m2 + 7m – 3 – 3m3 – 4
Step 3: 6m3 – 3m3 + 4m2 + 7m – 3 – 4 (rearranging like terms)
Step 4: (6 – 3)m3 + 4m2 + 7m – 7 (distributive law)
Thus, the required answer = 3m3 + 4m2 + 7m – 7
![]()
Question 14.
Subtract 4m2 – 7n2 + 5mn from 3n2 + 5m2 – 2mn.
(For easy understanding, same colours are taken to like terms)
Answer:
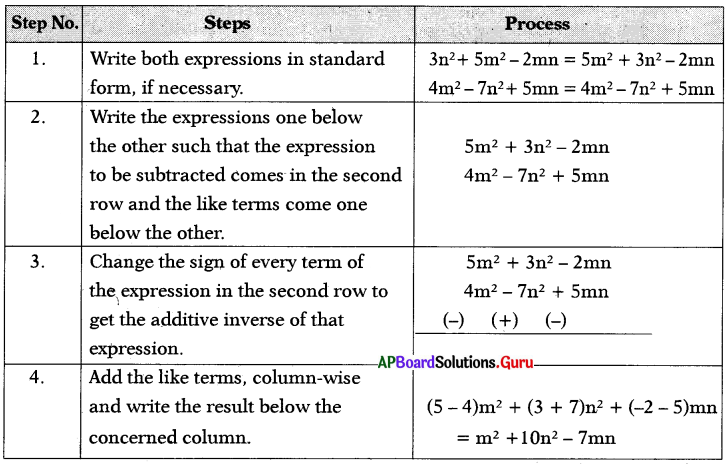
Question 15.
Find the value of the following expressions, when x = 3.
(i) x + 6
Answer:
When x = 3, the value of x + 6
(substituting 3 in the place of x) is
(3) + 6 = 9
(ii) 8x – 1
Answer:
When x = 3,
the value of 8x – 1 = 8(3) – 1
= 24 – 1 = 23
(iii) 14 – 5x
Answer:
When x = 3,
the value of 14 – 5x = 14 – 5(3)
= 14 – 15 = – 1
![]()
Practice Questions [Page No: 65]
Question 1.
In a certain code BOARD: CNBQE, how ANGLE will be written in that code?
(a) BMHKF
(b) CNIJE
(c) BLGIF
(d) CMIKF
Answer:
(a) BMHKF
Explaination:
Each letter in a word is shifted to 1 position is alphabetical order and went 1 position is backward like this.
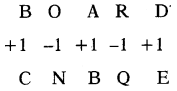
ANGLE = BMHKF
Question 2.
In a certain code, MOBILE: 56, how PHONE will be written in that code?
(a) 52
(b) 54
(c) 56
(d) 58
Answer:
(d) 58
Explaination:
Taking sum of positions of letters in for ward direction.
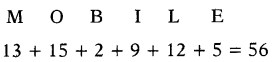
So, PHONE = 16 + 8 + 15 + 14 + 5 = 58
Question 3.
If BEAN: ABNE, then NEWS ?
(a) WSNE
(b) WSEN
(c) WNSE
(d) WNES
Answer:
(c) WNSE
Explaination:
Follow the same to decode the given word.

![]()
Question 4.
If ROSE : 6821, CHAIR : 73456, PREACH : 961473, then SEARCH ?
(a) 241673
(b) 214673
(c) 216473
(d) 216743
Answer:
(b) 214673
Explaination:
By comparing each letter with the symbol, by writing one below the other.

Question 5.
If COMPUTER: RFUVQNPC, then MEDICINE?
(a) EDJOJMEF
(b) EOJDJEFM
(c) EOJJDFEM
(d) EDJJOFME
Answer:
(b) EOJDJEFM
Explaination:
In the coded form the first & last letters have been interchanged while the rem¬aining letters are coded by taking their immediate next letters in the reverse order.
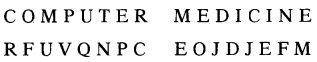
Question 6.
If LAKE = 7@$5, WALK = %@7$, then WAKE = ?
(a) @%75
(b) %@$5
(c) %5@7
(d) %@57
Answer:
(b) %@$5
Explaination:
By comparing each letter with symbol, by writing One below the other.
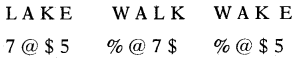
![]()
Question 7.
If MANY = OCPA, then LOOK = ?
(a) NQQM
(b) MQQN
(c) QMQN
(d) QNQM
Answer:
(a) NQQM
Explaination:
Each letter in a word is shifted to 2 position forward in alphabetical order.
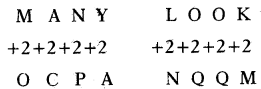
∴ LOOK = NQQM
Question 8.
If SOME = PUB, then BODY ?‘
(a) LABY
(b)YBAL
(c) YLAV
(d) ABLY
Answer:
(c) YLAV
Explaination:
Bach letter in a word is shifted to 3 position backward in alphabetical order.
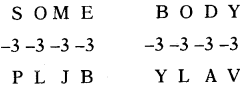
So, BODY = YLAV
Question 9.
If ARC = CVI, then RAY?
(a) TEU
(b) TEE
(c) TED
(d) TEF
Answer:
(b) TEE
Explaination:
Each letter in a word is forwarded alphabetical order as follows.

So, RAY = TEE
![]()
Question 10.
If MEAN = KGYI, then MODE = ?
(a) QBGK
(b) KBQC
(c) KGBQ
(d) kQBG
Answer:
(d) kQBG
Explaination:
Each letter in the word is shifted to 2 position backward and 2 position forward as following.
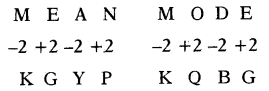
So, MODE = KQBG
Question 11.
If FIND = DNIF, then DONE ?
(a) ENOD
(b) ENDO
(c) NEOD
(d) ONED
Answer:
(a) ENOD
Explaination:
By reversing the word from left to right.
So, DONE = ENOD .
Question 12.
If BASE = SBEA, then AREA = ?
(a) AARE
(b) EAAR
(c) EARA
(d) REAA
Answer:
(b) EAAR
Explaination:
Follow the same to decode the given word.
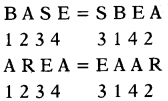
![]()
Question 13.
If LESS = 55, then MORE = ?
(a)54
(b)50
(c) 51
(d) 52
Answer:
(c) 51
Explaination:
Taking sum of positions of letters in forward direction.
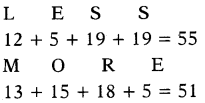
Question 14.
If BACK = 17, then CELL =?
(a) 33
(b) 30
(c) 31
(d) 32
Answer:
(d) 32
Explaination:
Taking sum of positions of letters in for ward direction.
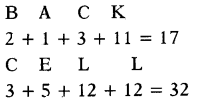
3 + 5 + 12 + 12 = 32
Question 15.
If BIG = 63, then SMALL =?
(a) 76
(b) 78
(c) 74
(d) 72
Answer:
(b) 78
Explaination:
Taking sum of positions of letters in reverse direction.
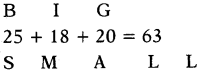
8 + 14 + 26 + 15 + 15 = 78