AP Board 8th Class Maths Solutions Chapter 11 Algebraic Expressions InText Questions

AP State Syllabus 8th Class Maths Solutions 11th Lesson Algebraic Expressions InText Questions

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 11 Algebraic Expressions InText Questions and Answers.

8th Class Maths 11th Lesson Algebraic Expressions InText Questions and Answers

Do this

Question 1.
Find the number of terms in following algebraic expressions.
5xy², 5xy³ – 9x, 3xy + 4y – 8, 9x² + 2x + pq + q.    [Page No. 248]
Answer:

Question 2.
Take different values for x and find values of 3x + 5.     [Page No. 248]
Answer:
If x = 1 then 3x + 5 = 3(1) + 5 = 3 + 5 = 8
If x = 2 then 3x + 5 = 3(2) + 5 = 6 + 5 = 11
If x = 3 then 3x + 5 = 3(3) + 5 = 9 + 5 = 14

Question 3.
Find the like terms in the following: ax²y, 2x, 5y², -9x², -6x, 7xy, 18y².    [Pg. No. 249]
Answer:
Like terms are (2x, – 6x) (5y², 18y²).

Question 4.
Write 3 like terms for 5pq².     [Pg. No. 249]
Answer:
Like terms of 5pq² are – 3pq², pq², \(\frac{\mathrm{pq}^{2}}{2}\)etc.,

Question 5.
If A = 2y² + 3x – x², B = 3x² – y² and C = 5x² – 3xy then find          [Pg. No. 250]
(i) A + B (ii) A – B (iii) B + C (iv) B – C (v) A + B + C (vi) A + B – C
Answer:
A = 2y² + 3x – x², B = 3x² – y², C = 5x² – 3xy
i) A + B = (2y² + 3x – x²) + (3x² – y²)
= (2y² – y²) + 3x + (3x² – x²)
∴ A + B = y² + 3x + 2x² = 2x² + 3x + y²

ii) A – B = (2y² + 3x – x²) – (3x² – y²)
= 2y² + 3x – x² – 3x² + y²
∴ A – B = 3y² + 3x – 4x²

iii) B + C = (3x² – y²) + (5x² – 3xy)
= 3x² + 5x² – y² – 3xy
∴ B + C = 8x² – y² – 3xy

iv) B – C = (3x² – y²) – (5x² – 3xy)
= 3x² – y² – 5x² + 3xy
∴ B – C = – 2x² – y² + 3xy

v) A + B + C = A + (B + C)
= (2y² + 3x – x²) + (8x² – y² – 3xy)
= (8x² – x²) + (2y² – y²) + 3x – 3xy
∴ A + B + C = 7x² + y² + 3x – 3xy

vi) A + B – C = A + (B – C)
= (2y² + 3x – x²) + (-2x² – y² + 3xy)
= (2y² – y²) + (-x² – 2x²) + 3x + 3xy :
∴ A + B – C = y² – 3x² + 3x + 3xy

Question 6.
Complete the table:       [Page No. 253]

Answer:

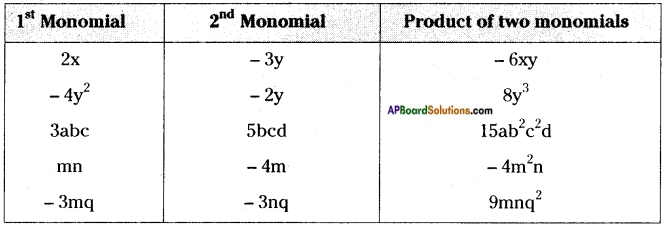
Question 7.
Check whether you always get a monomial when two monomials are multiplied.        [Page No. 253]
Answer:
Yes, the product of two monomials is always a monomial.
Ex: 2xy × 5y = 10xy is a monomial.

Question 8.
Product of two monomials is a monomial? Check.     [Pg. No. 253]
Answer:
Yes, the product of two monomials is a monomial.
∵ 2x × y = 2xy

Question 9.
Find the product: (i) 3x(4ax + 8by) (ii) 4a²b(a – 3b) (iii) (p + Sq²) pq (iv) (m³ + n³) 5mn²       [Pg. No. 255]
Answer:
i) 3x (4ax + 8by) = 3x × 4ax + 3x × 8by
= 12ax² + 24bxy

ii) 4a²b (a – 3b) = 4a²b × a – 4a²b × 3b
= 4a³b – 12a²b²

iii) (p + 3q²) pq = p × pq + 3q² × pq
= p²q + 3pq³

iv) (m³ + n³) 5mn² = m³ × 5mn² + n³ × 5mn²
= 5m⁴n² + 5mn⁵

Question 10.
Find the number of maximum terms in the product of a monomial and a binomial?       [Pg. No. 255]
Answer:
The no.of terms in the product of a monomial and a binomial are two (2).

Question 11.
Find the product:       [Pg. No. 257]
(i) (a – b) (2a + 4b)
(ii) (3x + 2y) (3y – 4x)
(iii) (2m – l)(2l – m)
(iv) (k + 3m)(3m – k)
Answer:
i) (a – b) (2a + 4b) = a(2a + 4b) – b(2a + 4b)
= (a × 2a + a × 4b) – (b × 2a + b × 4b)
= 2a² + 4ab – (2ab + 4b²)
= 2a² + 4ab – 2ab – 4b²
= 2a² + 2ab – 4b²

ii) (3x + 2y) (3y – 4x) = 3x(3y – 4x) + 2y(3y – 4x)
= 9xy – 12x² + 6y² – 8xy
= xy – 12x² + 6y²

iii) (2m – l) (2l – m) = 2m(2l – m) – l(2l – m)
= 2m × 2l – 2m × m – l × 2l + l × m
= 4lm – 2m² – 2l² + lm
= 5lm – 2m² – 2l²

iv) (k + 3m) (3m – k) = k(3m – k) + 3m(3m – k)
= k × 3m – k × k + 3m × 3m – 3m × k
= 3km – k² + 9m² – 3km
= 9m² – k²

Question 12.
How many number of terms will be there in the product df two binomials?        [Page No. 257]
Answer:
No. of terms in the product of two binomials are 4.
Ex: (a + b) (c + d) = ac + ad + be + bd

Question 13.
Verify the following are identities by taking a, b, c as positive integers.    [Pg. No. 260]
(i) (a – b)² = a² – 2ab + b²
(ii) (a + b) (a – b) = a² – b²
(iii) (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca
Answer:
i) (a – b)² = a² – 2ab + b²
a = 3, b = 1
⇒ (3 – 1)² = (3)² – 2 × 3 × 1 + 1²
⇒ (2)² = 9 – 6 + 1
⇒ 4 = 4
∴ (i) is an identity,

ii) (a + b) (a – b) = a² – b²
a = 2, b = 1
⇒ (2 + 1) (2 – 1) = (2)² – (1)²
⇒ 3 × 1 = 4 – 1
⇒ 3 = 3
∴ (ii) is an identity.

iii) (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca
a = 1, b = 2, c = 0
⇒ (1 + 2 + 0)² = 1² + 2² + 0² + 2 × 1 × 2 + 2 × 2 × 0 + 2 × 0 × 1
⇒ (3)² = 1 + 4 + 0 + 4 + 0 + 0
⇒ 9 = 1 + 4 + 4
⇒ 9 = 9
∴ (iii) is an identity.

Question 14.
Now take x = 2, a = 1 and b = 3, verify the identity (x + a) (x + b) s x + (a + b)x + ab.        [Pg. No. 260]
i) What do you observe? Is LHS = RHS?
ii) Take different values for x, a and b for verification of the above identity.
iii) Is it always LHS = RHS for all values of a and b?
Answer:
i) (x + a) (x + b) = x² + (a + b)x + ab
x = 2, a = 1, b = 3 then
⇒ (2 + 1) (2 + 3) = 2² + (1 + 3)² + 1 × 3
⇒ 3 × 5 = 4 + 4x² + 3
⇒ 15 = 4 + 8 + 3 ⇒ 15 = 15
∴ LHS = RHS

ii) x = 0, a = 1, b = 2 then
⇒ (0 + 1) (0 + 2) = 0² + (1 + 2) 0 + 1 × 2
⇒ 1 × 2 = 0 + 0 + 2
⇒ 2 = 2
∴ LHS = RHS for different values of x, a, b.

iii) LHS = RHS for all the values of a, b.

Question 15.
Consider (x + p) (x + q) = x + (p + q)x + pq.
(i) Put q instead of ‘p’ what do you observe?
(ii) Put p instead of ‘q’ what do you observe?
(iii) What identities you observed in your results?            [Pg. No. 261]
Answer:
i) (x + p) (x + q) = x² + (p + q)x + pq …… (1)
Substitute q instead of p in (1).
⇒ (x + q) (x + q) = x² + (q + q)x + q × q
⇒ (x + q)² = x² + 2qx + q²

ii) Substitute ‘p’ instead of q in (1).
⇒ (x + p) (x + p) = x² + (p + p)x + p × p
⇒ (x + p) = x² + 2px + p²

iii) ∴ I observe the following identities.
(x + q)² = x² + 2qx + q²
(x + p)² = x² + 2px + p²

Question 16.
Find: (i) (5m + 7n)²
(ii) (6kl + 7mn)²
(iii) (5a² + 6b²)²
(iv) 302²
(v) 807²
(vi) 704²
(vii) Verify the identity: (a – b)² = a² – 2ab + b², where a = 3m and b = 5n.         [Pg. No. 261]
Answer:
i) (5m + 7n)² is in the form of (a + b)².
(a + b)² = a² + 2ab + b² [a = 5m, b = 7n]
(5m + 7n)² = (5m)² + 2 × 5m × 7n + (7n)²
= (5m × 5m) + 70 mn + 7n × 7n
= 25m² + 70mn + 49n²

ii) (6kl + 7mn)²
We know that (a + b)² = a² + 2ab + b²
∴ (6kl + 7mn)² = (6kl)² + 2 × 6kl × 7mn + (7mn)²
= 36 k²l² + 84 klmn + 49 m²n²

iii) (5a² + 6b²)²
a = 5a², b = 6b²
(5a² + 6b²)² = (5a²)² + 2 × 5a² × 6b² + (6b²)²
= (5a² × 5a²) + 60a²b² + (6b² × 6b²)
= 25a⁴ + 60a²b² + 36b⁴

iv) (302)² = (300 + 2)²
a = 300, b = 2
∴ (300 + 2)² = (300)² + 2 × 300 × 2 + (2)²
= (300 × 300) + 1200 + (2 × 2)
= 90,000 + 1200 + 4
= 91,204

v) (807)² = (800 + 7)²
a = 800, b = 7
∴ (800 + 7)² = (800)² + 2 × 800 × 7 + (7)²
= (800 × 800) + 11,200 + (7 × 7)
= 6,40,000 + 11,200 + 49
= 6,51,249

vi) (704)² = (700 + 4)²
a = 700, b = 4
∴ (700 + 4)² = (700)² + 2 × 700 × 4 + 4²
= (700 × 700) + 5600 +(4 × 4)
= 4,90,000 + 5600 + 16
= 4,95,616

vii) (a – b)² = a² – 2ab + b² …… (1)
Substitute a = 3m, b = 5n in (1).
LHS = (3m – 5n)² = (3m)² – 2 × 3m × 5n + (5n)²
= 9m² – 30mn + 25n²
RHS = (3m)² – 2 × 3m × 5n + (5n)²
= 9m² – 30mn + 25n²
∴ LHS = RHS

Question 17.
Find:
(i)(9m – 2n)²
(ii) (6pq – 7rs)²
(iii) (5x² – 6y²)²
(iv) 292²
(v) 897²
(vi) 794²        [Pg. No. 262]
Answer:
i) (9m – 2n)² is in the form of (a – b)².
(a – b)² = a² – 2ab + b²
(9m – 2n)² = (9m)² – 2 × 9m × 2n + (2n)²
= (9m × 9m) – 36mn + (2n × 2n)
= 81m² – 36mn + 4n²

ii) (6pq – 7rs)²
a = 6pq, b = 7rs
(6pq – 7rs)² = (6pq)² – 2 × 6pq × 7rs + (7rs)²
= (6pq × 6pq) – 84pqrs + (7rs × 7rs)
= 36p²q² – 84pqrs + 49r²s²

iii) (5x² – 6y²)² = (5x²)² – 2 × 5x² × 6y² + (6y²)²
= (5x² × 5x²) – 60x²y² + (6y² × 6y²)
= 25x⁴ – 60x²y² + 36y⁴

iv) (292)² = (300 – 8)²
a = 300, b = 8
∴ (300 – 8)² = (300)² – 2 × 300 × 8 + (8)² = (300 × 300) – 4800 + (8 × 8)
= 90,000 – 4800 + 64
= 90,064 – 4800
= 85,264

v) (897)² = (900 – 3)²
= (900)² – 2 × 900 × 3 + (3)²
= 8,10,000 – 5400 + 9
= 8,10,009 – 5400
= 8,04,609

vi) (794)² = (800 – 6)²
= (800)² – 2 × 800 × 6 + (6)²
= 6,40,000 – 9600 + 36
= 6,40,036 – 9600
= 6,30,436

Question 18.
Find:
(i) (6m + 7n) (6m – 7n)
(ii) (5a + 10b) (5a – 10b)
(iii) (3x² + 4y²) (3x² – 4y²)
(iv) 106 × 94
(v) 592 × 608
(vi) 92² – 8²
(vi) 984² – 16²      [Pg. No. 262]
Answer:
i) (6m + 7n) (6m -,7n) is in the form of (a + b) (a – b). (a + b) (a – b) = a² – b²,
here a = 6m, b = 7n
(6m + 7n) (6m – 7n) = (6m)² – (7n)²
= 6m × 6m – 7n × 7n
= 36m² – 49n²

ii) (5a + 10b) (5a – 10b) = (5a)² – (10b)² [∵ (a + b) (a – b) = a² – b²]
= 5a × 5a – 10b × 10b
= 25a² – 100b²

iii) (3x² + 4y²) (3x² – 4y²)
= (3x²)² – (4y²)²
= 3x² × 3x² – 4y² × 4y²
= 9x⁴-16y⁴ [∵ (a + b) (a – b) = a² – b²]

iv) 106 × 94 = (100 + 6) (100 – 6)
= 100² – 6² = 100 × 100 – 6 × 6 [∵ (a + b) (a- b) = a²– b²]
= 10,000 – 36
= 9,964

v) 592 × 608 = (600 – 8) (600 + 8)
= (600)² – (8)²
= 600 × 600 – 8 × 8
= 3,60,000 – 64
= 3,59,936

vi) 92² – 8² is in the form of a² – b² = (a + b) (a – b).
92² – 8² = (92 + 8)(92 – 8)
= 100 × 84
= 8400

vii) 9842 – 162 = (984 + 16) (984 – 16)
= (1000) (968) [∵ (a + b)(a – b) = a² – b²]
= 9,68,000

Try These

Question 1.
Write an algebraic expression using speed and time; simple interest to be paid, using principal and the rate of simple interest.    [Pg. No. 251]
Answer:
Distance = speed × time
d = s × t

Question 2.
Can you think of two more such situations, where we can express in algebraic expressions?     [Pg. No. 251]
Answer:
Algebraic expressions are used in the following situations:
i) Area of a triangle = \(\frac{1}{2}\) × base × height = \(\frac{1}{2}\) bh
ii) Perimeter of a rectangle = 2(length + breadth) = 2(l + b)

Think, Discuss and Write

Question 1.
Sheela says the sum of 2pq and 4pq is 8p²q² is she right? Give your explanation.      [Pg. No. 249]
Answer:
The sum of 2pq and 4pq = 2pq + 4pq = 6pq
According to Sheela’s solution it is 8p²q².
6pq ≠ 8p²q²
Sheela’s solution is wrong.

Question 2.
Rehman added 4x and 7y and got 1 lxy. Do you agree with Rehman?     [Pg. No. 249]
Answer:
The sum of 4x and 7y
= (4x) + (7y)
= 4x + 7y ≠ 11xy
I do not agree with Rehman’s solution.