AP Board 8th Class Maths Solutions Chapter 11 Algebraic Expressions Ex 11.2

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 11 Algebraic Expressions Ex 11.2 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 11th Lesson Algebraic Expressions Exercise 11.2

Question 1.
Complete the table:

Solution:

Question 2.
Simplify: 4y(3y + 4)
Solution:
4y(3y + 4) = 4y × 3y + 4y × 4
= 12y² + 6y

Question 3.
Simplify x(2x² – 7x + 3) and find the values of it for (i) x = 1 and (ii) x = 0
Solution:
x(2x² – 7x + 3)
= x × 2x² – x × 7x + x × 3
= 2x³ – 7x² + 3x
= 3 × 3 – 1 × 3 – 3 × 1 + 1 × 1
=9 – 3 – 3 + 1 = 4
∴(a – b)² = 4sq.units
[∵ (3 – 1)² = 2² = 4]

(ii)

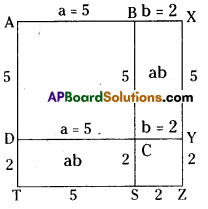
∴ (a – b)² = a² – 2ab + b²
Area of ABCD + Area of CYZS
= a² – 2ab + b²
area of ABCD – area of BXYC – area of DCST + area of CYZS
= 5 × 5 – 2 × 5 – 2 × 5 + 2 × 2
= 25 – 10 – 10 + 4
= 9 sq.units
[∵ (5 – 2)² = (3)² = 9]

Question 4.
Add the product: a(a – b), b(b – c), c(c – a)
Solution:
a(a – b) + b(b – c) + c(c – a)
=a × a – a × b + b × b – b × c + c × c – c × a
=a² – ab + b² – bc + c² – ca
=a² + b² + c² – ab – bc – ca

Question 5.
Add the product: x(x + y – r), y(x – y+r), z(x – y – z)
Solution:
x(x + y – r) +y(x – y + r) + z(x – y – z)
= x² + xy – xr + xy – y² + yr + zx – yz – z²
= x² – y² – z² + 2xy – xr + yr + zx – yz

Question 6.
Subtract the product of 2x(5x – y) from product of 3x(x+2y)
Solution:
3x(x + 2y) – 2x(5x – y)
=(3x × x + 3x × 2y)-(2x × 5x – 2x × y)
= 3x² + 6xy – (10x² – 2xy)
= 3x² + 6xy- 10x² + 2xy
= 8xy – 7x²

Question 7.
Subtract 3k(5k – l + 3rn) from 6k(2k + 3l – 2rn)
Solution:
6k(2k + 3l – 2m) – 3k(5k – l + 3m)
= 12k²+ 18kl – 12km – 15k² + 3kl – 9km
= -3k² + 21kl – 21km

Question 8.
Simplify: a²(a – b + c) + b²(a + b – c) – c²(a – b – c)
Solution:
a²(a – b + c) + b²(a + b – c) – c²(a – b – c)
= a³ – a²b + a²c + ab² + b³ – b²c – ac² + bc² + c³
= a³ + b³ + c³ – a²b + a²c + ab² – b²c – ac² – bc²