AP Board 8th Class Maths Solutions Chapter 15 సంఖ్యలతో ఆడుకుందాం Ex 15.6

AP SCERT 8th Class Maths Textbook Solutions Chapter 15 సంఖ్యలతో ఆడుకుందాం Ex 15.6 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 15th Lesson సంఖ్యలతో ఆడుకుందాం Exercise 15.6

ప్రశ్న 1.
1 నుండి 100 వరకు గల సంఖ్యలలో 5చే భాగింపబడు సంఖ్యల మొత్తం కనుగొనండి.
సాధన.
1 నుండి 100 వరకు గల సంఖ్యలలో 5చే భాగింపబడు సంఖ్యలు 5, 10, 15, ……… 100
ఆ సంఖ్యల మొత్తం = 5 + 10 + 15 + ……… + 100
= 5 (1 + 2 + ………. + 20)
మొదటి ‘n సహజ సంఖ్యల మొత్తం = \(\frac{n(n+1)}{2}\)
= \(\frac{5 \times 20(20+1)}{2}\) = 5 × 10 × 21 = 1050 (∵ n = 20)

ప్రశ్న 2.
11 నుండి 50 వరకు గల సంఖ్యలలో 2చే భాగింపబడు సంఖ్యల మొత్తం కనుగొనండి.
సాధన.
11 నుండి 50 వరకు గల సంఖ్యలలో 2చే భాగింపబడు సంఖ్యలు = 12, 14, 16, …………., 48, 50
ఆ సంఖ్యల మొత్తం = 12 + 14 + 16 + …… + 48 + 50.
= (2 + 4 + …… + 50) – (2 + 4 + …… + 10)
= 2(1 + 2 + …… + 25) – 2(1 + 2 + …… + 5)
= 2[25 × \(\frac{(25+1)}{2}-\frac{5 \times(5+1)}{2}\)
= 2[25 × 13 – 5 × 3]
= 2[325 – 15] = 2 × 310 = 620

ప్రశ్న 3.
1 నుండి 50 వరకు గల సంఖ్యలలో 2 మరియు 3చే భాగింపఐదు సంఖ్యల మొత్తం కనుక్కోంది.
సాధన.
1 నుండి 50 వరకు గల సంఖ్యలలో 2. మరియు 3లచే భాగింపబడు సంఖ్యలు అనగా ‘6’చే భాగింపబడు సంఖ్యలను తీసుకొనగా ఆ సంఖ్యల మొత్తం
= 6 + 12 + …… + 48
= 6(1 + 2 + ….. + 8)
= \(\frac {6(8)(8+1)}{2}\)
= 6 × 4 × 9 = 216

ప్రశ్న 4.
(n³ – n), 3చే భాగింపబడును. వివరించండి.
(లేదా)
“n” సహజసంఖ్య అయిన (n³ – n) ఎల్లప్పుడూ 3చే భాగించబడునా ? వివరించుము.
సాధన.
1వ పద్ధతి:

∴ n యొక్క అన్ని విలువలకు (n³ – n), 3 చే భాగింపబడుతుంది.

2వ పద్ధతి:
n² – n = n(n² – 1) = n(n² – 1²) = (n – 1)
n(n + 1) లు మూడు వరుస సంఖ్యల లబ్ధం కావున ఇది 3చే నిశ్శేషంగా భాగింపబడుతుంది.
∴ (n³ – n), 3 చే భాగింపబడుతుంది.

ప్రశ్న 5.
n వరుస సంఖ్యల మొత్తం (n భసిసంఖ్య) n చే భాగింపబడును. కారణం వివరించండి.
సాధన.
n వరుస బేసిసంఖ్యల మొత్తం = \(\frac{(2 n-1)(2 n)}{2}\) = n(2n – 1)
ఇది n యొక్క గుణిజం కావున ‘n’ చే నిశ్శేషంగా భాగింపబడుతుంది.

ప్రశ్న 6.
1¹¹ + 2¹¹ + 3¹¹ + 4¹¹, 5చే భాగింపబడుతుందా? వివరించండి.
సాధన.
1¹¹ + 2¹¹ + 3¹¹ + 4¹¹ సంఖ్యలో ఒకట్ల స్థానంలోని అంకెల మొత్తం
= 1 + 8 + 7 + 4 = 20 = 20 → \(\frac {0}{5}\) (R = 0)
∴ (1¹¹ + 2¹¹ + 3¹¹ + 4¹¹), 5చే భాగింపబడుతుంది.

ప్రశ్న 7.

పై బొమ్మలో ఎన్ని దీర్ఘచతురస్రాలున్నాయి ?
సాధన.

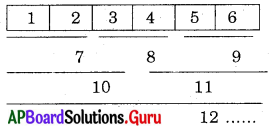
∴ పై చిత్రంలోని దీర్ఘచతురస్రాల సంఖ్య
= 1 + 2 + 3 + 4 + 5 + 6 = 21

ప్రశ్న 8.
రాహుల్ తండ్రి, రాహుల్ పుట్టినరోజునాడు ప్రతి సంవత్సరము కొంత సొమ్ము బ్యాంకులో జమ చేయుచున్నాడు. అతని మొదటి పుట్టినరోజున రూ. 100, రెండవ పుట్టినరోజున రూ. 300, మూడవ పుట్టినరోజున రూ. 600, 4వ పుట్టిన రోజున రూ. 1000, అయితే అతడి 15వ పుట్టినరోజున ఎంత జమచేసి ఉంటాడు?
సాధన.

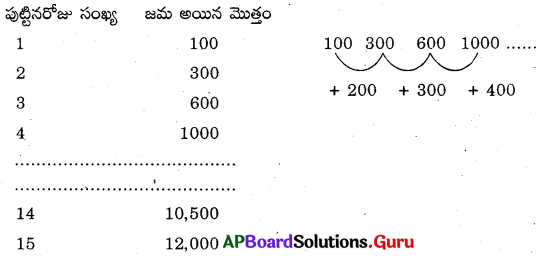
రాహుల్ తండ్రి ప్రతి పుట్టినరోజుకు 200, 300, 100, ……. చొప్పున పెంచుకుంటూ పోతే 14న పుట్టినరోజుకు అతను రూ. 10,500 జము, చేస్తే 16వ పుట్టినరోజుకు జను చేయు మొత్తం = 10,500 + 1,500 = రూ. 12,000

ప్రశ్న 9.
1 నుండి 100 వరకు గల సంఖ్యలలో 2 లేక 5 చే భాగింపబడు సంఖ్యల మొత్తం కనుగొనుము.
సాధన.
1 నుండి 100 వరకు గల సంఖ్యలలో 2చే భాగింపబడే సంఖ్యల మొత్తం
= 2 + 4 + …… + 100 = 2(1 + 2 + ……. + 50)
= \(\frac{2(50)(50+1)}{2}\) = 50 × 51 = 2550
1 నుండి 100 వరకు గల సంఖ్యలలో 5 చే భాగింపబడే సంఖ్యల మొత్తం
= 5 + 10 + 15 + ……. + 100 = 5(1 + 2 + ……. + 20)
= \(\frac{5(20)(20+1)}{2}\)
= 50 × 21 = 1050
∴ 2 మరియు 5చే భాగింపబడే సంఖ్యల మొత్తం = 2550 + 1050 = 3600
దీని నుండి 2 మరియు 5చే (రెండింటిచే) భాగింపబడే సంఖ్యల మొత్తం తీసివేయవలెను.
2 మరియు 5చే భాగింపబడే సంఖ్యల మొత్తం = 10 + 20 + …….. + 100
= 10(1 + 2 + ……. + 10)
= \(\frac{10(10)(10+1)}{2}\)
= 10 × 5 × 11 = 550
∴ కావలసిన సంఖ్యల మొత్తం = 3600 – 550 = 3050

ప్రశ్న 10.
11 నుండి 1000 వరకు గల సంఖ్యలలో 3చే భాగింపబడు సంఖ్యల మొత్తం కనుక్కోండి.
సాధన.
11 నుంది. 1000 వరకు గల సంఖ్యలలో 3చే భాగింపబడు సంఖ్యల మొత్తం
= 12 + 15 + ……. + 999
= 3(4 + 5 + ……. + 333) = 3(1 + 2 + …….. + 333) – 3(1 + 2 + 3)
= 3 × 333 × \(\frac{(333+1)}{2}-\frac{3 \times 3(3+1)}{2}\)
= 3 × 333 × \(\frac{334}{2}-\frac{9 \times 4}{2}\)
= 999 × 167 – 9 × 2
= 166833 – 18 = 166815.