AP Board 8th Class Maths Solutions Chapter 8 జ్యామితీయ పటాల అన్వేషణ InText Questions

SCERT AP 8th Class Maths Solutions Chapter 8 జ్యామితీయ పటాల అన్వేషణ InText Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 8th Lesson జ్యామితీయ పటాల అన్వేషణ InText Questions

ఇవి చేయండి

1. క్రింది పటాలలో సర్వసమాన పటాల జతలను గుర్తించండి. (పేజీ నెం. 184)

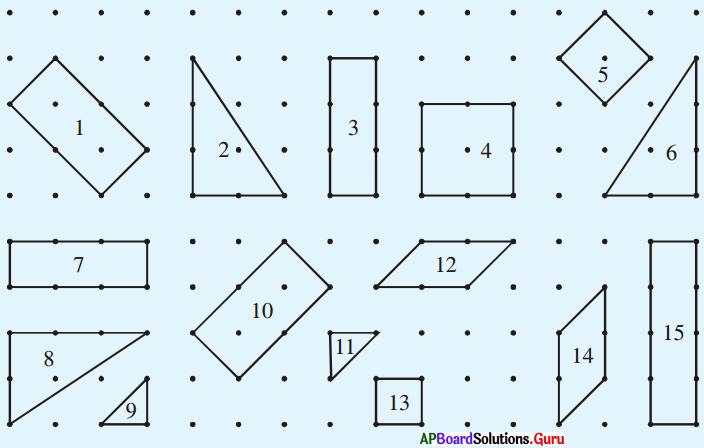
సాధన.
పై పటాలలో సర్వసమాన పటాల జతలు (1, 10), (2, 6, 8), (3, 7), (12, 14), (9, 11).

2. క్రింది పటాల జతలను గమనించండి. అవి సర్వసమానాలేమో తెల్పండి. కారణాలు వివరించండి. పటాలను పేర్లతో చెప్పండి. (పేజీ నెం. 185)


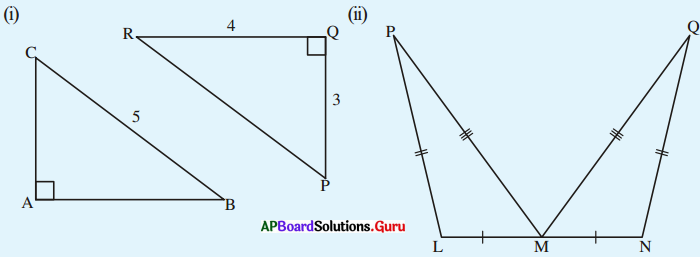
సాధన.
i) ΔABC, ΔPQRల నుండి
∠A = ∠Q (కోణాలు సమానాలు)
భుజాలు సమానాలు అని ఇవ్వలేదు. కాని ఆ రెండు పటాలను ఒకదానిపై ఒకటి ఉంచిన అవి ఏకీభవిస్తాయి.
∴ ΔABC ≅ ΔPQR

ii) ΔPLM, ΔQNM ల నుండి
PL = QN (భుజం)
LM = MN (భుజం)
PM = QM (భుజం)
పై రెండు త్రిభుజాలలో అనురూప భుజాలు సమానం.
∴ ΔPLM ≅ ΔQNM

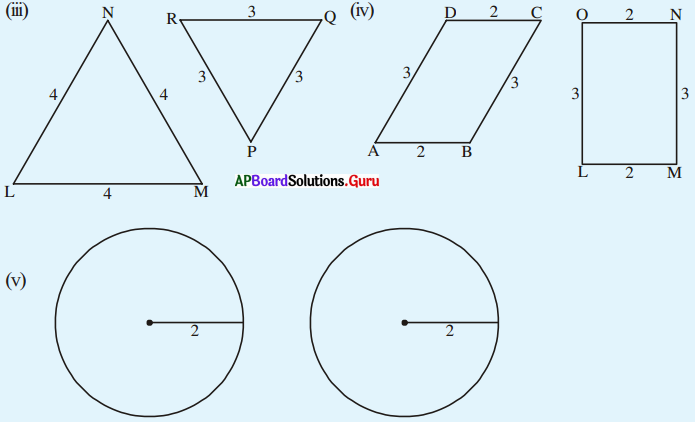
iii) ΔLMN, ΔPQR ల నుండి
NL ≠ PQ, LM ≠ QR, NM ≠ RP
∴ ΔLMN ≠ ΔPQR
(అనురూపకోణాలు ఇవ్వలేదు)

iv) ABCD ఒక సమాంతర చతుర్భుజం,
LMNO ఒక దీర్ఘచతురస్రం
దీర్ఘచతురస్రం మరియు సమాంతర చతుర్భుజం ఎప్పుడూ కూడా సర్వసమానాలు కాదు.

v) రెండు వృత్తాల నుండి
r₁ = r₂ = 2 యూ॥
రెండు వృత్తాలు సర్వసమానాలు.

3. క్రింది చిత్రాలలో మొదటి రేఖా చిత్రంతో సరూపంగా ఉన్న రేఖాచిత్రాలను గుర్తించండి. (పేజీ నెం. 186)

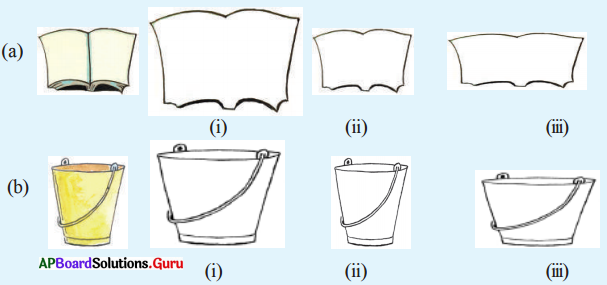
సాధన.
a) (ii)
b) (ii)

4. ఒక గ్రాఫ్ కాగితంపై ఒక త్రిభుజాన్ని గీచి సూచీ భిన్నం 3గా గల విస్తరణ పటాన్ని గీయండి. ఆ రెండు పటాలు సరూపాలేనా ? (పేజీ నెం. 191)
సాధన.
సోపానం 1 : ΔPQR ని నిర్మించి, త్రిభుజంపై లేని ఏదేని బిందువు ‘C’ ని విస్తరణ కేంద్రంగా గుర్తించుము. ‘C’ ని త్రిభుజ – శీర్షాలతో కలిపి ముందుకు పొడిగించుము.

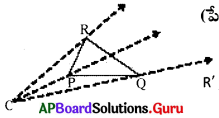
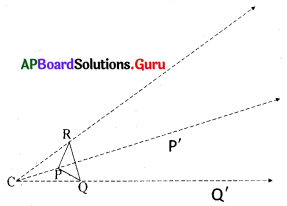
సోపానం 2 : వృత్తలేఖిని సహాయంతో పొడిగింపు రేఖలపై
CP’ = k (CP) = 3 CP
CQ’ = 3 CQ
CR’ = 3 CR
అగునట్లు P’, Q’ మరియు R’ బిందువులను గుర్తించుము.

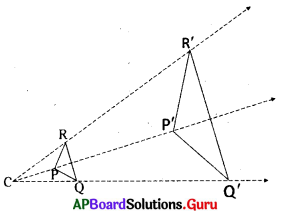
సోపానం 3 : P’Q’, Q’R’ మరియు R’P’ లను కలుపుము.
ΔP’Q’R’ ~ ΔPQR అని గమనించవచ్చు.

5. ఒక చతురస్రాన్ని గీచి సూచీ భిన్నాలు 4, 5 గా గల విస్తరణ పటాలను గీయండి. నీవేమి గమనించితివి ? అలాగే ఏదేని ఒక పటాన్ని పొడిగించండి. (పేజీ నెం. 191)
సాధన.
కొన్నిసార్లు మనం పటాలను వాటి వాస్తవ పరిమాణం కన్నా పెద్దదిగా వేయవలసి ఉంటుంది. ఉదాహరణకు సినిమా కటౌట్ (cut-outs) మీరు చూసి ఉంటారు. మరికొన్ని సార్లు పటాలను చిన్నవిగా గీయవలసి ఉంటుంది. ఉదాహరణకు నమూనాలు గీచే సందర్భంగా అసలు పరిమాణం కన్నా చిన్నవిగా గీస్తాము. అంటే మనం పటాల ఆకారాలను పెద్దవిగా కాని చిన్నవిగా కాని చేయవలసిన అవసరం నిత్యజీవితంలో ఏర్పడుతూ ఉంటుంది. ఈ విధంగా పెద్ద లేదా చిన్న సరూప పటాలు గీసే పద్ధతిని “సరూప విస్తరణం” అంటారు.

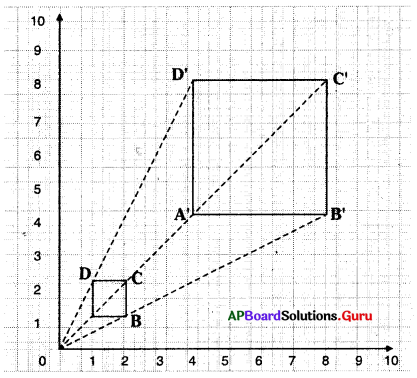
పటంలో ☐ ABCD విస్తరణను గమనించండి. ☐ ABCD ఒక చతురస్రం గ్రాఫ్ కాగితంపై గీయబడినది.
ప్రతి శీర్షాలు A, B, C మరియు D లు ‘O’ నుండి కలుపబడి వాటి 4 రెట్లు దూరాలకు వరుసగా A’, B’, C’ మరియు D’ వరకు పొడిగింపబడినవి. ఇప్పుడు A’, B’, C’,D’ లు కలుపగా ☐ ABCDకు 4 రెట్లు కొలతలు గల చతురస్రమును ఏర్పరచినవి. ఇక్కడ ‘O’ ను విస్తరణ కేంద్రం అని మరియు
\(\frac{\mathrm{OA}^{\prime}}{\mathrm{OA}}=\frac{4}{1}\) = 4 ను సూచీ భిన్నం (scale factor) అని అంటారు.
\(\frac{\mathrm{OA}^{\prime}}{\mathrm{OA}}=\frac{5}{1}\) = 5 ను సూచీ భిన్నం అంటారు.

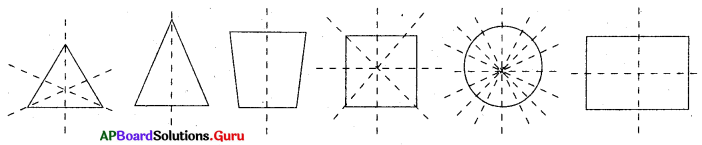
6. క్రింది ఆకారాలకు సాధ్యమైనన్ని సౌష్ఠవరేఖలు గీయండి. (పేజీ నెం. 193)

సాధన.

ప్రయత్నించండి

1. చాపిన చేతిలో ఒక స్కేలుని నిలువుగా పట్టుకొని మీ పాఠశాల భవనం ఏకీభవించునట్లు పాఠశాల నుండి దూరంగా జరుగుతూ సరిచేసుకొనుము. దీనికి సరిపడు పటాన్ని గీచి పాఠశాల భవనం ఎత్తుని అంచనా వేయండి. (పేజీ నెం. 189)
సాధన.
ఉదాహరణ ద్వారా వివరణ:
ఒక భవనం నుండి కొంత దూరములో గల బాలిక తనకెదురుగా గల పాఠశాల భవనం వైపు తన చేతిని చాపి ఒక స్కేలు పట్టుకొని నిలచి ఉన్నది. ఆమె తన చేతిలోని స్కేలు భవనముతో ఏకీభవించినట్లు పటంలో చూపినట్లు గమనించింది. ఈ వివరణను పై ఉదాహరణతో పోలిస్తే


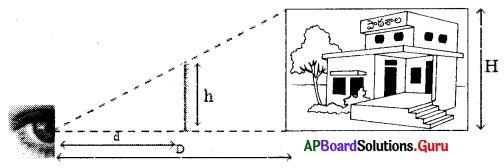
స్కేలు పొడవు, బాలిక చేతి పొడవు మరియు బాలిక నుండి భవనమునకు గల దూరములను కొలచి భవనం ఎత్తును అంచనా వేయవచ్చు.

2. a) కింది వానిలో బిందు సౌష్ఠవం గల వాటిని గుర్తించండి. (పేజీ నెం. 196)

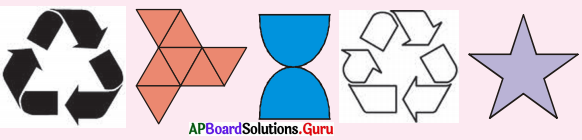
సాధన.
బిందు సౌష్ఠవం గల పటాలు (i), (ii), (iii), (v)

b) పై పటాలలో రేఖా సౌష్ఠవాన్ని కలిగిన పటాలు ఏవి ?
సాధన.
రేఖా సౌష్ఠవాన్ని కలిగిన పటాలు (i), (iii), (v)

c) రేఖా సౌష్ఠవమునకు మరియు బిందు సౌష్ఠవానికి మధ్యగల సంబంధమేమి ?
సాధన.
ఒక జ్యామితీయ పటానికి రేఖాసౌష్ఠవ అక్షాల సంఖ్య = బిందు సౌష్ఠవ పరిమాణం.

ఆలోచించి, చర్చించి వ్రాయుండి

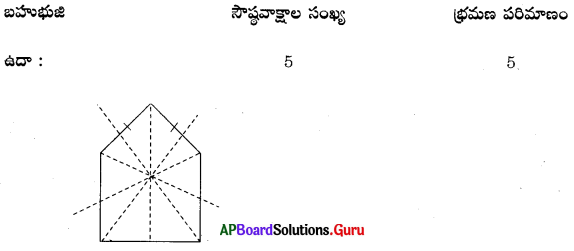
1. ఒక జ్యామితి పటం యొక్క సౌష్ఠవ అక్షాల సంఖ్యకు మరియు దాని భ్రమణ పరిమాణానికి మధ్యగల సంబంధం ఏమిటి ? (పేజీ నెం. 195)
సాధన.
ఒక పటానికి మధ్యగా ఒక రేఖను గీచిన ఆ రేఖకు ఇరువైపులా గల భాగాలు ఒకే విధంగా ఉండి ఒకదానిని ఒకటి ఏకీభవిస్తే ఆ రేఖ ఆ పటానికి సౌష్ఠవ అక్షం అంటారు. భ్రమణ పరిమాణం అనగా ఎన్నిసార్లు ఒక ఆకారాన్ని భ్రమణం చేసి తిప్పగా అది మళ్ళీ మొదటి ఆకారాన్ని పొందుతుందో ఆ సంఖ్యను భ్రమణ పరిమాణం అంటారు.

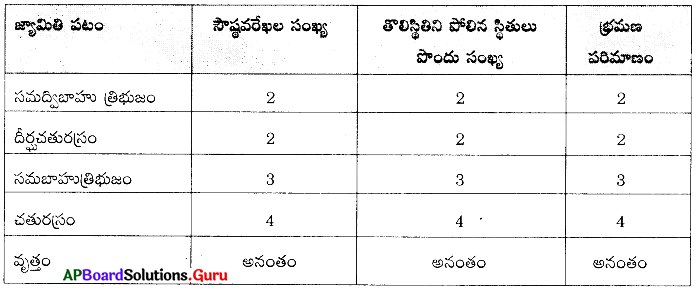
∴ పై పట్టికను అనుసరించి ఒక జ్యామితి పటం యొక్క సౌష్ఠవ రేఖల సంఖ్య = భ్రమణ పరిమాణం అగును.

2. ఒక క్రమ బహుభుజికి గల సౌష్ఠవ అక్షాల సంఖ్య ఎంత ? ఒక క్రమ బహుభుజి భుజాల సంఖ్యకు మరియు దాని భ్రమణ సౌష్ఠవ పరిమాణమునకు మధ్యగల సంబంధమేమి ? (పేజీ నెం. 195)
సాధన.
ఒక క్రమ బహుభుజి యొక్క భుజాల సంఖ్య ‘n’ అయిన దాని సౌష్ఠవాక్షాల సంఖ్య ‘n’ అవుతుంది. అదేవిధంగా దాని భ్రమణ పరిమాణం కూడా ‘n’ అవుతుంది.