AP Board 9th Class Maths Solutions Chapter 1 Real Numbers InText Questions

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 1 Real Numbers InText Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 1st Lesson Real Numbers InText Questions

Do This

Question 1.
Represent \(\frac{-3}{4}\) on a number line. (Page No.3)
Solution:

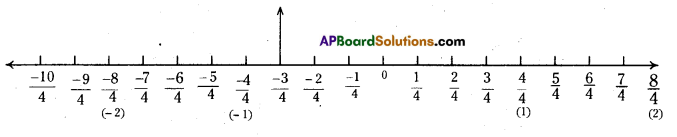
Step – 1: Divide each unit into four equal parts to the right and left side of zero on the number line.
Step – 2 : Take 3 parts after zero on its left side.
Step -3 : It represents \(\frac{-3}{4}\)

Question 2.
Write 0, 7, 10, -4 in p/q form (Page No.2)
Solution:

Question 3.
Guess my number : Your friend chooses an integer between 0 and 100. You have to find out that number by asking questions, but your friend can only answer ‘Yes’ or ‘No’. What strategy would you use ? (Page No.3)
Solution:
Let my friend choosen 73; then my questions may be like this.

Q : Does it lie in the first 50 numbers ?
A: No .

Q : Does it lie between 50 and 60 ?
A: No

Q : Does it lie between 60 and 70 ?
A: No

Q : Does it lie between 70 and 80 ?
A: Yes
[then my guess would be “it is a number from 70 to 80]

Q : Is it an even number ?
A: No
[my guess : it should be one of the numbers 71, 73, 75, 77 and 79]

Q : Is it a prime number ?
A: Yes
[my guess : it may be 71, 73 or 79]

Q : Is it less than 75 ?
A: Yes
[my guess : it may be either 71 or 73]

Q : Is it less than 72 ?
A: No

Then the number is 73.
Therefore the strategy is
→ Use number properties such as even, odd, composite or prime to determine the number.

Do This

Question (i)
Find five rational numbers between 2 and 3 by mean method. (Page No.4)
Solution:
We know that \(\frac{a+b}{2}\) is a rational
between any two numbers a and b.
Let a = 2 and b = 3

Question (ii)
Find 10 rational numbers between \(\frac{-3}{11}\) and \(\frac{8}{11}\) (Page No.4)
Solution:
\(\frac{-3}{11}<\left[\frac{-2}{11}, \frac{-1}{11}, \frac{0}{11}, \frac{1}{11}, \frac{2}{11}, \frac{3}{11}, \frac{4}{11}, \frac{5}{11}, \frac{6}{11}, \frac{7}{11}\right]<\frac{8}{11}\)

Do This

Question
Find the decimal form of
(i) \(\frac{1}{17}\) (Page No.5)
Solution:

\(\frac{1}{19}\) = 0.052631

(ii) \(\frac{1}{19}\)(Page No.5)
Solution:

Try These

Question 1.
Find the decimal values of the following. (Page No.6)
Solution:
i) \(\frac{1}{2}\) = 0.5
ii) \(\frac{1}{2^{2}}=\frac{1}{4}\) = 0.25
iii) \(\frac{1}{5}\) = 0.2
iv) \(\frac{1}{5 \times 2}=\frac{1}{10}\) = 0.1
v) \(\frac{3}{10}\) = 0.3
vi) \(\frac{27}{25}\)

vii) \(\frac{1}{3}\)
Solution:

viii) \(\frac{7}{6}\)
Solution:

ix) \(\frac{5}{12}\)
Solution:

x) \(\frac{1}{7}\)
Solution:

Think, Discuss and Write

Question 1.
Kruthi said √2 can be written as \(\frac{\sqrt{2}}{1}\) which is in form. So √2 is a rational number. Do you agree with her argument ? (Page No.10)
Solution:
No.
Writing √2 = \(\frac{\sqrt{2}}{1}\) is not in the \(\frac { p }{ q }\) form.
Since p and q are integers and √2 is not an integer.

Try These

Question 1.
Find the value of √3 upto six decimals.(Page No.10)
Solution:

Step 1 :
Write 3 as 3.00 00 00 00 00 00 00
Step – 2 :
Group the zeros in pairs (i.e.) make periods.
Step – 3 :
Find the square root using long division method.
∴ √3 = 1.732050

Try These

Question 1.
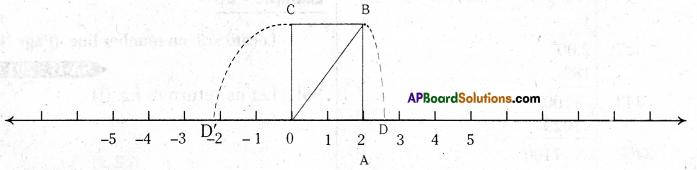
Locate √5 and -√5 on the number line [Hint 5 = 2² + 1²](Page No.12)
Solution:
Step – 1 :
At zero draw a rectangle of length 2 units and breadth 1 unit.

Step – 2 :

Step – 3 :
Using compass draw an arc of radius OB with centre ‘O’ which cuts the num-ber line at D and D¹.

Step – 4 :
D represents √5 and D¹ represents – √5 on the number line.

Activity

Question
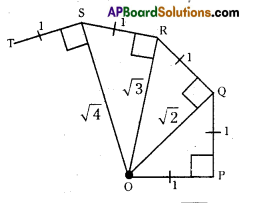
Constructing the ‘Square root spiral’. (Page No. 15)
Solution:
Take a large sheet of paper and construct the ‘Square root spiral’ in the following manner.
Step – 1 : Start with point ‘O’ and draw a line segment \(\overline{\mathrm{OP}}\) of 1 unit length.
Step – 2 : Draw a line segment \(\overline{\mathrm{PQ}}\) perpendicular to \(\overline{\mathrm{OP}}\) of unit length (where OP = PQ = 1) (see Fig.)
Step – 3 : Join 0, Q. (OQ = √2 )
Step – 4 : Draw a line segment OR of unit length perpendicular to \(\overline{\mathrm{OQ}}\)
Step – 5 : Join O, R. (OR = √3 )
Step – 6 : Draw a line segment RS of unit length perpendicular to \(\overline{\mathrm{OR}}\).
Step – 7 : Continue in this manner for some more number of steps, you will create a
beautiful spiral made of line segment \(\overline{\mathrm{PQ}}, \overline{\mathrm{QR}}, \overline{\mathrm{RS}}, \overline{\mathrm{ST}}, \overline{\mathrm{TU}}\) …………etc. Note that the line segments \(\overline{\mathrm{OQ}}, \overline{\mathrm{OR}}, \overrightarrow{\mathrm{OS}}, \overline{\mathrm{OT}}, \overline{\mathrm{OU}}\) …… etc., denote the lengths √2,√3, √4, √5, √6 respectively.

Do This

Question 1.
Find rationalising factors of the denominators of (Page No. 20)
i) \(\frac{1}{2 \sqrt{3}}\)
Solution:
\(\frac{1}{2 \sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}=\frac{\sqrt{3}}{2 \times 3}=\frac{\sqrt{3}}{6}\)
∴ The R.F is √3

ii) \(\frac{1}{\sqrt{5}}\)
Solution:
\(\frac{3}{\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}}=\frac{3 \sqrt{5}}{5}\)
∴ The R.F is √5

iii) \(\frac{1}{\sqrt{8}}\)
Solution:

Do This;

Question
Simplify : (Page No. 23)

i) (16) ^1/2
Solution:
(16)^1/2 = (4 x 4)^1/2 = (42)^1/2 = 4^2/2 = 4

ii) (128)^1/7
Solution:
(128)^1/7 =(2 X 2 X 2 X 2 X 2 X 2 X 2)^1/7 = (2⁷)^1/7 = 2

iii) (343)^1/5
Solution:
(343)^1/5= (3 x 3 x 3 x 3 x 3)^1/5 = (3⁵)^1/5= 3

Question 1.
Write the following surds in exponen-tial form (Page No. 24)
i) √2
Solution:
√2 = 2^1/2

ii) 3√9
Solution:
\(\sqrt[3]{9}=\sqrt[3]{3 \times 3}=\sqrt[3]{3^{2}}=3^{\frac{2}{3}}\)

iii) \(\sqrt[5]{20}\)
Solution:
\(\begin{aligned}
\sqrt[5]{20}=\sqrt[5]{2 \times 2 \times 5} &=\sqrt[5]{2^{2} \times 5} \\
&=2^{\frac{2}{5}} \times 5^{\frac{1}{5}}
\end{aligned}\)

iv) 17√19
Solution:
\(\sqrt[17]{19}=19^{\frac{1}{17}}\)

Question 2.
Write the surds in radical form. (Page No. 24)
i) 5^1/7 = \(\sqrt[7]{5}\)
ii) 17^1/6 = \(\sqrt[6]{17}\)
iii) 5^2/5 = \(\sqrt[5]{5^{2}}=\sqrt[5]{5 \times 5}=\sqrt[5]{25}\)
iv) 142^1/2 = \(\sqrt{142}\)