AP State Syllabus AP Board 9th Class Maths Solutions Chapter 15 Proofs in Mathematics Ex 15.4 Textbook Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 15th Lesson Proofs in Mathematics Exercise 15.4
![]()
Question 1.
State which of the following are mathematical statements and which are not ? Give reason.
i) She has blue eyes.
Solution:
This is not a mathematical statement. no mathematics is involved in it.
ii) x + 7 = 18
Solution:
This is not a statement, as its truthness cant be determined.
iii) Today is not Sunday.
Solution:
This is not a statement. This is an am biguous open sentence.
iv) For each counting number x, x + 0 = x.
Solution:
This is a mathematical statement.
![]()
v) What tune is it?
Solution:
This is not a riathematical statement.
Question 2.
Find counter examples to disprove the following statements.
i) Every rectangle is a square.
Solution:

A rectangle and square are equiangular i.e., all the four angles are right angles. This doesn’t mean that they have equal sides.
ii) For any integers x and y,
\(\sqrt{x^{2}+y^{2}}\) = x + y
Solution:
Let x = 3; y = 8
\(\sqrt{x^{2}+y^{2}}=\sqrt{3^{2}+8^{2}}\)
= \(\sqrt{9+64}=\sqrt{73}\)
x + y = 3 + 8 = 11
Here, √73 ≠ 11
i.e., \(\sqrt{x^{2}+y^{2}}\) ≠ x + y
iii) If n is a whole number then 2n2 +11 is a prime.
Solution:
If n = 11 then 2n2+ 11 = 2 (11)2 + 11
= 11 (2 × 11 + 1) = 11 × (22 + 1)
= 11 × 23 is not a prime.
![]()
iv) Two triangles are congruent if all their corresponding angles are equal.
Solution:
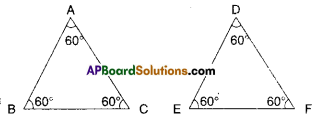
If the corresponding angles are equal then the triangles are only similar.
v) A quadrilateral with all sides are equal is a square.
Solution:
A rhombus is not a square, but all its sides are equal.
Question 3.
Prove that the sum of two odd numbers is even.
Solution:
| Steps | Reasons |
| 1) (2m + 1); (2n + 1) be the two odd numbers | General form of an odd number. |
| 2) (2m + 1) + (2n + 1) = (2m + 2n + 2) = 2 (m + n + 1) = 2K Hence proved. |
Adding the two numbers General form of an even number. |
![]()
Question 4.
Prove that the product of two even numbers is an even number.
Solution:
| Steps | Reasons |
| 1) Let 2m and 2n be two even numbers. | General form of an even number. |
| 2) 2m.2n = 4mn = 2(2mn) = 2K | Taking the product Rearranging the numbers. |
| 3) 2K where K = 2mn | K=2mn |
| 4) Even number Hence proved. |
General form of an even number. |
Question 5.
Prove that if x is odd, then x2 is also odd.
Solution:
Let x be an odd number.
Then x = 2m + 1
(general form of ah odd number) Squaring on both sides,
x2 = (2m + 1)2
= 4m2 + 4m +1
= 2 (2m2 + 2m) + 1
= 2K + 1 where K = 2m2+ 2
Hence x2 is also odd.
![]()
Question 6.
Examine why they work ?
Choose a number. Double it. Add nine. Add your original number. Divide by three. Add four. Subtract your original number. Your result is seven.
Solution:
Choose a number = x say
Double it = 2x
Add nine = 2x + 9
Add your original number
= 2x + 9 + x = 3x + 9
Divide by 3 = (3x + 9) ÷ 3
= \(\frac{3 x}{3}+\frac{9}{3}\) = x + 3
Add 4 ⇒ x + 3 + 4 = x + 7
Subtract your original number =
x + 7 – x = 7
Your result is 7 – True.
![]()
ii) Write down any three digit number (for example, 425). Make a six digit number by repeating these digits in the same order 425425. Your new number is divisible by 7, 11 and 13.
Solution:
Let a three digit number be xyz.
Repeat the digit = xyzxyz
= xyz × (1001)
= xyz × (7 × 11 × 13)
Hence the given conjecture is true.