AP Board 9th Class Maths Solutions Chapter 2 Polynomials and Factorisation Ex 2.4

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 2 Polynomials and Factorisation Ex 2.4 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 2nd Lesson Polynomials and Factorisation Exercise 2.4

Question 1.
Determine which of the following polynomials has (x + 1) as a factor.
i) x³ – x² – x + 1
Solution:
f(- 1) = (- 1)³ – (- 1)² – (- 1) + 1
= -1 – 1 + 1 + 1 = 0
∴ (x + 1) is a factor.

ii) x⁴ -x³ +x² – x + 1
Solution:
f(- 1) = (- 1)⁴ – (- 1)³ + (- 1)² – (- 1) + 1
= 1 + 1 + 1 + 1 + 1= 5
∴ (x + 1) is not a factor.

iii) x⁴ + 2x³ + 2x² + x + 1
Solution:
f(- 1) = (-1)⁴ + 2 (- 1)³ + 2 (- 1)² + (-1) + 1
= 1 – 2 + 2 – 1 + 1 = 1
∴ (x + 1) is not a factor.

iv) x³ – x² – (3 – √3)x + √3
Solution:
f(- 1) = (- 1)³ – (- 1)² – (3 – √3)(-1) + √3
= – 1 – 1 + 3 – √3 + √3 = 1
∴ (x + 1) is not a factor.

Question 2.
Use the factor theorem to determine whether g(x) is a factor of f(x) in each of the following cases:
i) f(x) = 5x³ + x² – 5x – 1; g(x) = x + 1
[Factor theorem : If f(x) is a polynomial; f(a) = 0 then (x – a) is a factor of f(x); a ∈ R]
Solution:
g(x) = x+ 1 = x- a say
∴ a = – 1
f(a) = f(- 1) = 5 (- 1)³ + (- 1)² – 5 (- 1) – 1
= -5 + 1 + 5 – 1 = 0
∴ x + 1 is a factor of f(x).

ii) f(x) = x³ + 3x² + 3x + 1; g(x) = x + 1
Solution:
g(x) = x + 1 = x – a
∴ a = – 1
f(a) = f(- 1) = (- 1)³ + 3 (- 1)² + 3(-1) + 1
= -1 + 3 – 3 + 1 =0
∴ f(x) is a factor of g(x).

iii) f(x) = x³ – 4x² + x + 6;
g(x) = x – 2
Solution:
g(x) = x- 2 = x- a
∴ a = 2
f(a) = f(2) = 2³ – 4(2)² + 2 + 6
= 8 – 16 + 2 + 6 = 0
∴ g(x) is a factor of f(x).

iv) f(x) = 3x³+ x² – 20x +12; g(x) = 3x – 2
Solution:
g(x) = 3x – 2 = \(x-\frac{2}{3}\) = x – a
∴ a = 2/3

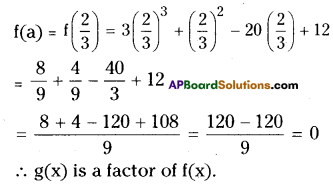
v) f(x) = 4x³+ 20x²+ 33x + 18; g(x) = 2x + 3
Solution:
g(x) = 2x + 3 = x + \(\frac{3}{2}=\) = x – a
∴ a = -3/2

∴ g(x) is a factor of f(x).

Question 3.
Show that (x – 2), (x + 3) and (x – 4) are factors of x³ – 3x² – 10x + 24.
Solution:
Given f(x) = x³ – 3x² – 10x + 24
To check whether (x – 2), (x + 3) and (x – 4) are factors of f(x), let f(2), f(- 3) and f(4)
f(2) = 2³ – 3(2)² – 10(2) + 24
= 8- 12-20 + 24 = 0
∴ (x – 2) is a factor of f(x).

f(- 3) = (- 3)³ – 3(- 3)²– 10(- 3) + 24
= – 27 – 27 + 30 + 24 = 0
∴ (x + 3) is a factor of f(x).

f(4) = (4)³ – 3 (4)² – 10 (4) + 24
= 64 – 48 – 40 + 24
= 88 – 88
= 0
∴ (x – 4) is a factor of f(x).

Question 4.
Show that (x + 4), (x – 3) and (x – 7) are factors of x³ – 6x² – 19x + 84.
Solution:
Let f(x) = x³ – 6x² – 19x + 84
To verify whether (x + 4), (x – 3) and (x – 7) are factors of f(x) we use factor theorem.

Let f(- 4), f(3) and f(7)
f(- 4) = (- 4)³ – 6 (- 4)² – 19 (- 4) + 84
= -64 – 96 + 76 + 84
= 0 .
∴ (x + 4) is a factor of f(x).

f(3) = 3³ – 6(3)² – 19(3) + 84
= 27 – 54 – 57 + 84
= 0
∴ (x – 3) is a factor of f(x).

f(7) = 7³ – 6(7)² – 19(7) + 84
= 343 – 294 – 133 + 84
= 427 – 427
= 0
∴ (x – 7) is a factor of f(x).

Question 5.
If both (x – 2) and \(\left(x-\frac{1}{2}\right)\) of px² + 5x + r, show that p = r.
Solution:
Let f(x) = px²+ 5x + r
As (x – 2) and \(\left(x-\frac{1}{2}\right)\) are factor of f(x), we have f(2) = 0 and f(1/2) = 0
∴ f(2) = p(2)² + 5(2) + r
= 4p + 10 + r = 0
= 4p + r
= – 10 ………………(1)

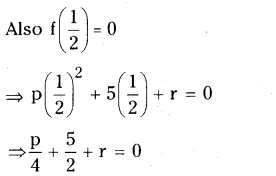
⇒ p + 10 + 4r = 0
⇒ p + 4r = – 10 ………………. (2)
From (1) and (2);
4p + r = p + 4r
4p – p = 4r – r
3p = 3r
∴ P = r

Question 6.
If (x² – 1) is a factor of ax⁴ + bx³ + cx² + dx + e, show that a + c + e = b + d = 0.
Solution:
Let f(x) = ax⁴ + bx³ + cx² + dx + e
As (x – 1) is a factor of f(x) we have
x² – 1 = (x + 1) (x – 1) hence f(1) = 0 and f(-1) = 0
f(1) = a + b + c + d + e = 0 ……………. (1)
and f(-1) = a- b + c- d + e = 0
⇒ a + c + e = b + d
Substitute this value in equation (1)
a + c + e + b + d=0
b + d + b + d=0
2 (b + d) = 0
⇒ b + d = 0
∴ a + c + e = b + d = 0

Question 7.
Factorise
i) x³ – 2x² – x + 2
Solution:
Let f(x) = x³ – 2x² – x + 2
By trial, we find f(l) = 1³ – 2(1)² – 1 + 2
= 1 – 2 – 1 + 2
= 0 .
∴ (x – 1) is a factor of f(x).
[by factor theorem]
Now dividing f(x) by (x – 1).

f(x) = (x – 1) (x² – x – 2)
= (x – 1) [x² – 2x + x- 2]
= (x – 1) [x (x – 2) + 1 (x – 2)]
= (x – 1) (x – 2) (x + 1)

ii) x³ – 3x² – 9x – 5
Solution:
Let f(x) = x³ – 3x² – 9x – 5By trial,
f(- 1) = (- 1)³ – 3(- 1)² – 9(- 1) – 5
=-1 – 3 + 9 – 5
=0
∴ (x + 1) is a factor of f(x).
[ ∵ by factor theorem]
Now dividing f(x) by (x + 1).

f(x)=(x + 1)(x² – 4x – 5)
But x²– 4x – 5 = x² – 5x + x – 5
= x (x – 5) + 1 (x – 5)
=(x – 5)(x + 1)
∴ f(x)=(x + 1)(x + 1)(x – 5)

iii) x³ + 13x² + 32x + 20
Solution:
Let f(x) = x³ + 13x² + 32x + 20
Let f(- 1)
= (- 1)³ + 13 (- 1)² + 32 (- 1) + 20
= – 1 + 13 – 32 + 20 = 33 – 33 = 0
∴ (x + 1) is a factor of f(x).
[ ∵ by factor theorem] Now dividing f(x) by (x + 1).

iv) y³ + y² – y – 1
Let f(y) = y³ + y² – y – 1
f(1) = 1³+ 1²– 1 – 1 = 0
(y – 1) is a factor of f(y).
Now dividing f(y) by (y – 1).

∴ f(x) = (x + 1)(x² + 12x + 20)
But (x² + 12x + 20) = x²+ 10x + 2x + 20
=x(x + 10)+2(x + 10)
=(x + 10)(x + 2)
∴f(x) = (x + 1)(x + 2)(x + 10)

Question 8.
If ax² + bx + c and bx² + ax + c have a common factor x + 1 then show that c = 0 and a = b.
Solution:
Let f(x) = ax² + bx + c and g(x) = bx² + ax + c given that (x + 1) is a common factor for both f(x) and g(x).
∴ f(-1) = g(- 1)
⇒a(- 1)² + b(- 1) + c
= b(- 1)² + a (- 1) + c
⇒ a – b + c = b – a + c
⇒ a + a = b + b
⇒ 2a = 2b
⇒ a = b
Also f(- 1) = a – b + c = 0
⇒ b – b + c = 0
⇒ c = 0

Question 9.
If x² – x – 6 and x² + 3x – 18 have a common factor x – a then find the value of a.
Solution:
Let f(x) = x² – x – 6 and
g(x) = x² + 3x – 18
Given that (x – a) is a factor of both f(x) and g(x).
f(a) = g(a) = 0
⇒ a² – a – 6 = a² + 3a – 18
⇒ – 4a = – 18 + 6
⇒ – 4a = – 12
∴ a = 3

Question 10.
If (y – 3) is a factor of y³– 2y²– 9y + 18, then find the other two factors.
Solution:
Let f(y) = y³– 2y² – 9y + 18
Given that (y – 3) is a factor of f(y).
Dividing f(y) by (y – 3)

∴ f(y) = (y – 3) (y + y – 6)
But y² + y – 6
= y² + 3y – 2y – 6
= y (y + 3) – 2 (y + 3)
= (y + 3) (y – 2)
∴ f(y) = (y – 2)(y – 3)(y + 3)
The other two factors are (y – 2) and (y + 3).