AP State Syllabus AP Board 9th Class Maths Solutions Chapter 7 Triangles Ex 7.2 Textbook Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 7th Lesson Triangles Exercise 7.2
Question 1.
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at ‘O’. Join A to O. Show that (i) OB = OC (ii) AO bisects ∠A.
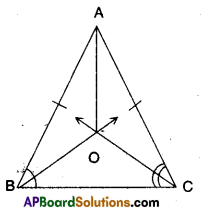
Solution:
Given that in ΔABC
AB = AC
Bisectors of ∠B and ∠C meet at ‘O’.
To prove
i) OB = OC
∠B = ∠C (Angles opposite to equal, sides)
\(\frac{1}{2} \angle \mathrm{B}=\frac{1}{2} \angle \mathrm{C}\) (Dividing both sides by 2)
∠OBC = ∠OCB
⇒ OB = OC (∵ Sides opposite to equal angles in ΔOBC)
ii) AO bisects ∠A.
In ΔAOB and ΔAOC
AB = AC (given)
BO = CO (already proved)
∠ABO = ∠ACO (∵ ∠B =∠C)
∴ ΔAOB ≅ ΔAOC
⇒ ∠BAO = ∠CAO [ ∵ CPCT of ΔAOB and ΔAOC]
∴ AO is bisector of ∠A.
![]()
Question 2.
In ΔABC, AD is the perpendicular bisector of BC (see given figure). Show that ΔABC is an isosceles triangle in which AB = AC
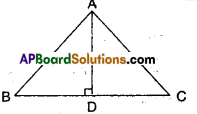
Solution:
Given that AD ⊥ BC; AD = DC
In ΔABD and ΔACD
AD = AD (common)
BD = DC (given)
∠ADB = ∠ADC (given)
∴ ΔABD ≅ ΔACD (∵ SAS congruence)
⇒ AB = AC (CPCT of ΔABD and ΔACD)
![]()
Question 3.
ABC is an isosceles triangle in which altitudes BD and CE are drawn to equal sides AC and AB respectively (see figure). Show that these altitudes are equal.
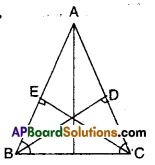
Solution:
Given that AC = AB; BD ⊥ AC; CE ⊥ AB
In ΔBCD and ΔCBE
∠BDC = ∠CEB (90° each)
∠BCD = ∠CBE (∵ angles opp. to equal sides of a triangle)
BC = BC
∴ ΔBCD ≅ ΔCBE (∵ AAScongruence)
⇒ BD = CE (CPCT)
![]()
Question 4.
ABC is a triangle in which altitudes BD and CE to sides AC and AB are equal (see figure). Show that
i) ΔABD ≅ ΔACE
ii) AB = AC i.e., ABC is an isosceles triangle.
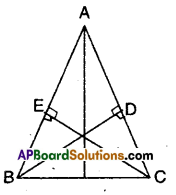
Solution:
Given that BD ⊥ AC; CE ⊥ AC
BD = CE
Now in ΔABD and ΔACE
∠ADB = ∠AEC (∵ given 90°)
∠A = ∠A (commori angle)
BD = CE
∴ ΔABD = ΔACE (∵ AAS congruence)
⇒ AB = AC (∵ C.P.C.T)
![]()
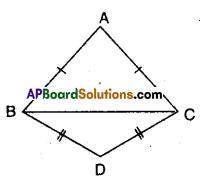
Question 5.
ΔABC and ΔDBC are two isosceles triangles on the same base BC (see figure). Show that ∠ABD = ∠ACD.
Solution:
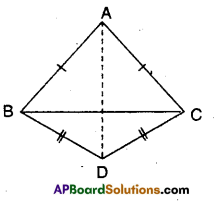
Given that ΔABC and ΔDBC are isosceles.
To prove ∠ABD = ∠ACD
Join A and D.
Now in ΔABD and ACD
AB = AC (∵ equal sides of isosceles triangles)
BD = CD (∵ equal sides of isosceles triangles)
AD = AD (∵ common side)
∴ ΔABD ≅ ΔACD (∵ SSS congruence)
⇒ ∠ABD = ∠ACD (CPCT)