AP State Syllabus AP Board 9th Class Maths Solutions Chapter 7 Triangles Ex 7.4 Textbook Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 7th Lesson Triangles Exercise 7.1
Question 1.
Show that in a right angled triangle, the hypotenuse is the longest side.
Solution:
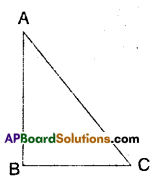
Let a ΔABC be right angled at ∠B.
Then ∠A + ∠C = 90°
(i.e.,) ∠A and ∠C are both acute.
Now, ∠A < ∠B ⇒ BC < AC
Also ∠C < ∠B ⇒ AB < AC
∴ AC, the hypotenuse is the longest side.
![]()
Question 2.
In the given figure, sides AB and AC of ΔABC are extended “to points P and Q respectively. Also ∠PBC < ∠QCB. Show that AC > AB.
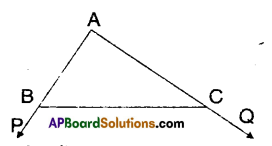
Solution:
From the figure,
∠PBC = ∠A + ∠ACB
∠QCB = ∠A + ∠ABC
Given that ∠PBC < ∠QCB
⇒∠A + ∠ACB < ∠A + ∠ABC
⇒ ∠ACB < ∠ABC
⇒ AB < AC
⇒ AC > AB
Hence proved.
![]()
Question 3.
In the given figure, ∠B < ∠A and ∠C < ∠D. Show that AD < BC.

Solution:
Given that ∠B < ∠A; ∠C < ∠D
∠B < ∠A ⇒ AO < OB [in ΔAOB] ……………… (1)
∠C < ∠D ⇒ OD < OC [in ΔCOD]…… (2)
Adding (1) & (2)
AO + OD < OB + OC
AD < BC
Hence proved.
![]()
Question 4.
AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see figure). Show that ∠A >∠C and ∠B > ∠D.
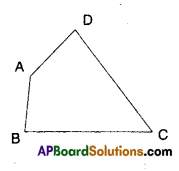
Solution:
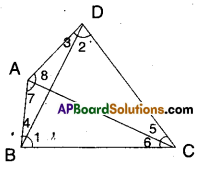
Given that AB and CD are the smallest and longest sides of quadrilateral ABCD.
From the figure,
In ΔBCD
∠1 > ∠2 [∵ DC > BC] ………………(1)
In ΔBDA
∠4 > ∠3 [∵ AD > AB] ………….(2)
Adding (1) & (2)
∠1 + ∠4 > ∠2 + ∠3
∠B > ∠D
Similarly,
In ΔABC, ∠6 < ∠7 [ ∵AB < BC] ……………….(3)
In ΔACD
∠5 < ∠8 …………. (4)
Adding (3) & (4)
∠6 + ∠5 < ∠7 + ∠8
∠C < ∠A ⇒ ∠A > ∠C
Hence proved.
![]()
Question 5.
In the given figure, PR > PQ and PS bisects ∠QPR. Prove that
∠PSR > ∠PSQ.
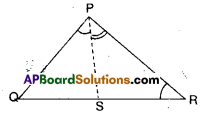
Solution:
Given that PR > PQ;
∠QPS =∠RPS
PR> PQ
∠Q > ∠R
Now ∠Q +∠QPS > ∠R + ∠RPS
⇒ 180° – (∠Q + ∠QPS) < 180° – (∠R + ∠RPS)
⇒ ∠PSQ < ∠PSR ⇒ ∠PSR > ∠PSQ
Hence proved.
Question 6.
If two sides of a triangle measure 4 cm and 6 cm find all possible measurements (positive integers) of the third side. How many distinct triangles can be obtained ?
Solution:
Given that two sides of a triangle are 4 cm and 6 cm.
∴ The measure of third side > Differ-ence between other two sides.
third side > 6 – 4
third side > 2
Also the measure of third side < sum of other two sides
third side <6 + 4 < 10
∴ 2 < third side <10
∴ The measure of third side may be 3 cm, 4 cm, 5 cm, 6 cm, 7 cm, 8 cm, 9 cm
∴ Seven distinct triangles can be obtained.
![]()
Question 7.
Try to construct a triangle with 5 cm, 8 cm and 1 cm. Is it possible or not ? Why ? Give your justification.
Solution:
As the sum (6 cm) of two sides 5 cm and 1 cm is less than third side. It is not possible to construct a triangle with the given measures.