AP State Syllabus AP Board 9th Class Maths Solutions Chapter 7 Triangles InText Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 7th Lesson Triangles InText Questions
![]()
Do This
Question 1.
There are some statements given below. Write whether they are true or false. [Page No. 150]
Solution:
i) Two circles are always congruent. – False
ii) Two line segments of same length are always congruent. – True
iii) Two right angle triangles are some times congruent. – True
iv) Two equilateral triangles with their sides equal are always congruent. – True
Question 2.
Which minimum measurements do you require to check if the given figures are congruent? [Page No. 150]
i) Two rectangles.
Solution:
Length and breadth are required.
ii) Two rhombuses.
Solution:
One side and one interior angle are required.
![]()
Do These
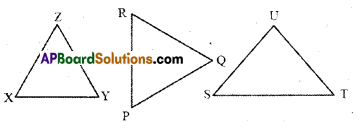
Question 1.
State whether the following triangles are congruent or not. Give reasons for your answer. [Page No. 153]
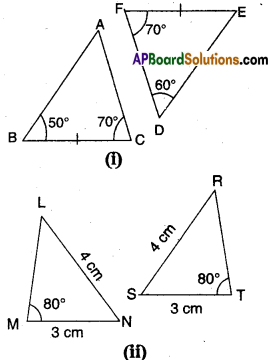
Solution:
i) ΔABC ≅ ΔDEF
∵ ∠B = ∠E (∵ Angle sum property Z E = 180° – (70° + 60°) = 50°)
BC = EF
∠C = ∠F
∴ By SAS congruence
ΔABC ≅ ΔDEF
ii) In ΔMNL and ΔTSR
MN = ST
NL = TR
∠ M = ∠ T (∵ ΔMNL is flipped to get ΔTSR)
∴ ΔMNL ≅ ΔTSR
![]()
Question 2.
In the given figure, the point P bisects AB and DC. Prove that ΔAPC ≅ ΔBPD. [Page No. 153]
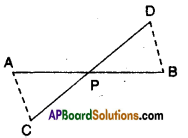
Solution:
Given that P bisects AB and DC.
Now in ΔAPC and ΔBPD
AP = BP (∵ P bisects AB)
CP = DP (∵ P bisects CD)
∠ APC = ∠ BPD
∴ ΔAPC ≅ ΔRPP (∵ SAS congruence)
Activity
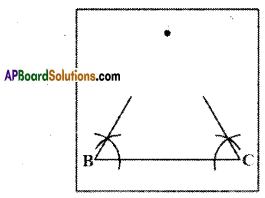
1. On a tracing paper draw a line segment BC of length 6 cm.
2. From vertices B and C draw rays with angle 600 each. Name the point A where they meet
3. Fold the paper so that B and C fit precisely on top of each other. What do you observe? Is AB = AC?
[Page No. 160]
![]()
Do This
Question 1.
In the figure given below ΔABC and ΔDBC are two triangles such that \(\overline{\mathbf{A B}}=\overline{\mathbf{B D}}\) and \(\overline{\mathbf{A C}}=\overline{\mathbf{C D}}\) . Show that ΔABC ≅ ΔDBC [Page No. 164]
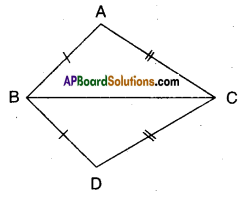
Solution:
Given that \(\overline{\mathbf{A B}}=\overline{\mathbf{B D}}\) and \(\overline{\mathbf{A B}}=\overline{\mathbf{B D}}\)
In ΔABC and ΔDBC
AB = BD (∵ given)
AC = DC (∵ given)
BC = BC (common side)
∴ ΔABC ≅ ΔDBC
( ∵ by SSS congruence)
![]()
Activity
Question 1.
Construct a right angled triangle with hypotenuse 5 cm. and one side 3 cm. long. How many different triangles can be constructed? Compare your triangle with those of the other members of your class. Are the triangles congruent? Cut them out and place one triangle over the other with equal side placed on each other. Turn the triangle if necessary what do you observe? You will find that two right triangles are congruent, if side and hypotenuse of one triangle are respectively equal to the corresponding side and hypotenous of other triangle.
[Page No. 165]
Activity
Question 1.
Draw a triangle ABC mark a point A’ on CA produced (new position of it)
So A’C > AC (Comparing the lengths) Join A to B and complete the triangle ABC.
What can you say about ∠A’BC and ∠ABC ?
Compare them. What do you observe?
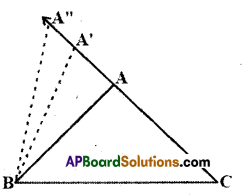
Clearly, ∠A’BC > ∠ABC Continue to mark more points on CA (extended) and draw the triangles with the side BC and the points marked. You will observe that as the length of the side AC is increases (by taking different positions of A), the angle opposite to it, that is ∠B also increases.
[Page No. 169]
![]()
Question 2.
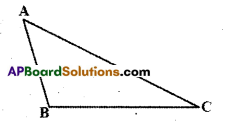
Construct a scalene triangle ABC (that is a triangle in which all sides are of different lengths). Measure the lengths of the sides.

Now, measure the angles. What do you observe?
In ΔABC figure, BC is the longest side and AC is the shortest side. ‘
Also, ∠A is the largest and ∠B is the smallest.
Measure angles and sides of each of the above triangles, what is the rela tion between a side and its opposite angle when compared with another pair?
Activity
Question
Draw a line segment AB. With A as centre and some radius, draw an arc and mark different points say P, Q, R, S, T on it.
Solution:
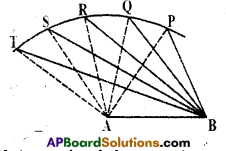
Join each of these points with A as well as with B (see figure). Observe that as we move from P to T, ∠A is becoming larger and larger. What is happening to the length of the side opposite to it? Observe that the length of the side is also increasing; that is ∠TAB > ∠SAB > ∠RAB > ∠QAB > ∠PAB
and TB > SB > RB > QB > PB.
Now, draw any triangle with all angles unequal to each other. Measure the lengths of the sides (see figure).
Observe that the side opposite to the largest angle is the longest. In figure, ZB is the largest angle and AC is the longest side
Repeat this activity for some more triangles and we see that the converse of the above Theorem is also true.
Measure angles and sides of each triangle given below. What relation you can visualize for a side and its opposite angle in each triangle.

In this way, we arrive at the following theorem. [Page No. 170]
![]()
Do This
Question
Draw a triangle ABC and measure its sides. Find the sum of the sides AB + BC, BC + AC; and AC + AB, compare it with the length of the third side. What do you observe ?
[Page No. 171]
Solution:
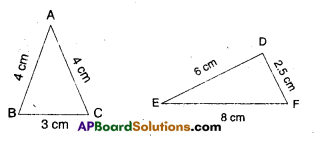
AB + BC = 4 + 3 = 7
= 7 > 4 = AC
BC + CA > AB;
3 + 4 > 4
CA + AB > BC;
4 + 4 > 3
DE + EF > DF
EF + DF > DE
FD + DE > EF
∴ Sum of any two sides of a triangle is greater than the third side.