AP Inter 1st Year Maths 1A Solutions Chapter 3 మాత్రికలు Ex 3(e)

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Chapter 3 మాత్రికలు Exercise 3(e) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1A Solutions Chapter 3 మాత్రికలు Exercise 3(e)

I.

Question 1.
క్రింది మాత్రికల అనుబంధ మాత్రికను విలోమ మాత్రికను కనుక్కోండి.
(i) A = \(\left[\begin{array}{cc}
2 & -3 \\
4 & 6
\end{array}\right]\) [Mar. ’02]
Solution:

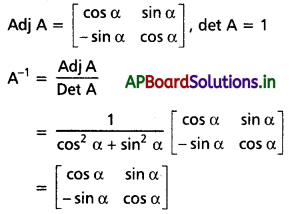
(ii) \(\left[\begin{array}{cc}
\cos \alpha & -\sin \alpha \\
\sin \alpha & \cos \alpha
\end{array}\right]\) [Mar. ’13]
Solution:

(iii) \(\left[\begin{array}{lll}
1 & 0 & 2 \\
2 & 1 & 0 \\
3 & 2 & 1
\end{array}\right]\) [Mar. ’05]
Solution:

(iv) \(\left[\begin{array}{lll}
2 & 1 & 2 \\
1 & 0 & 1 \\
2 & 2 & 1
\end{array}\right]\) [Mar ’08]
Solution:

Question 2.
A = \(\left[\begin{array}{cc}
a+i b & c+i d \\
-c+i d & a-i b
\end{array}\right]\), a² + b² + c² + d² = 1 అయితే, A విలోమం కనుక్కోండి.
Solution:
Det A = (a + ib) (a – ib) – (c + id) (-c + id)
= a² – i²b² – (-c² + i²d²)
= a² + b² + c² + d²
= 1 (∵ i² = -1)

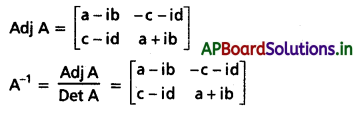
Question 3.
A = \(\left[\begin{array}{ccc}
1 & -2 & 3 \\
0 & -1 & 4 \\
-2 & 2 & 1
\end{array}\right]\) అయితే, (A’)^-1 కనుక్కోండి.
Solution:

Question 4.
A = \(\left|\begin{array}{ccc}
-1 & -2 & -2 \\
2 & 1 & -2 \\
2 & -2 & 1
\end{array}\right|\) అయితే adj A = 3A’ అని చూపి A^-1 కనుక్కోండి.
Solution:

Question 5.
abc ≠ 0, అయితే \(\left[\begin{array}{lll}
\mathbf{a} & \mathbf{0} & \mathbf{0} \\
\mathbf{0} & \mathbf{b} & \mathbf{0} \\
\mathbf{0} & \mathbf{0} & \mathbf{c}
\end{array}\right]\) కు విలోమం కనుక్కోండి. [May ’06]
Solution:

II.

Question 1.
A = \(\left[\begin{array}{lll}
0 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 0
\end{array}\right]\), B = \(\frac{1}{2}\left[\begin{array}{lll}
\mathbf{b}+c & c-a & \mathbf{b}-\mathbf{a} \\
\mathbf{c}-\mathbf{b} & \mathbf{c}+\mathbf{a} & \mathbf{a}-\mathbf{b} \\
\mathbf{b}-\mathbf{c} & \mathbf{a}-c & \mathbf{a}+\mathbf{b}
\end{array}\right]\) అయితే ABA^-1 ఒక వికర్ణ మాత్రిక అని చూపండి.
Solution:
A^-1 ను కనుక్కొందాం

Question 2.
3A = \(\left[\begin{array}{ccc}
1 & 2 & 2 \\
2 & 1 & -2 \\
-2 & 2 & -1
\end{array}\right]\) అయితే A^-1 = A’ అని చూపండి. [Mar. ’14]
Solution:

Question 3.
A = \(\left[\begin{array}{rrr}
3 & -3 & 4 \\
2 & -3 & 4 \\
0 & -1 & 1
\end{array}\right]\) అయితే A^-1 = A³ అని చూపండి.
Solution:

∴ A⁴ = I
det A = 3(1) – 3(-2) + 4(-2) = 1
∵ A ≠ 0 ⇒ A^-1 వ్యవస్థితం
∵ A⁴ = I
A^-1 చే గుణించగా
A⁴ (A^-1) = I (A^-1)
⇒ A³ (A A^-1) = A^-1
⇒ A³ (I) = A^-1
∴ A^-1 = A³

Question 4.
AB = I గానీ, BA = I గానీ అయితే A విలోమనీయ మాత్రిక అనీ B = A^-1 అని నిరూపించండి.
Solution:
AB = I
⇒ |AB| = |I| = |A| |B| = 1
⇒ |A| ≠ 0
∴ A ఒక సాధారణ మాత్రిక
మరియు BA = I
⇒ |BA| = |I|
⇒ |B| |A| = 1
⇒ |A| ≠ 0
∴ A ఒక సాధారణ మాత్రిక
AB = I లేదా BA = I అయితే A విలోమనీయం
∴ A^-1 వ్యవస్థితం
AB = I
⇒ A^-1AB = A^-1I
⇒ IB = A^-1
⇒ B = A^-1
∴ B = A^-1