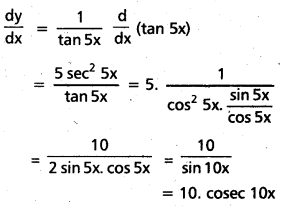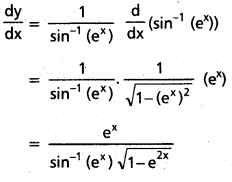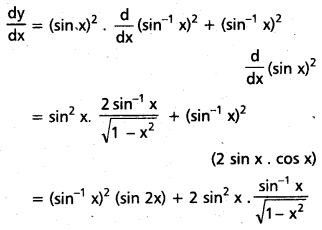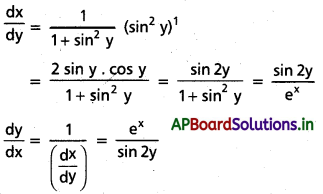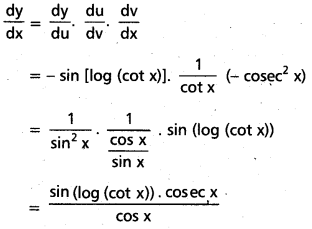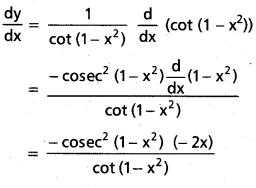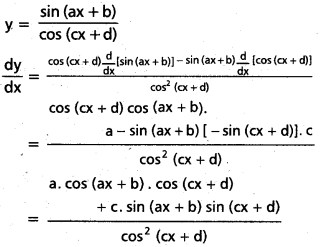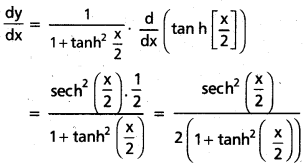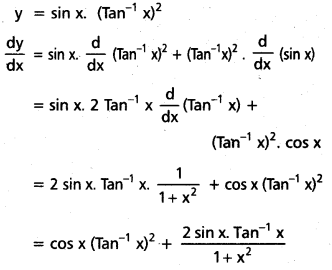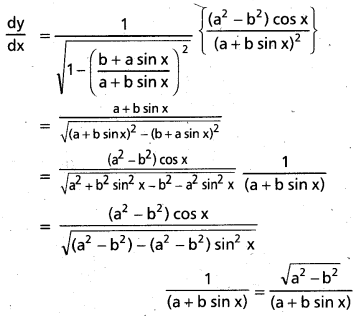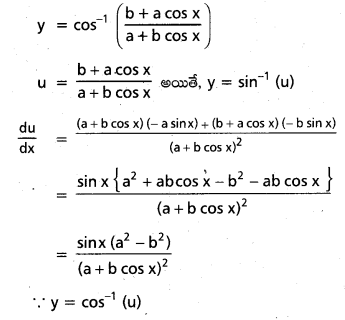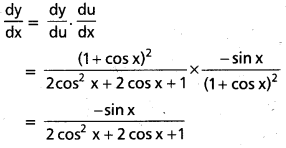Students get through AP Inter 1st Year Maths 1A Important Questions Chapter 7 త్రికోణమితీయ సమీకరణాలు which are most likely to be asked in the exam.
AP Inter 1st Year Maths 1A Important Questions Chapter 7 త్రికోణమితీయ సమీకరణాలు
సాధించిన సమస్యలు
(Solved Problems)
ప్రశ్న 1.
sin x = \(\frac{1}{\sqrt{2}}\)-ని సాధించండి.
సాధన:
sin x = \(\frac{1}{\sqrt{2}}\) = sin \(\frac{\pi}{4}\)
∴ కనుక ప్రధాన సాధన x = \(\frac{\pi}{4}\)
సార్వత్రిక సాధన x = nπ + (-1)n \(\frac{\pi}{4}\), n ∈ Z
ప్రశ్న 2.
sin 2θ = \(\frac{\sqrt{5}-1}{4}\) ‘ని సాధించండి.
సాధన:
sin 2θ = \(\frac{\sqrt{5}-1}{4}\) = sin 18° = sin \(\left(\frac{\pi}{10}\right)\)
\([/latex\left(\frac{\pi}{10}\right)] ∈ [latex]\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\) కనుక
ప్రధాన సాధన
2θ = \(\frac{\pi}{10}\), θ = \(\frac{\pi}{20}\)
సార్వత్రిక సాధన
2θ = nπ + (-1)n\(\frac{\pi}{10}\), n ∈ Z (లేదా)
θ = n\(\frac{\pi}{2}\) + (-1)n\(\frac{\pi}{20}\), n ∈ Z
ప్రశ్న 3.
tan2 θ = 3 ని సాధించండి.
సాధన:
tan2 θ = 3 ⇒ tan θ = ±\(\sqrt{3}\) = tan \(\left(\pm \frac{\pi}{3}\right)\), ± \(\frac{\pi}{3}\) ∈ \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\)
∴ ప్రధాన సాధనలు θ = ±\(\frac{\pi}{3}\)
సార్వత్రిక సాధన nπ ± \(\frac{\pi}{3}\), n ∈ Z
![]()
ప్రశ్న 4.
3 cosec x = 4 sin x ని సాధించండి.
సాధన:
3 cosec x = 4 sin x
⇔ \(\frac{3}{\sin x}\) = 4 sin x
⇒ sin2 x = \(\frac{3}{4}\)
⇔ sin x = ± \(\frac{\sqrt{3}}{2}\)
∴ ప్రధాన సాధనలు x = ± \(\frac{\pi}{3}\)
సార్వత్రిక సాధన
x = nπ ± \(\frac{\pi}{3}\), n ∈ Z
ప్రశ్న 5.
x ఒక లఘుకోణం, sin(x + 10°) = cos(3x – 68°) అయితే x విలువ కనుక్కోండి
సాధన:
sin (x + 10°) = cos (3x – 68°)
⇔ sin(x + 10°) = sin (90° + 3x – 68°)
= sin (22° + 3x)
∴ x + 10° = n(180°) + (-1)n (22° + 3x)
n = 2k, k ∈ Z అయితే
x + 10° = (2k) (180°) + (22° + 3x)
⇒ 2x = -k(360°) – 12°
⇒ x = \(\frac{-k\left(360^{\circ}\right)-12^{\circ}}{2}\)
= -k(180°) – 6°
ఇది అసంభవం. ఎందుకంటే ఏ పూర్ణాంకం k తీసుకొన్నా,
x అల్పకోణం కాదు.
n = 2k + 1, అయితే
x + 10° = (2k + 1) 180° – (22° + 3x)
⇒ 4x = (2k + 1) 180° – 32°
⇒ x = (2k + 1) 45° – 8°
k = 0 ⇒ x = 37°
k కి ఇతర పూర్ణాంకాలు ఇచ్చినప్పుడు x అల్పకోణం కాదు.
∴ x = 37° మాత్రమే దత్త సమీకరణానికి సాధన.
ప్రశ్న 6.
cos 3θ = sin 2θ ని సాధించండి.
సాధన:
cos 3θ = sin 2θ = cos(\(\frac{\pi}{2}\) – 2θ)
⇒ 3θ = 2nπ ± (\(\frac{\pi}{2}\) – 2θ), n ∈ Z
⇒ 3θ = 2nπ + (\(\frac{\pi}{2}\) – 2θ) (లేదా)
3θ = 2nπ + \(\frac{\pi}{2}\) (లేదా) θ = 2nπ – \(\frac{\pi}{2}\)
⇒ θ = (4n + 1) \(\frac{\pi}{10}\), n ∈ Z (లేదా)
θ = (4n – 1) \(\frac{\pi}{2}\), n ∈ Z
ప్రశ్న 7.
sin2θ + 3 cos2θ = 4 ని సాధించండి.
సాధన:
7 sin2θ + 3 cos2θ = 4
⇒ 7 sin2θ + 3(1 – sin2θ) = 4
⇒ 4 sin2θ = 1
⇒ sin θ = ± \(\frac{1}{2}\)
∴ ప్రధాన సాధనాలు θ = ±\(\frac{\pi}{6}\)
సార్వత్రిక సాధన
θ = nπ ± \(\frac{\pi}{6}\), n ∈ Z
ప్రశ్న 8.
2 cos2θ – \(\sqrt{3}\) sin θ + 1 = 0 ని సాధించండి.
సాధన:
2 cos2θ – \(\sqrt{3}\) sin θ + 1 = 0
⇒ 2(1 – sin2θ) – \(\sqrt{3}\) sin θ + 1 = 0
⇒ 2 sin2θ + \(\sqrt{3}\) sin θ – 3 = 0
⇒ (2 sin θ – \(\sqrt{3}\)) (sin θ + \(\sqrt{3}\)) = 0
⇒ sin θ = \(\frac{\sqrt{3}}{2}\) = sin \(\left(\frac{\pi}{3}\right)\)
∴ ప్రధాన సాధన θ = \(\frac{\pi}{3}\)
సార్వత్రిక సాధన
θ = nπ + (-1)n \(\frac{\pi}{3}\), n ∈ Z
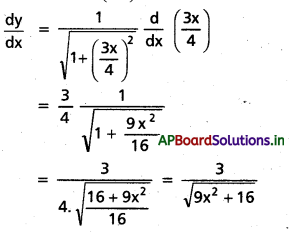
![]()
ప్రశ్న 9.
(-π, π) అంతరంలో 81 + cos x + cos2 x + ……. = 43 సమీకరణాన్ని తృప్తిపరిచే x యొక్క శూన్యేతర విలువలను కనుక్కోండి.
సాధన:
cos x = ±1,
అయితే 1 + cos x + cos2 x + ……… ∞
అభిసరణ చెందదు | cos x | < 1 అనుకుందాం
అప్పుడు 1 + cos x + cos2 x + ….. ∞
= \(\frac{1}{1-\cos x}\)
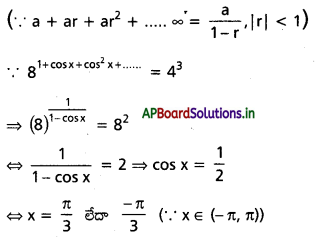
ప్రశ్న 10.
tan θ + 3 cot θ = 5 sec θ సాధించండి.
సాధన:
tan θ + 3 cot θ = 5 sec θ దత్త సమీకరణ౦
cos θ ≠ 0, sin θ ≠ 0 అయినప్పుడు మాత్రమే సాధికార మవుతుంది
⇒ \(\frac{\sin \theta}{\cos \theta}\) + 3 \(\frac{\cos \theta}{\sin \theta}\) = \(\frac{5}{\cos \theta}\)
⇒ sin2 θ + 3 cos2 θ = 5 sin θ
⇒ sin2 θ + 3(1 -sin2 θ) – 5 sin θ = 0
⇒ 2sin2θ + 5 sin θ – 3 = 0
⇒ 2sin2θ + 6 sin θ – sin θ – 3 = 0
⇒ 2 sin θ (sin θ + 3) – 1 (sin θ + 3) = 0
⇒ (2 sin θ – 1) (sin θ + 3) = 0
⇒ sin θ = \(\frac{1}{2}\) (∵ sin θ ≠ -3)
∴ sin θ = \(\frac{1}{2}\) = sin \(\left(\frac{\pi}{6}\right)\)
∴ ప్రధాన సాధన θ = \(\frac{\pi}{6}\)
సార్వత్రిక సాధన θ = nπ + (−1)n \(\frac{\pi}{6}\) = nπ + (-1)n\(\frac{\pi}{6}\), n ∈ Z
![]()
ప్రశ్న 11.
1 + sin2 θ = 3 sin θ cos θను సాధించండి. (Mar. 11)
సాధన:
1 + sin2 θ = 3 sin θ cos θ
cosθ, చే భాగించగా
sec2 θ + tan2 θ = 3 tan θ
⇒ (1 + tan2 θ) + tan2 θ – 3 tan θ = 0
⇒ 2 tan2 θ – 3 tan θ + 1 = 0
⇒ 2 tan2 θ – 2 tan θ – tan θ + 1 = 0
⇒ 2 tan θ(tan θ – 1) – (tan θ – 1) = 0
⇒ (tan θ – 1) (2 tan θ – 1) = o
∴ tan θ = 1 (లేదా) tan θ = \(\frac{1}{2}\)
ఇప్పుడు tan θ = 1 = tan \(\frac{\pi}{4}\)
∴ ప్రధాన సాధన θ = \(\frac{\pi}{4}\)
సార్వత్రిక సాధన
θ = nπ + \(\frac{\pi}{4}\), n ∈ Z
tan θ = \(\frac{1}{2}\) కి α ప్రధాన సాధన అనుకుంటే సార్వత్రిక సాధన θ = nπ + α, n ∈ Z అవుతుంది.
ప్రశ్న 12.
\(\sqrt{2}\)(sin x + cos x) = \(\sqrt{3}\) సాధించండి. (A.P.)(Mar. 15; May 11, 08)
సాధన:
\(\sqrt{2}\)(sin x + cos x) = \(\sqrt{3}\)
⇔ sin x + cos x = \(\sqrt{\frac{3}{2}}\)
ఇరువైపుల \(\sqrt{2}\) చే భాగించగా
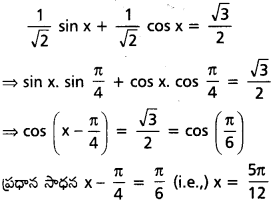
సార్వత్రిక సాధన
x – \(\frac{\pi}{4}\) = 2nπ ± \(\frac{\pi}{6}\), n ∈ Z
ప్రశ్న 13.
sin θ = \(-\frac{1}{2}\), cos θ = \(-\frac{\sqrt{3}}{2}\) సమీకరణాలను రెండింటిని తృప్తిపరచే θ కు, సార్వత్రిక విలువను
కనుక్కోండి.
సాధన:
sin θ = \(-\frac{1}{2}\) = -sin \(\frac{\pi}{6}\)
= sin(π + \(\frac{\pi}{6}\)) లేదా sin (2π – \(\frac{\pi}{6}\))
= sin \(\frac{7 \pi}{6}\) లేదా \(\frac{11 \pi}{6}\)
∴ (0, 2π) లో θ sinθ = \(-\frac{1}{2}\) ను తృప్తిపరచే కోణాలు
\(\frac{7 \pi}{6}\) లేదా \(\frac{11 \pi}{6}\)
cos θ = \(-\frac{\sqrt{3}}{2}\) = -cos\(\frac{\pi}{6}\)
= cos (π – \(\frac{\pi}{6}\)) లేదా cos (π + \(\frac{\pi}{6}\) )
= cos \(\frac{5 \pi}{6}\) లేదా cos \(\frac{7 \pi}{6}\)
∴ (0, 2π) లో cos θ = \(-\frac{\sqrt{3}}{2}\) ను తృప్తిపరచే కోణాలు \(\frac{5 \pi}{6}\) లేదా \(\frac{7 \pi}{6}\)
కనుక \(\frac{7 \pi}{6}\) కోణం మాత్రమే రెండు సమీకరణాలను తృప్తిపరుస్తుంది.
కనుక θ కి సార్వత్రిక విలువ θ = 2nπ + \(\frac{7 \pi}{6}\), n ∈ Z.
ప్రశ్న 14.
a cos 2θ + b sin 2θ = c సమీకరణానికి θ1, θ2 లు సాధనలు, tan θ1 ≠ tan θ2, a + c ≠ 0, అయితే
(i) tan θ1 + tan θ2
(ii) tan θ1. tan θ2 విలువలు కనుక్కోండి. (T.S) (Mar. ’15)
సాధన:
a cos 2θ + b sin 2θ = c
⇔ a\(\left(\frac{1-\tan ^2 \theta}{1+\tan ^2 \theta}\right)\) + b\(\left(\frac{2 \tan \theta}{1+\tan ^2 \theta}\right)\) = c
⇔ a – a tan2 θ + 2b tan θ = c + c tan2 θ
⇔ a – a tan2θ + 2b tan θ = c + c tan2θ
⇔ (a + c) tan2θ – 2b tan θ + (c – a) = 0 ——- (1)
ఇది tan θ లో వర్గ సమీకరణం.
θ1, θ2 లు దత్త సమీకరణానికి మూలాలు కనుక tan θ1, tan θ2 లు సమీకరణం (1) కి మూలాలు అవుతాయి.
∴ మూలాల మొత్తం = \(\frac{2 b}{a+c}\)
అంటే tan θ1 + tan θ2 = \(\frac{2 b}{a+c}\)
మూలాల లబ్దం = tan θ1, tan θ2 = \(\frac{c-a}{c+a}\)
ఇప్పుడు tan (θ1 + θ2) = \(\frac{\tan \theta_1+\tan \theta_2}{1-\tan \theta_1 \tan \theta_2}\)
= \(\frac{\left(\frac{2 b}{a+c}\right)}{1-\left(\frac{c-a}{c+a}\right)}\) = \(\frac{2 b}{2 a}\) = \(\frac{b}{a}\)
![]()
ప్రశ్న 15.
4 sin x sin 2x sin 4x = sin 3x సాధించండి. (Mar. 13)
సాధన:
sin 3x = 4 sin x sin 2x sin 4x
= 2 sin x (2 sin 4x sin 2x)
= 2 sin x [cos (2x) – cos 6x]
⇔ sin 3x = 2 cos 2x sin x − 2 cos 6x sin x
⇔ sin 3x = sin (3x) – sin x – 2 cos 6x sin x
⇒ 2 cos 6x sin x + sin x = 0
⇒ sin x (2 cos 6x + 1) = 0
⇒ sin x = 0 (లేదా) cos 6x = \(\frac{-1}{2}\)
సంధర్భ౦ (i): sin x = 0
⇒ ప్రధాన సాధన x = 0
సార్వత్రిక సాధన x = nπ, n ∈ Z
సంధర్భ౦ (ii): cos 6x = \(\frac{-1}{2}\) = cos \(\left(\frac{2 \pi}{3}\right)\)
ప్రధాన సాధన
6x = \(\frac{2 \pi}{3}\) ⇒ x = \(\frac{\pi}{9}\) సార్వత్రిక సాధన
6x = 2nπ ± \(\frac{2 \pi}{3}\), n ∈ Z
⇒ x = \(\frac{n \pi}{3}\) ± \(\frac{\pi}{9}\), n ∈ Z
ప్రశ్న 16.
0 < θ < π అయితే cos θ. cos 2θ cos 3θ = \(\frac{1}{4}\) సాధించండి.
సాధన:
4 cos θ cos 2θ cos 3θ = 1
⇒ 2 cos 2θ (2 cos 3θ. cos θ) = 1
⇒ 2 cos 2θ (cos 4θ + cos 2θ) = 1
⇒ 2 cos 4θ cos 2θ+ (2 cos2 2θ – 1) = 0
⇒ 2 cos 4θ cos 2θ + cos 4θ = 0
⇒ cos 4θ (2 cos 2θ + 1) = 0
⇒ cos 4θ = 0 (లేదా) cos 2θ = \(\frac{-1}{2}\)
సందర్భ౦ (i) : cos 4θ = 0 = cos \(\left(\frac{\pi}{2}\right)\)
ప్రధాన సాధన
⇒ 4θ = \(\frac{\pi}{2}\) లేదా θ = \(\frac{\pi}{8}\)
సార్వత్రిక సాధన
4θ = (2n + 1)\(\frac{\pi}{8}\), n ∈ Z
⇒ θ = (2n + 1)\(\frac{\pi}{8}\), n ∈ Z
n = 0, 1, 2, …… రాస్తే
{\(\frac{\pi}{8}\), \(\frac{3 \pi}{8}\), \(\frac{5 \pi}{8}\), \(\frac{7 \pi}{8}\)}
విలువలు (0, π) అంతరంలో సాధనలు అవుతాయి.
సందర్భ౦ (ii): cos 2θ = \(\frac{-1}{2}\) = cos \(\left(\frac{2 \pi}{3}\right)\)
ప్రధాన సాధన
⇒ 2θ = \(\frac{2 \pi}{3}\) (లేదా) θ = \(\frac{\pi}{3}\)
సార్వత్రిక సాధన
2θ = 2nπ ± \(\frac{2 \pi}{3}\), n ∈ Z
⇒ θ = nπ ± \(\frac{\pi}{3}\), n ∈ Z
n = 0, 1, తీసుకొంటే \(\left\{\frac{\pi}{3}, \frac{2 \pi}{3}\right\}\) లు (0, π) అంతరంలో సాధనలు అవుతాయి.
దత్త సమీకరణానికి (0, π) అంతరంలో సాధనలు
{\(\frac{\pi}{8}\), \(\frac{\pi}{3}\), \(\frac{3 \pi}{8}\), \(\frac{5 \pi}{8}\), \(\frac{2 \pi}{8}\), \(\frac{7 \pi}{8}\)}
ప్రశ్న 17.
p ≠ ±q, cos pθ + cos qθ = 0 సమీకరణ సాధనలు రెండు అంకశ్రేఢులు అవుతాయని చూపి వాటి పదాంతరాన్ని కనుక్కోండి.
సాధన:
cos pθ + cos qθ = 0

ఇది ఒక అంకశ్రేఢి. దీని పదాంతరం \(\frac{2 \pi}{(p+q)}\). ఇదే విధంగా
cos \(\left(\frac{p-q}{2}\right) \theta\) = 0 కి సాధనలు
θ = \(-\frac{\pi}{p-q}\), \(\frac{\pi}{p-q}\), \(\frac{3 \pi}{p-q}\), \(\frac{5 \pi}{p-q}\)……..
ఇది మరొక అంకశ్రేఢి. దీని పదాంతరం \(\frac{2 \pi}{(p-q)}\)
![]()
ప్రశ్న 18.
sin 2x – cos 2x = sin x – cos x సాధించండి.
సాధన:
(sin 2x – sin x) – (cos 2x – cos x) = 0

∴ దత్త సమీకరణానికి సాధన సమితి
{2nπ/ n ∈ Z} ∪ {\(\frac{2 n \pi}{3}\) – \(\frac{\pi}{6}\)/n ∈ Z}